Дифференциальное исчисление функции многих переменных

Пример 1. Найти частные производные функции двух переменныхz=2x² +sin y.

Рассматривая yкак постоянный параметр, а следовательно иsiny=const, и производная от нее равна нулю, получим

При вычислении производной по y переменнуюxсчитаем постоянной, в результате получим

Пример 2. Найти частные производные функции трех переменныхz(x,y,t)=x² y +t cos y + sin (t²+3).

При вычислении производной по xбудем считать, что переменныеy иt постоянны. Тогда производные от двух последних слагаемых равны нулю, а в первом параметрy выступает как постоянный множитель. В результате получим

Полагая переменные xи tпостоянными, найдем производную по переменнойy.

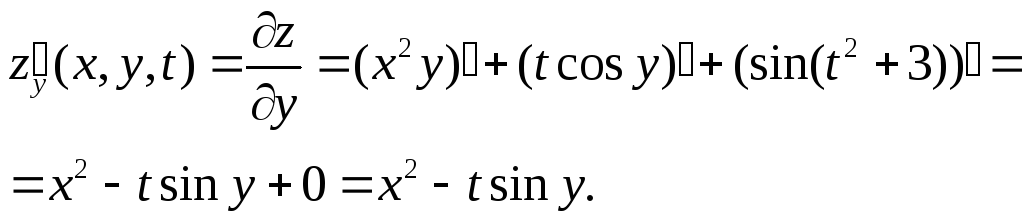
При вычислении производной учитывалось, что в первых двух слагаемых x² иt выступают в качестве постоянных множителей.

Аналогично вычислим производную по переменной t.

Пример 3. Найти частные производные функции двух переменныхz(x,y)=e^x/y.

Полагая поочередноy=const,x=const, найдем частные производные

Задания для самостоятельной работы

Пример. Найти частные производные функций многих переменныхz=f(x₁, x₂, x₃,… x_n):

Полный дифференциал

Пример 1. Найти полный дифференциал функции двух переменных

z(x,y)=tg(x/y).

Найдем сначала частные производные по переменным x иy.

Согласно формуле для полного дифференциала запишем

Пример 2. Найти полный дифференциал функции трех переменных

z(x,y,t)=xsin yt+ysin xt+tsin xy.

Найдем все частные производные:

Тогда, соответственно, для dz получим

Задания для самостоятельной работы

Пример. Найти полный дифференциал функций многих переменныхz=f(x₁, x₂, x₃,… x_n):

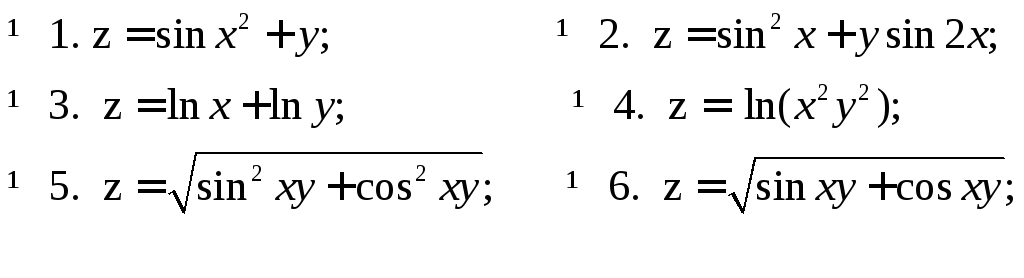
Частные производные сложных функций

Пример 1. Найти производную сложной функцииz=e^x+e^y, гдеx=sin t, y= cos t.

Вычислим все необходимые производные

Для производной сложной функции получим

Подставив вместо переменных xи y их выражения черезt, окончательно запишем

Пример 2. Найти производную сложной функцииz=xּlny, гдеx=p/q, y = p-q.

Вычислим частные производные

Подставив в формулу для вычисления производных, и заменив xиyчерезpиqполучим

Задания для самостоятельной работы

Производные высших порядков

Форма контроля: Проверка решений задач и заданий

Дифференциальные уравнения

Примеры решения дифференциальных уравнений.

1) Найтиобщее решение дифференциального уравненияи частное решение, удовлетворяющее начальному условию

Решение

Данное дифференциальное уравнение является дифференциальным уравнением с разделяющимися переменными.

Сделаем преобразования:

Записали уравнение так, чтобы при дифференциале dy был множитель, зависящий только отy, а при дифференциалеdxбыл множитель, зависящий только отx.

Далее проинтегрируем обе части полученного равенства

или.

Окончательно получим общее решение дифференциального уравнения:

Найдём частное решение, используя начальное условие .

Найдём значение постоянной интегрирования С

.

Запишем частное решение дифференциального уравнения при данных начальных условиях:

2) Найтиобщее решение дифференциального уравнения

tg=и частное решение, удовлетворяющее начальному условиюy(0)=2.

Решение

Данное уравнение является линейным, так как содержит искомую функцию yи её производнуюв первой степени и не содержит их произведений.

Применяем подстановку y=uv, гдеuиv- некоторые неизвестные функции аргументаx, тогда(uvu^'_*v+u v^', и данное уравнение принимает вид:u^'v+uv^'-uvtg=илиv (u^'-u tg)+uv^'=(1)

Так как искомая функция упредставлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функциюuтак, чтобы выражение, стоящее в круглых скобках левой части последнего равенства(1), обращалось в нуль, т.е. чтобы имело место равенствоu^'-utgx=0 (2).

Тогда уравнение (1) примет вид: uv^'=(3).

Уравнение (2) является уравнением с разделяющимися переменными относительно uиx. Решим его:

- = 0= =

==

=-ln u=

Чтобы равенство (2) имело место, достаточно найти одно какое-либо решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной (с=0). Подставив в (3) найденное выражение для uполучим: v^'=2v^'=2=

Интегрируя, получаем v=. Тогдаесть общее решение данного дифференциального уравнения.

Определим численное значение С при указанных начальных условиях. Имеем: 2=Следовательно,C=2.

Таким образом, есть частное решение, удовлетворяющее заданному начальному условию.