Игры с “природой”

Задача 3. Торговое предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей. Получаемая от их возможных сочетаний величина прибыли представлена в виде матрицы выигрышей в следующей таблице (смысл величиныбудет объяснен позже):

= 0,6

План продажи	Состояние конъюнктуры рынка и спроса
	150	150	150	150
	100	300	300	300
	50	250	450	450
	0	200	400	600

Определить оптимальный план продажи товаров.

Решение.Задачи такого типа относятся киграм с “природой”. Любую хозяйственную деятельность человека можно рассматривать как игру с “природой”. Под “природой” понимается совокупность неопределенных факторов, влияющих на эффективность принимаемых решений. Иногда при этом имеются некоторые вероятностные характеристики состояний “природы”.

Игра с “природой” отличается от матричной игры, в которой принимают участие два сознательных игрока, безразличием “природы” к выигрышу. “Природа” может даже помогать игроку. Такие игры в основном бывают двух типов: когда вероятности состояний “природы” неизвестны и когда они известны.

Для решения игры с “природой” был предложен ряд критериев, ни один из которых не является универсальным, поскольку каждый из них основывается на своих допущениях. Для выбора наилучшего решения следует использовать тот критерий, который в большей степени отвечает субъективному понятию риска конкретного игрока. Другой подход заключается в применении по очереди всех критериев, причем каждый критерий дает свою рекомендацию относительно того, какое решение игрока является наилучшим. Если одна из стратегий (решений) игрока фигурирует в качестве лучшей чаще других, она в результате признается оптимальной.

1 случай. Вероятности состояний “природы”неизвестны.

Максиминный критерий Вальда. С точки зрения этого критерия, игра с “природой” ведётся как игра с разумным, агрессивным противником, который всегда реализует самое невыгодное для игрока состояние. Это крайне пессимистический критерий. Здесь нужно рассчитывать на самый наихудший вариант, и поэтому при любой стратегии игрока ожидается, что выигрыш будет наименьшим. Поэтому из этих наименьших выигрышей по каждой стратегии выбирается наибольшее значение, которое гарантирует игроку хотя бы наименьший возможный выигрыш:

, (1)

где а_ij– элемент матрицы выигрышей.

Сначала из каждой строки матрицы выбираем минимальный элемент, а затем среди полученных значений выбираем максимальное. Таким образом, получаем:

W = 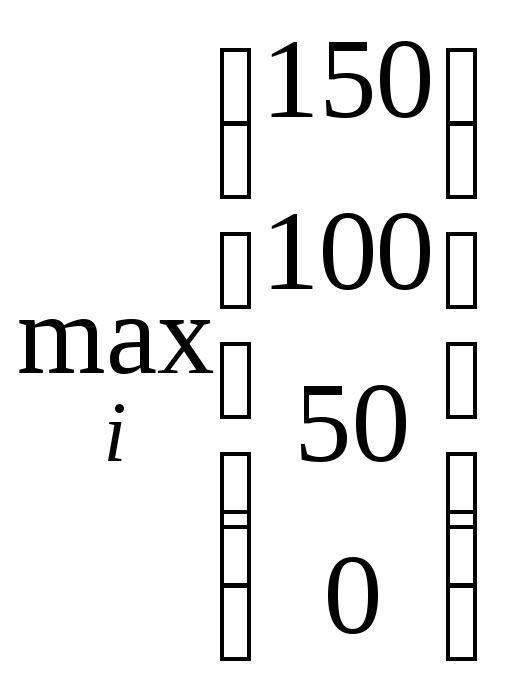= 150,

что соответствует стратегии. Таким образом, согласно критерию Вальда, наилучшей является стратегия, гарантирующая выигрыш, равный 150.

Критерий минимального риска Сэвиджа.Это также крайне пессимистический критерий, однако, в отличие от критерия Вальда, ориентируется не на выигрыш, а на риск проигрыша:

,(2)

где r_ij– элемент матрицы рисков.

Матрица рисков имеет ту же размерность, что и матрица выигрышей, и формируется по столбцам матрицы выигрышей. Элементы её го столбца получаются из матрицы выигрышей по формуле:

r_ij =,

где =- максимальный элементго столбца матрицы выигрышей.

Таким образом, в данной задаче получаем:

и матрица рисков имеет вид:

.

Теперь применяем формулу (2):

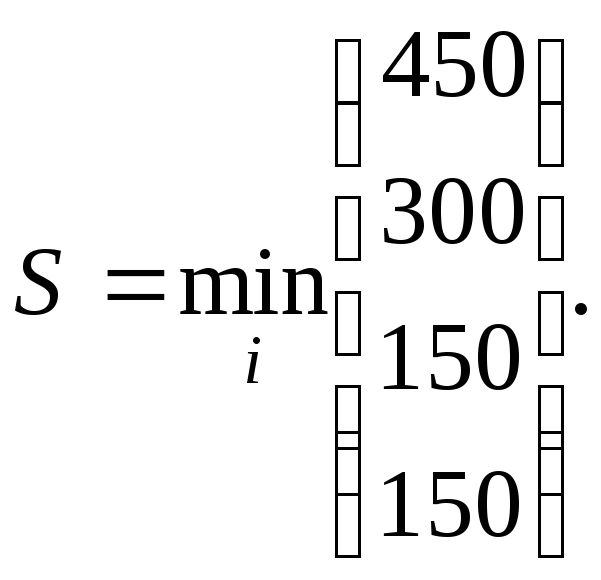
Как видим, минимум дают сразу две стратегии - и, которые и являются наилучшими с точки зрения критерия Сэвиджа.

Критерий пессимизма-оптимизма Гурвица. Согласно этому критерию оптимальной считается стратегия, определяемая из соотношения:

, (3)

где– коэффициент пессимизма, который принимает значения в диапазоне:.

В случае, когда , получается критерий Вальда, т.е. крайний пессимизм. При возникает ситуация крайнего оптимизма, когда в матрице выигрышей по формуле (3) отыскивается самый большой элемент. Обычно принимают, и конкретное значение коэффициента задается из субъективных соображений. Здесь в условиях задачи указано = 0,6. Применим формулу (3):

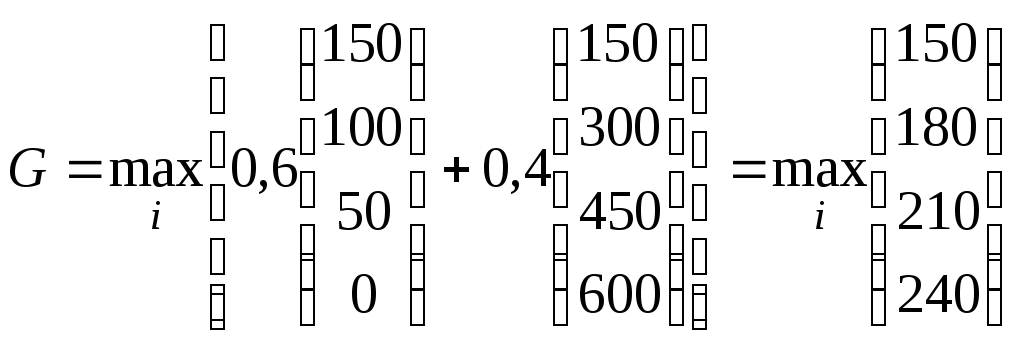=240.

Согласно критерию Гурвица, оптимальной следует считать стратегию. Как видим, эта стратегия появляется в качестве оптимальной второй раз.

Критерий максимума математического ожидания выигрыша.Поскольку вероятности состояний природы нам неизвестны, принимаем все состояния равновероятными, т.е..

Отсюда средний выигрыш от применения i–й стратегии находим по формуле:

,. (4)

Для нашего случая:

М₁=¼ ( 150 + 150 + 150 + 150) = 150;

М₂=¼ ( 100 + 300 + 300 + 300) = 250;

М₃=¼ ( 50 + 250 + 450 + 450 ) = 300;

М₄=¼ ( 0 + 200 + 400 + 600 ) = 300.

Среди этих средних выигрышей выбираем максимальный:

=М₃=М₄= 300.

Имеем две оптимальные стратегии - и_.

Критерий минимального среднего риска. Решение по этому критерию эквивалентно решению по предыдущему критерию, однако анализу подвергается матрица рисков:

. (5)

Из этих средних значений рисков выбираем наименьшее.

Применив формулу (5), получим:

R₁=¼ ( 0 + 150 + 300 + 450 ) = 225; R₂=¼ ( 50 + 0 + 150 + 300 ) = 125;

R₃=¼ ( 100 + 50 + 0 + 150 ) = 75; R₄=¼ ( 150 + 100 + 50 + 0 ) = 75.

Отсюда =R₃=R₄= 75. Здесь также имеем две оптимальные стратегии -и_.

Таким образом, по совокупности критериев наилучшей следует принять стратегию. Это и есть решение задания.

2 случай. Вероятности состояний “природы” известны.

Вновь рассмотрим приведенное выше задание, но с известными вероятностями состояний “природы”, указанными в последней строке таблицы:

План продажи	Состояние конъюнктуры рынка и спроса
	150	150	150	150
	100	300	300	300
	50	250	450	450
	0	200	400	600
	0,3	0,2	0,4	0,1

Выполнение задания в этих вариантах имеет следующие особенности:

1. Применение критериев Вальда, Гурвица и Сэвиджа не отличается от прежнего случая.

2. Формулы (4), (5) примут следующий вид:

(или), (6)

(или). (7)

Таким образом, для рассматриваемых исходных условий задачи 2-го случая имеем:

М₁ = 1500,3 + 1500,2 + 1500,4 + 1500,1 = 150,

М₂ = 1000,3 + 3000,2 + 3000,4 + 3000,1 = 240,

М₃ = 500,3 + 2500,2 + 4500,4 + 4500,1 = 290,

М₄ = 00,3 + 2000,2 + 4000,4 + 6000,1 = 260.

По критерию максимума математического ожидания выигрыша находим:

,

что соответствует наилучшей стратегии А₃.

Определим средние риски для разных планов продаж:

R₁ = 00,3 + 1500,2 + 3000,4 + 4500,1 = 195,

R₂ = 500,3 + 00,2 + 1500,4 + 3000,1 = 105,

R₃ = 1000,3 + 500,2 + 00,4 + 1500,1 = 55,

R₄ =1500,3 + 1000,2 + 500,4 + 00,1 = 85.

Отсюда

,

что также соответствует наилучшей стратегии А₃.

По совокупности критериев в данном случае оптимальной следует принять стратегию А₃.