1. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (большие независимые выборки объемов ).

Пример 1.:Из двух партий сахарной свеклы взяты выборки объемомкг икг клубней. Сахаристость первой партии, второй. Установлено, что сахаристости в обеих партиях есть нормальные случайные величины с дисперсиями,.

При уровне значимости проверить нулевую гипотезупри конкурирующей гипотезе.

Можно ли считать, что разброс выборочных средних не случаен?

Решение: Находим

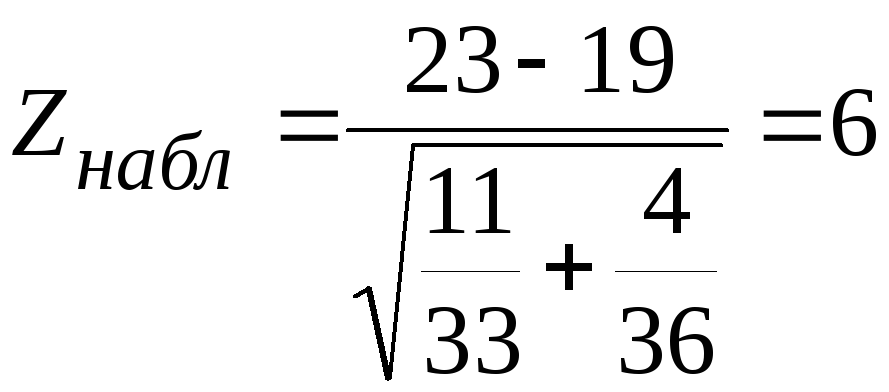
Так как конкурирующая гипотеза имеет вид , то критическая область двусторонняя симметричная.

Критическую точку находим из равенства

Полученные результаты изображены на числовой оси

-2,58 0 2,58 6

Т.к. попадает в критическую область, нулевую гипотезу отвергаем.

Сахаристость свеклы в двух партиях отличается значимо.

2. Сравнение двух дисперсий нормальных генеральных совокупностей..

Пример 2.Из двух нормально распределенных генеральных совокупностейивзяты выборки объемов,. Найдены исправленные выборочные дисперсии,. При уровне значимостипроверить нулевую гипотезупри конкурирующей.

Решение:Находим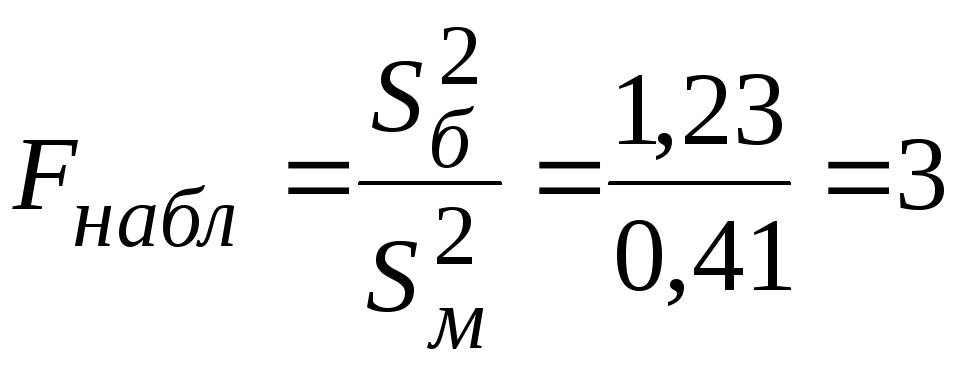

Так как конкурирующая гипотеза имеет вид , то критическая область двусторонняя симметричная.

Критическую точку находим из таблицы распределения Фишера-Снедекора

,;

Так как , то нулевую гипотезу отвергаем, то есть выборочные дисперсии отличаются значимо (существенно).

3.Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности (сравнение со стандартом а).

А) Дисперсия генеральной совокупности известна.

Пример 3.Обследовано 46 случайно отобранных деталей. Средний вес составилг. Считая, что вес деталей распределен нормально, проверить нулевую гипотезуг при конкурирующей гипотезе. Генеральная дисперсия. Уровень значимости. Действительно ли средний вес деталей удовлетворяет стандартуг.

Решение:Так каккритическая область двусторонняя симметричная. Находим критическую точку

По таблице функции Лапласа

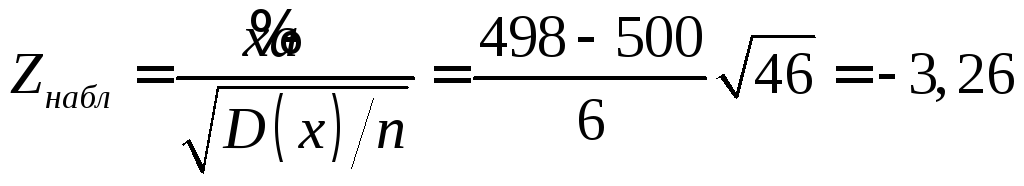
Так как - нулевую гипотезу отвергаем. Средний вес деталейне удовлетворяет стандарту.

Б) Дисперсия генеральной совокупности неизвестна.

Пример 4. Обследованослучайно отобранных деталей по весу. Средний вес детали составилг. Исправленное выборочное среднеквадратическое отклонение 4. считая, что вес деталей распределен нормально, проверить нулевую гипотезуг при конкурирующейг. Уровень значимости. Действительно ли средний вес деталей удовлетворяет стандартуг?

Решение:Вычислим наблюдаемое значение критерия.

Так как конкурирующая гипотеза имеет вид критическая область двусторонняя. По таблице критических точек распределения Стьюдента по уровню значимости, помещенному в верхней строке таблицы и по числу степеней свободынаходим,

. Отсюда следует: нулевая гипотеза отвергается, средний вес не соответствует стандарту.

Пример 5. По выборке объеманайдены выборочная средняяи исправленное среднеквадратическое отклонение. Уровень значимости. Проверить нулевую гипотезупри конкурирующей.

Решение:Вычислим наблюдаемое значение критерия.

Так как конкурирующая гипотеза имеет вид критическая область левосторонняя. По таблице критических точек распределения Стьюдента по уровню значимости, помещенному в нижней строке таблицы и по числу степеней свободынаходим.

Следовательно, ,

Нулевую гипотезу принимаем.