Тема. Законы распределения случайных величин
1. Нормальное распределение
Пример 1.Вес вылавливаемых в пруду рыб подчиняется нормальному закону с математическим ожиданием, равным 375 г, и средним квадратическим отклонением 25 г. Определить вероятность того, что вес одной пойманной рыбы будет заключен в пределах от 300 до 400г.
Решение.
Дано: М(Х)=а=375 г.,
г.,
с=300г.,d=400г.
Найдем искомую вероятность.
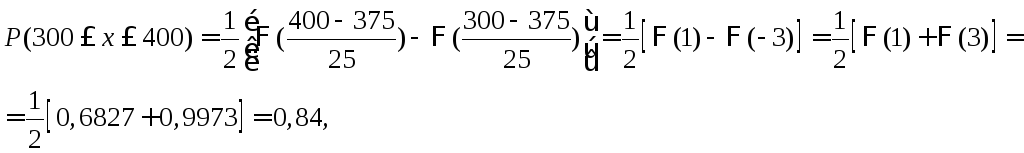
где функции Лапласа Ф(1) = 0,6827, Ф(3) = 0,9973.
Пример 2. Ошибка измерения прибора подчиняется нормальному распределению. С вероятностью 0,92 ошибка измерения не превосходит 4. Найти среднее квадратическое отклонение ошибки прибора. Систематическая ошибка отсутствует.
Решение.
Дано:
,
Воспользовавшись второй теоремой о
нормальной случайной величине, найдем
величину
.
Из таблицы Лапласа, зная
, найдемt=1,75.
Тогда
или
Ответ:
.
2. Равномерное распределение
Пример 3. Цена деления шкалы прибора 0,5 вольт. При измерениях показания округляются до ближайшего целого деления. Найти вероятность того, что при считывании показаний будет сделана ошибка, не превышающая 0,01 вольт.
Решение.
Дано: Случайная величина Х -- истинное
показание прибора имен равномерное
распределение с параметрами а=0 ,в=0,5. Тогда
.
Искомая вероятность – это вероятность
показания х либо на
,
либо на
.
Задания для самостоятельной работы
1) Размер детали подчиняется нормальному закону распределения со средней арифметической 15 мм и дисперсией 0,25. Определить ожидаемый процент брака, если допустимые размеры находятся в пределах от 14 мм до 17 мм. Найти выражение интегральной и дифференциальной функции.
2) Изготовленные цехом детали по размерам диаметра распределяются по нормальному закону с математическим ожиданием, равным 4,5 см, и средним квадратическим отклонением 0,5 см. Определить вероятность того, что размер диаметра наудачу взятой детали отклонится от математического ожидания не более, чем на 1 см.
3) Математическое ожидание нормально распределенной случайной величины равно 15, среднее квадратическое отклонение равно 5. Определить вероятность того, что абсолютная величина отклонения Х-М(Х) будет меньше 10.
4) Ошибка измерения – нормально распределенная случайная величина с дисперсией, равной 100. Систематическая ошибка отсутствует. Найти вероятность того, что ошибка измерения окажется в интервале (3;6).
5) Ошибка взвешивания – случайная нормально распределенная величина с дисперсией 400. Весы заранее настроены на обвес 50 г. Найти вероятность того, что ошибка взвешивания находится в пределах от 30 до 70 г.
6) Автобус некоторого маршрута идет с интервалом в десять минут. Пассажир в какой-то момент подходит к остановке. Время, в течении которого пассажир ожидает автобус, представляет случайную величину, имеющую равномерное распределение. Определить дифференциальную функцию распределения этой случайной величины, ее математическое ожидание и дисперсию.
7) По данным задачи 6 определить вероятность того, что пассажир подошедший к остановке, будет ждать автобус менее 4 минут.
8) Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка:
а) меньшая 0,04;
б) большая 0,05.
9) Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 сек.
Форма контроля: Проверка решений задач и заданий