Задания для самостоятельной работы
1) Вероятность того, что из двух приобретенных билетов оба окажутся выигрышными рана 0,49. Определить вероятность того, что из шести билетов выиграют три.
2) Вероятность прокола колеса автомобиля при поездке равна 0,1. На сколько вероятнее доехать до конечного пункта следования с запасным колесом, чем без запасного колеса?
3) Игральная кость бросается 120 раз. Определить наивероятнейшее число выпадений шести очков на верхней грани кости.
4) На складе находится продукция двух цехов, причем в продукции плюс первого цеха содержится 60 % изделий высшего сорта, в продукции второго цеха – 70%. Для контроля качества продукции берутся 50 продукций первого цеха и 40 изделий второго цеха. Определить, в продукции какого цеха наивероятнейшее число изделий высшего сорта окажется наибольшим.
5) В зимнее время вероятность своевременного прибытия поезда на станцию принимается равным 0,8. Определить вероятность того, что из 30 ожидаемых поездов 25 прибудут своевременно.
6) На факультете института 40% всех студентов занимаются в спортивных секциях. Найти наивероятнейшее число студентов, занимающихся в спортивных секциях, их 250 студентов и вероятность того, что именно это число студентов занимается в спортивных секциях.
7) Школьники посадили на своем участке 500 деревьев. Вероятность того, что дерево приживется равна 0,6. Определить вероятность того, что число прижившихся деревьев окажется в пределах от 278 до333.
8) Известно, что для присуждения спортивных разрядов по стрельбе необходимо набрать хотя бы 90 очков из 100 возможных. Определить вероятность того, что стрелок станет разрядником, если для него вероятность попадания в цель при каждом выстреле равна 0,8.
9) При массовом выпуске некоторой продукции бывает в среднем 4 % брака. Определить вероятность того, что в партии 625 единиц этой продукции отклонение от установленного процента брака по абсолютной величине будет не более чем 0,02.
10) Вероятность безбилетного проезда на транспорте равна 0,05. Обследовано 400 человек. С вероятностью 0,9545 определить:
а)границы изменения относительной частоты безбилетных пассажиров;
б)границы, в которых заключено число безбилетных пассажиров среди обследованных.
11) Всхожесть семян характеризуется вероятностью 0,7. Определить, сколько нужно посеять семян, чтобы с вероятностью 0,9973 можно было утверждать, что частность проросших семян будет отличатся от 0,7 по абсолютной величине не более, чем на 0,02.
Тема. Случайная величина
1. Дискретная (прерывная) случайная величина
Пример 1.В некотором цехе изделия второго сорта составляют 10% всех изделий. Составить закон распределения числа изделий второго сорта из взятых неудачу трех изделий. Вычислить числовые характеристики случайной величины Х – числа изделий второго сорта.
Решение. Пусть Х – число изделий второго сорта (т.е. число наступления события). Тогда вероятность появления изделия второго сорта в одном отдельно взятом испытании р=0,1,q=1-р=0,9. Наименьшее значение, которое может принимать случайная величина Х равно нулю, т.е. среди трех наудачу взятых изделий нет изделия второго сорта. Далее будут значения х=1, х=2, х=3. А вероятности при составлении закона распределения вычисляются с использованием формулы Бернулли.
;
_____________
Закон распределения случайной величины Х будет иметь вид
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,729 |
0,243 |
0,027 |
0,001 |
Вычислим числовые характеристики случайной величины Х.
Математическое ожидание:
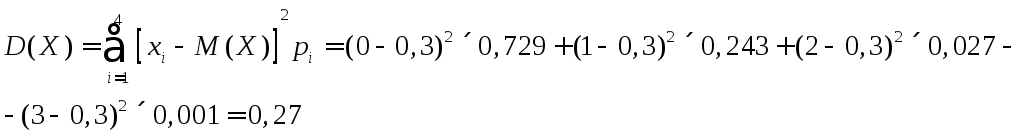
или, используя упрощенную формулу дисперсии, вычислим:
Пример 2. Стрелок стреляет в тире на приз за попадание. Вероятность попадания при каждом выстреле равна 0,3. Разрешается сделать не более четырех выстрелов. Стрелок получает приз после первого же попадания. Составить закон распределения числа выстрелов, в результате которых стрелок может получить приз.
Решение. Пусть Х – число выстрелов
(т.е. число испытаний), в результате
которых стрелок может получить приз.
Случайная величина Х принимает значение
1, 2, 3, 4. Вероятности при составлении
закона распределения будем вычислять
с применением теорем сложения и умножения
вероятностей. Сделав один выстрел,
стрелок сразу же получает приз, если он
попал, следовательно,
.
Если сделал два выстрела, стрелок
получает приз, то это означает, что после
первого выстрела стрелок промахнулся,
а вторым выстрелом он поразил мишень,
следовательно,
и т.д. При четырех выстрелах возможны
две комбинации: стрелок три раза
промахнулся и последний четвертый раз
попал или четыре раза промахнулся:
.
-
X
P
1
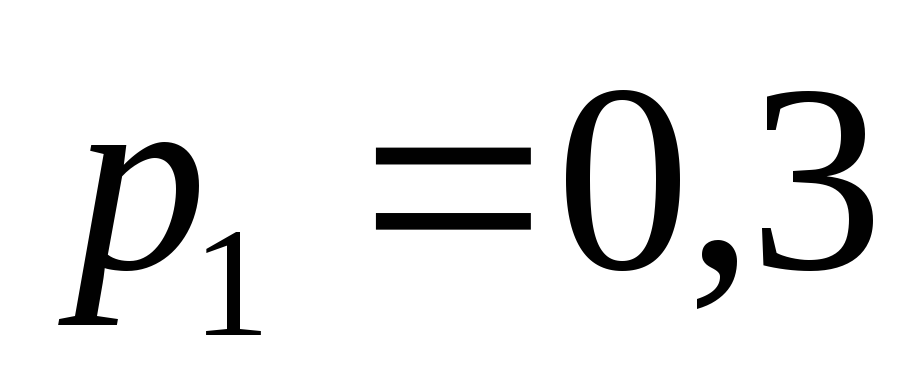
2
3
4
Вычислим числовые характеристики случайной величины:
.