
- •Казанский кооперативный институт (филиал)
- •Математика Задания и методические указания для самостоятельной работы студентов
- •Председатель з.Н. Мирзагалямова
- •Введение
- •Тематический план самостоятельной работы
- •Линейная алгебра
- •Задания для самостоятельной работы
- •Аналитическая геометрия и векторный анализ Аналитическая геометрия Прямая на плоскости
- •Задания для самостоятельной работы
- •Кривые второго порядка
- •Задания для самостоятельной работы
- •Векторный анализ Вектор в декартовой системе координат
- •Задания для самостоятельной работы
- •Скалярное, векторное, смешанное произведение векторов.
- •Задания для самостоятельной работы
- •Функции комплексного пременного
- •Дифференциальное и интегральное исчисления Пределы.
- •Задания для самостоятельной работы
- •Основы дифференциального исчисления
- •Задания для самостоятельной работы
- •Полное исследование функции
- •Задачи для самостоятельной работы
- •Интегральное исчисление Примеры приемов интегрирования
- •Задания для самостоятельной работы
- •Примеры вычисления определенного интеграла
- •Задания для самостоятельной работы
- •Линии уровня.
- •Дифференциальное исчисление функции многих переменных
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •3. Теорема умножения вероятностей для зависимых событий
- •4. Вероятность появления хотя бы одного события из независимых событий
- •5.Формула полной вероятности
- •6. Вероятность гипотез. Формула Байеса
- •Задания для самостоятельной работы
- •Тема. Повторные независимые испытания
- •1. Формула Бернулли
- •2. Локальная теорема Лапласа
- •3. Наивероятнейшее число наступлений события (наивероятнейшая частота)
- •4. Интегральная теорема Лапласа
- •Задания для самостоятельной работы
- •Тема. Случайная величина
- •1. Дискретная (прерывная) случайная величина
- •2. Теоремы о математическом ожидании и дисперсии числа появлений события в n независимых испытаниях
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Тема. Законы распределения случайных величин
- •1. Нормальное распределение
- •2. Равномерное распределение
- •Задания для самостоятельной работы
- •Математическая статистика Тема. Выборочный метод
- •Задания для самостоятельной работы
- •1. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (большие независимые выборки объемов ).
- •3.Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности (сравнение со стандартом а).
- •Задания для самостоятельной работы
- •Гармонический анализ
- •Функциональный анализ
- •Специальные разделы математики Элементы линейного программирования
- •Задачи для контрольной работы
- •Транспортная задача
- •Задачи для контрольной работы
- •Игры с “природой”
- •Задачи для контрольной работы
- •Рекомендуемая литература
- •080401.65 «Товароведение и экспертиза товаров»
- •420045 Республика Татарстан, г. Казань,
Задания для самостоятельной работы
Найти угол между векторами
 и
и ,
если
,
если
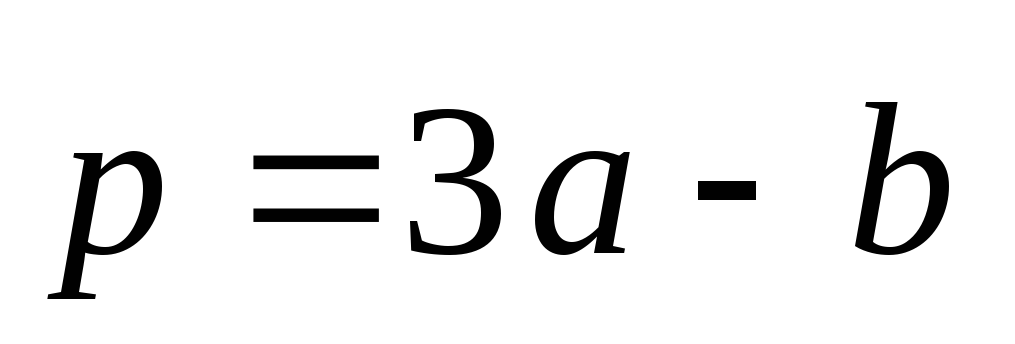 ,
,
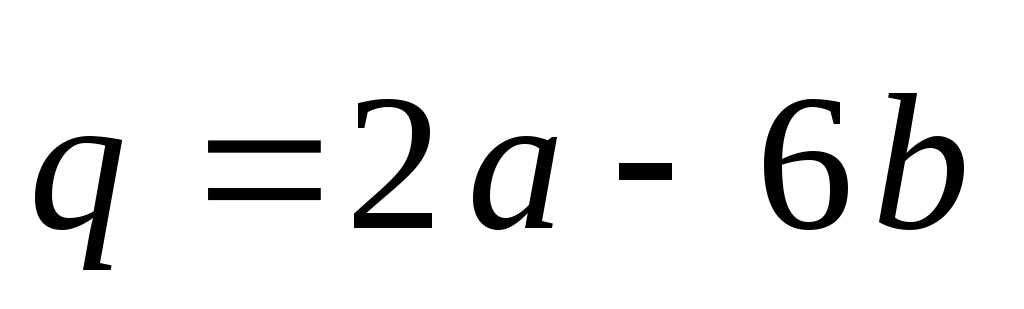 .
.
А)
![]() ,
,![]() ,
,
Б)
![]() ,
,![]() ,
,
В)
![]() ,
,![]() ,
,
2. Параллелограмм построен на векторах
![]() и
и![]() ,
где А)
,
где А)![]() ,
,![]() ,
,![]() .
.
Б)
![]() ,
,![]() ,
,![]() .
.
В)
![]() ,
,![]() ,
,![]() .
.
Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
Компланарны ли векторы
А)
![]() ,
,![]() ,
,![]() ,
,
Б)
![]() ,
,![]() ,
,![]() ,
,
В)
![]() ,
,![]() ,
,![]() ?
?
Найти точку
 ,
делящую отрезок
,
делящую отрезок в отношении
в отношении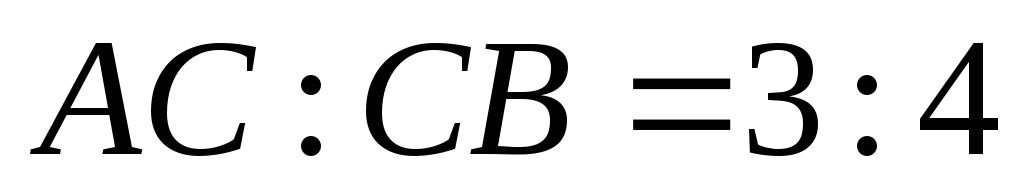 ,
если
,
если
А)
![]() .
.
Б)
![]() .
.
В)
![]() .
.
Пирамида задана координатами своих вершин
А)
![]() ,
,![]() ,
,![]() ,
,
Б)
![]() ,
,![]() ,
,![]() ,
,
В)
![]() ,
,![]() ,
,![]() .
.
Требуется найти: 1) длины ребер
![]() и
и![]() ;
2) угол между ребрами
;
2) угол между ребрами![]() и
и![]() ;
3) площадь грани, содержащей вершины
;
3) площадь грани, содержащей вершины![]() ;
4) объем пирамиды; 5) уравнения прямых
;
4) объем пирамиды; 5) уравнения прямых![]() и
и![]() ;
6) уравнение высоты
;
6) уравнение высоты![]() ,
опущенной из вершины
,
опущенной из вершины![]() на плоскость
на плоскость![]() ;
7) расстояние от вершины
;
7) расстояние от вершины![]() до плоскости
до плоскости![]() ;
8) угол между ребром
;
8) угол между ребром![]() и гранью, содержащей вершины
и гранью, содержащей вершины![]() .
.
Форма контроля: Проверка решений задач и заданий
Функции комплексного пременного







Форма контроля: Проверка решений задач и заданий
Дифференциальное и интегральное исчисления Пределы.
Пример: Найти пределы функций![]()
а)
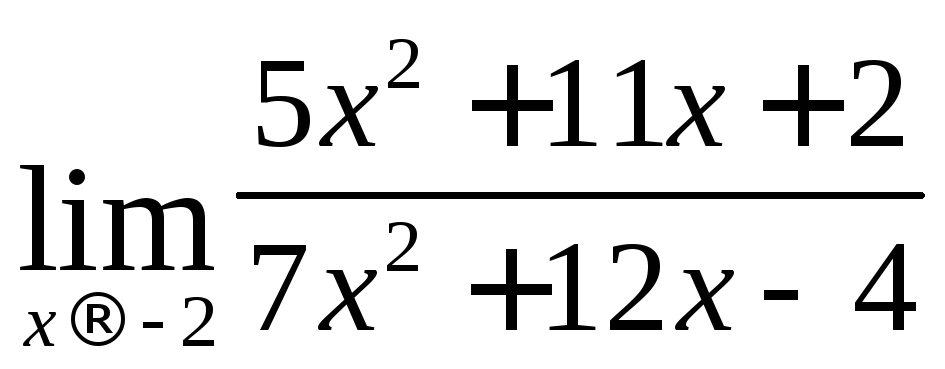 б)
б)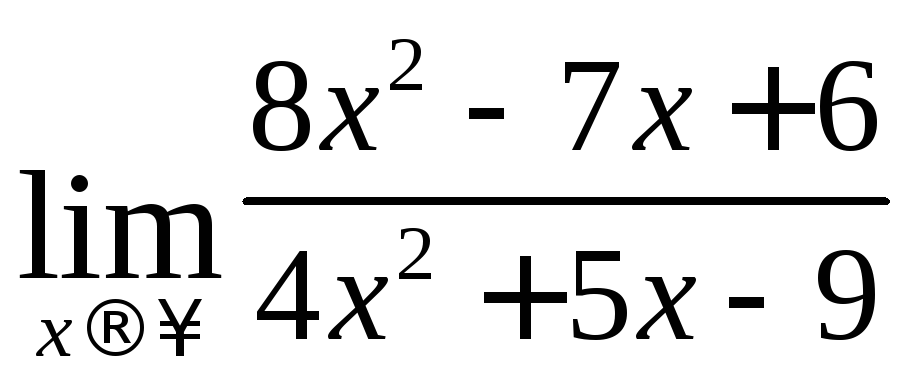
в)
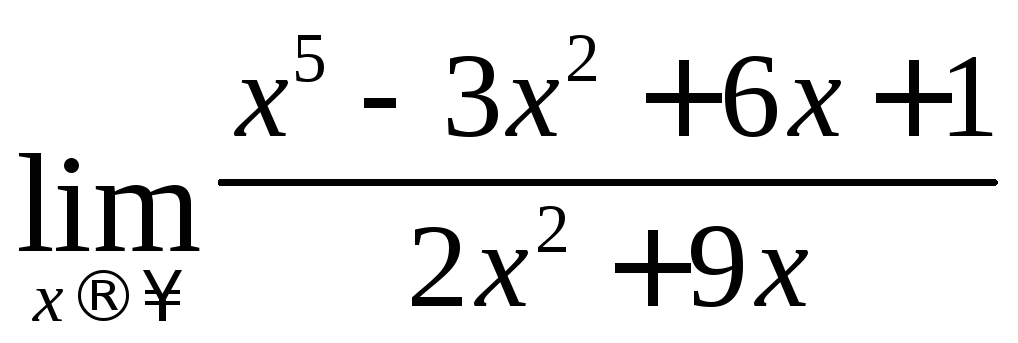 г)
г)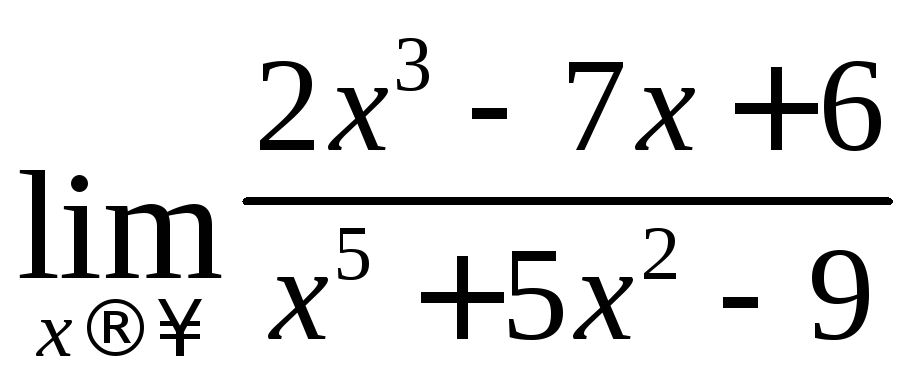
д)
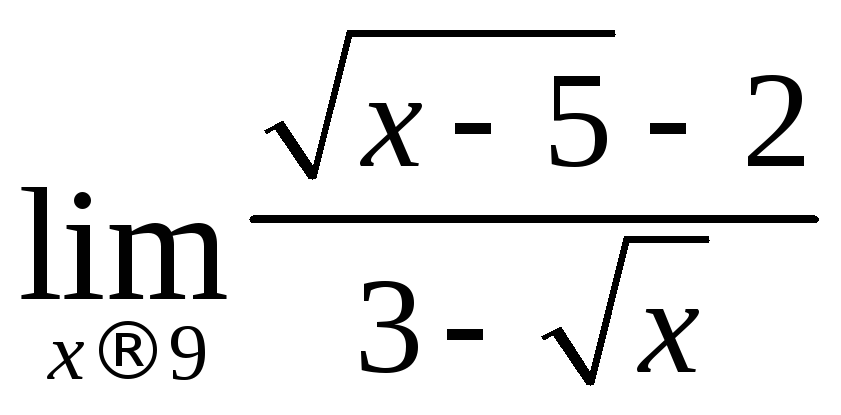 е)
е)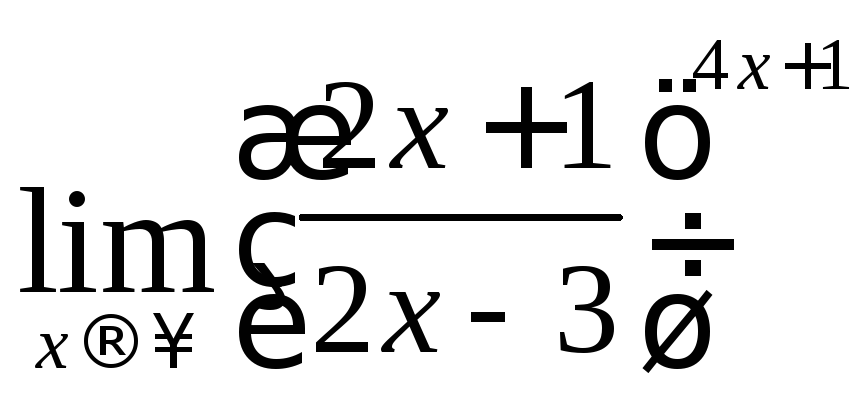
ж)
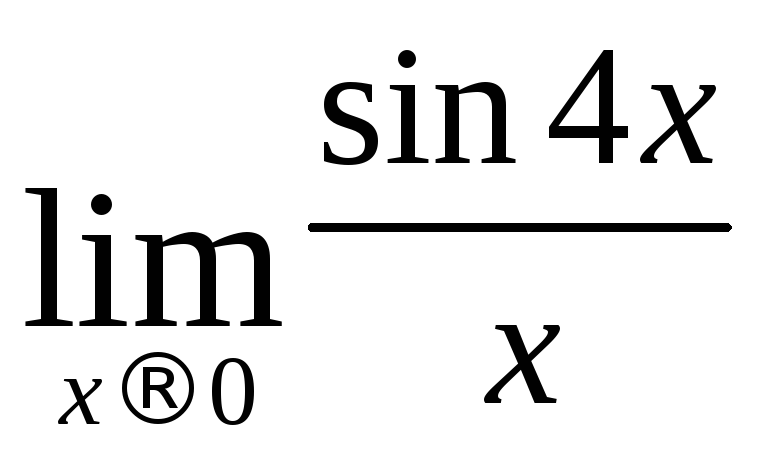 з)
з)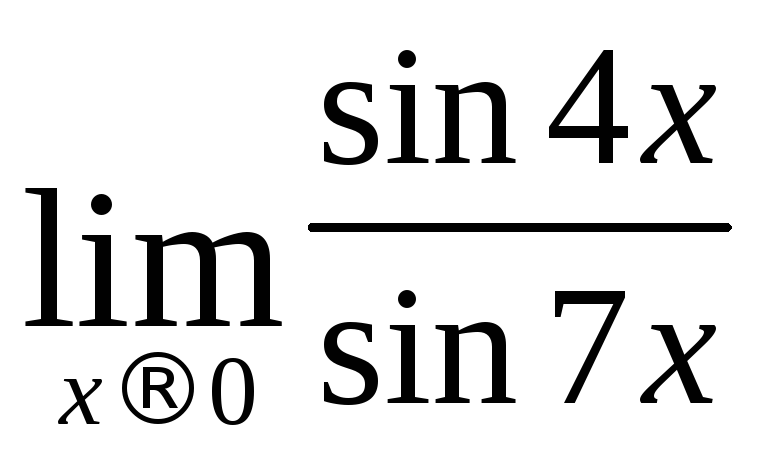
Решение:
а) Непосредственная подстановка
предельного значения аргумента x=2
приводит к неопределённости вида (0/0).
Чтобы раскрыть эту неопределённость,
разложим числитель и знаменатель на
множители по формуле![]() гдеx1иx2находятся как корни квадратных трёхчленов
стоящих в числители и знаменатели
гдеx1иx2находятся как корни квадратных трёхчленов
стоящих в числители и знаменатели
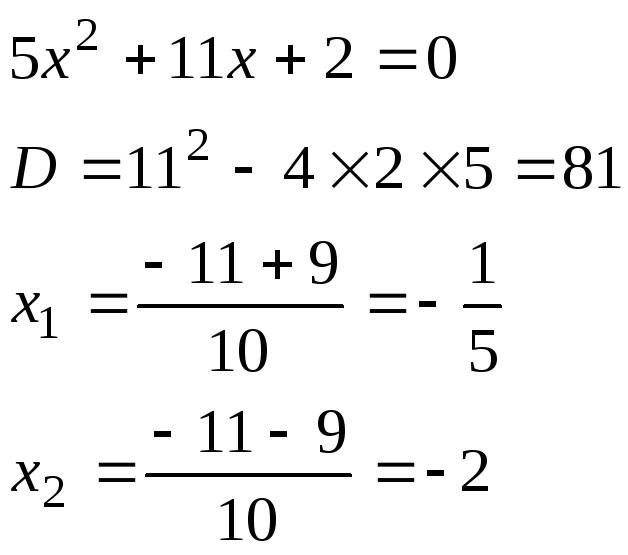
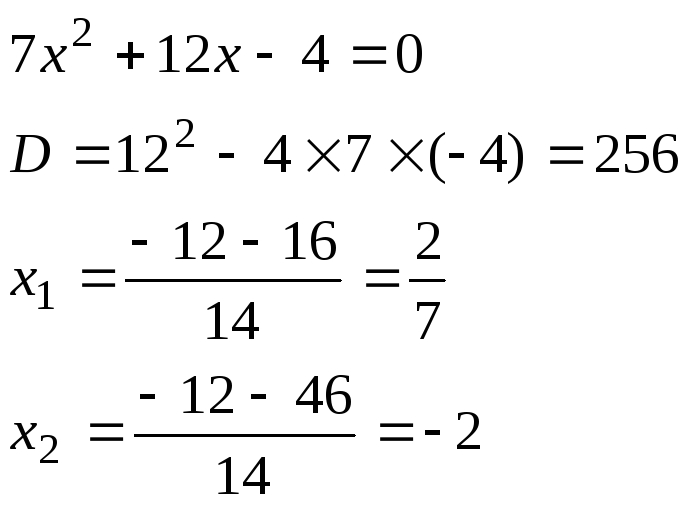
Так как аргумент xтолько стремится к своему предельному значению -2, но не совпадает с ним, то множитель (x+2) отличен от нуля прих→ -2 и можно сократить на (x+2). В результате будем иметь:
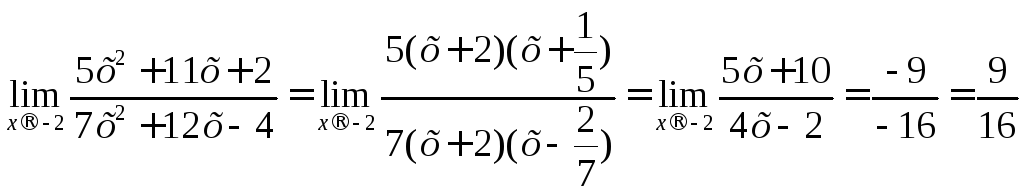
![]()
![]()
б) При xимеем неопределенность вида (/). Разделим числитель и знаменатель дроби наx2 (x0) при х. Получим:
![]()
![]() =
=![]()
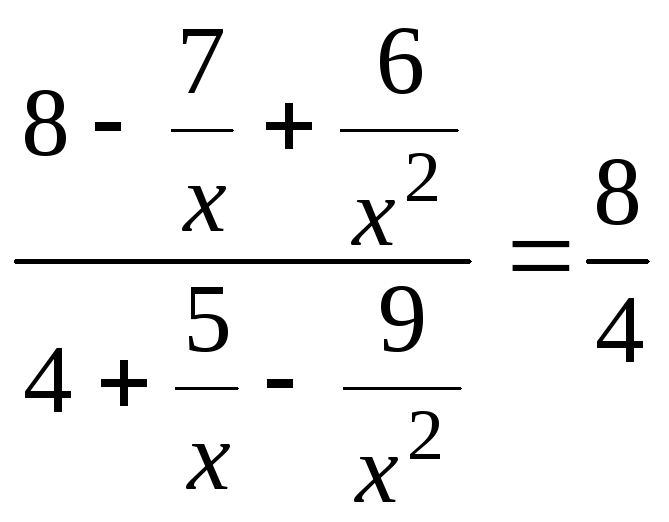 = 2,
= 2,
(так как при х7/x 0, 6/x2 0, 5/x 0, 9/x2 0).
в) Непосредственная подстановка даёт неопределённость вида(0/0).
Используем формулу сокращённого
умножения (a-b)(a+b)=a2
+b2. Умножим
числитель и знаменатель дроби на
выражения:![]() и
и![]() .
.
Имеем:
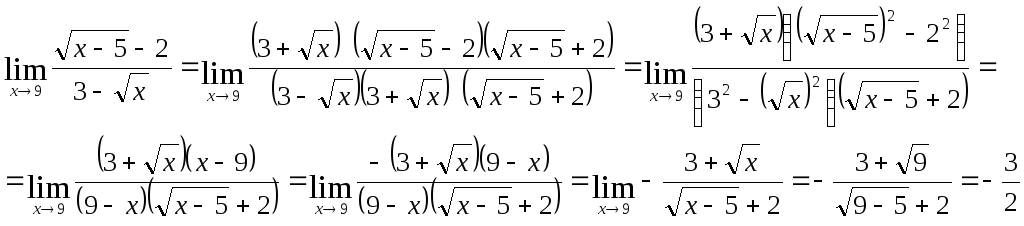
г) При хоснование![]() стремится к 1, а показатель степени
(4x+1) стремится к.
Значит, имеем неопределённость вида
(1).
стремится к 1, а показатель степени
(4x+1) стремится к.
Значит, имеем неопределённость вида
(1).
Будем использовать второй замечательный
предел
![]() .
.
Сведем исходное выражение заданного предела ко второму замечательному пределу:
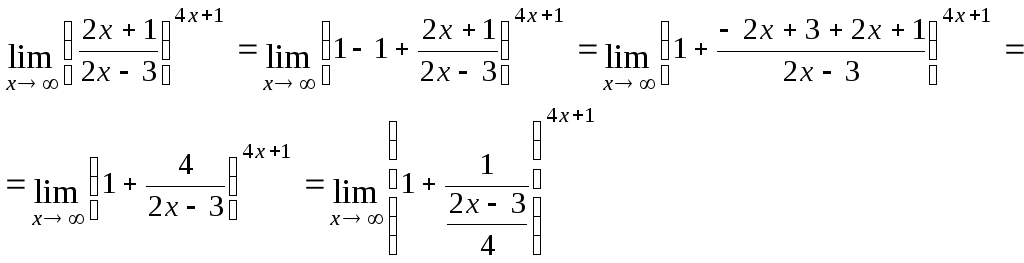
Положим
![]() .
Тогда
.
Тогда![]() .
Выразим показатель степени через
переменную
.
Выразим показатель степени через
переменную![]() :
:![]()
Кроме того, при х, новая переменнаяy.
Таким образом
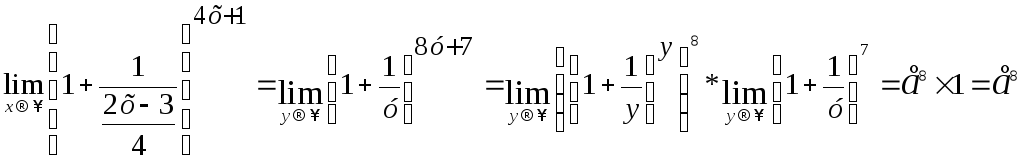
Задания для самостоятельной работы
1) а)
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)![]()
![]()
2) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)![]()
![]()
3) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)![]()
![]()
4) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)![]()
![]()
5) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)
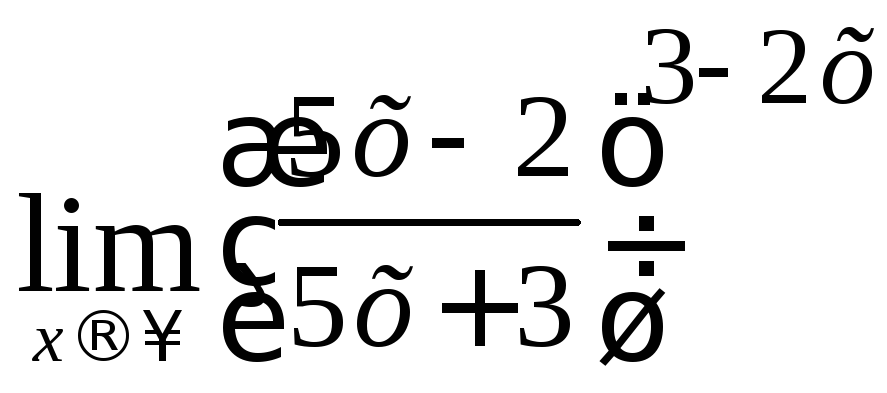
6) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)![]()
![]()
7) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)![]()
![]()
8) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)![]()
![]()
9) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)![]()
![]()
10) а)
![]()
![]() б)
б)![]()
![]() в)
в)![]()
![]() г)
г)
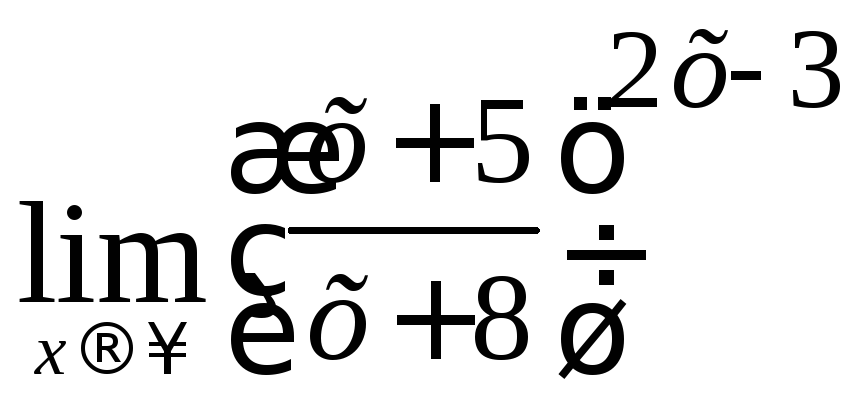
Форма контроля: Проверка решений задач и заданий
Основы дифференциального исчисления
Пример.Найти производные функций:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)y=ln
; г)y=ln![]() ;
д)
;
д)![]() .
.
Решение:
а) Используя правило дифференцирования дроби и таблицы производных элементарных функций, получим:
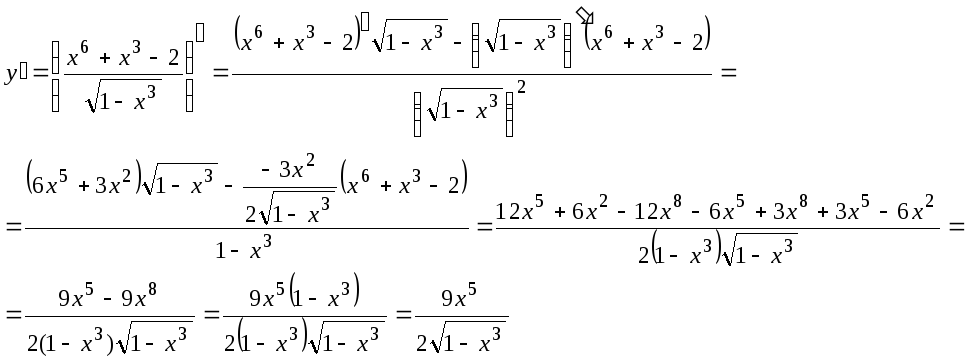 б)
Воспользуемся вначале правилом
дифференцирования сложной степенной
функции:
б)
Воспользуемся вначале правилом
дифференцирования сложной степенной
функции:![]()
Найдём далее производную разности
(3arctg2x–ln(1+4![]() 2))
2))
Производная выражения 3arctg2xесть производная сложной, показательной функции. Она равна:
(3 arctg2x
)/= 3 arctg2x
ln3 (arctg2x)/=3
arctg2x
ln3![]()
Производная выражения
![]() есть производная сложной логарифмической
функции. Она равна (ln(1+4
есть производная сложной логарифмической
функции. Она равна (ln(1+4![]() 2))/
2))/![]()
Окончательно имеем
y/=![]() (3
arctg2x
ln3
(3
arctg2x
ln3![]() )=
)=
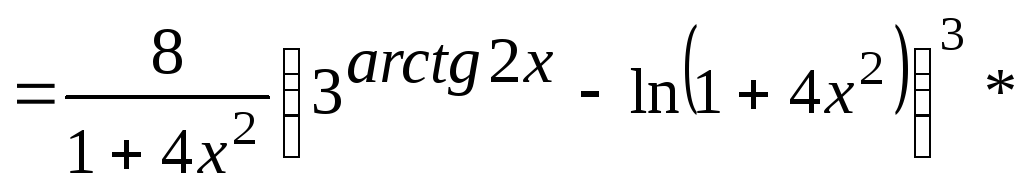 (3 arctg2x
ln3-4x)
(3 arctg2x
ln3-4x)
в) Воспользуемся вначале правилом дифференцирования сложной показательной функции:
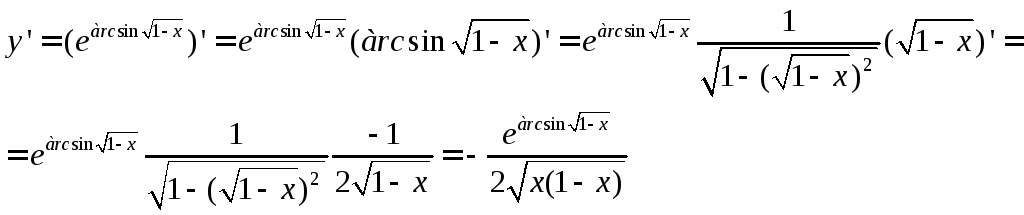
Окончательно будем иметь:
![]() .
.
г) Предварительно преобразуем функцию,
используя свойство логарифмов:
y=ln![]() ln
ln![]() (ln
(ln![]() ln
ln![]() ).
).
Применяя правило дифференцирования разности функций и сложной логарифмической функции, получим:
 (ln
(ln![]() ln
ln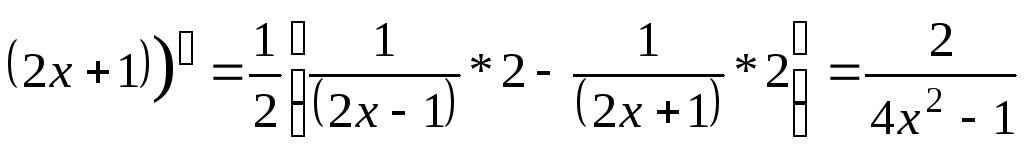 .
.
д) Предварительно прологарифмируем по основанию обе части равенства:
ln ![]() = ln(x+1)arctgx
= arctg x
ln(x+1).
= ln(x+1)arctgx
= arctg x
ln(x+1).
Далее продифференцируем обе части, считая lnyсложной функцией от переменнойx:
![]() (
arctg x)
(
arctg x)![]() ln(x+1)
+ arctg x
(ln(x+1))
ln(x+1)
+ arctg x
(ln(x+1))![]() =
= 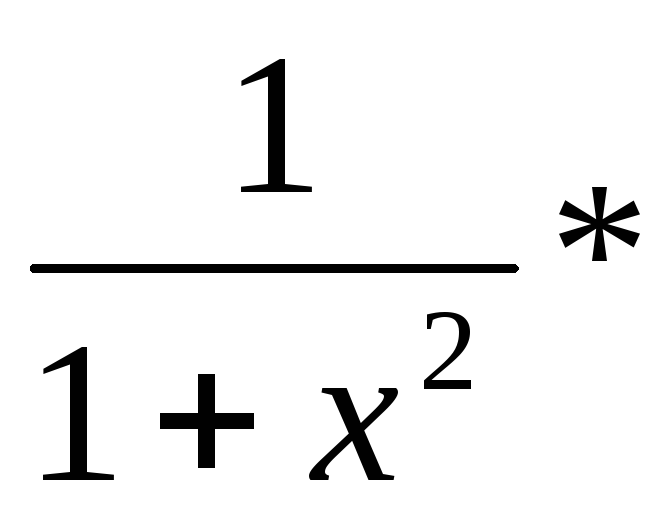 ln(x+1)
+ arctg x
ln(x+1)
+ arctg x
![]()
Окончательно выразим y![]() :
:
![]()
