Векторный анализ Вектор в декартовой системе координат

Пример 1.

Даны векторы . Показать, что векторыиобразуют базис на плоскости и найти координаты векторав этом базисе.

Решение. Если два вектора неколлинеарны (), то они образуют базис на плоскости. Так как, то векторыинеколлинеарны и, значит, образуют базис. Пусть в этом базисе векторимеет координаты, тогда разложение векторапо векторамиимеет вид, или в координатной форме

или

Решив полученную систему уравнений каким-либо образом, получим, что.

Значит . Таким образом, в базисевекторимеет координаты.

Задания для самостоятельной работы

Образуют ли векторы ибазис на плоскости. Если да, то найти координаты векторав этом базисе.

2. .

3. .

4. .

5. .

Скалярное, векторное, смешанное произведение векторов.

Пример 1. Найти угол между векторамии, если,, , .

Решение.Используем формулу. Определим координаты векторови, учитывая, что при сложении векторов мы складываем одноименные координаты, а при умножении вектора на число – умножаем на это число каждую координату этого вектора, а:,.

Найдем скалярное произведение векторов ии их длины.,,. Подставив в формулу, получим. Отсюда.

Пример 2. Параллелограмм построен на векторахи, где,,. Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.

Решение.

,,

.

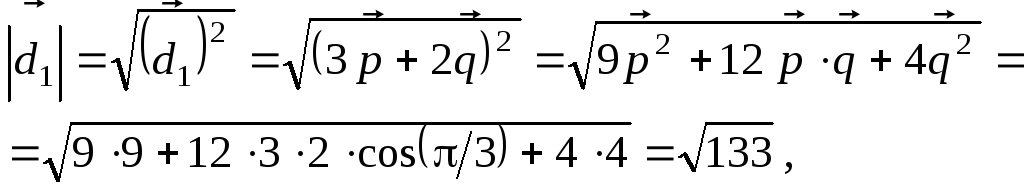
Угол между диагоналями обозначим буквой , тогда

Следовательно, .

Используя свойства векторного произведения, вычислим площадь параллелограмма:

Пример 3.Компланарны ли векторы,,?

Решение.Если векторы компланарны, то по свойству 4) их смешанное произведение равно нулю. Проверим это. Найдем смешанное произведение данных векторов, вычислив определитель:

векторы ,,некомпланарны.

Пример 4.Найти точку, делящую отрезокв отношении, если.

Решение.Определим координаты точки:

. Таким образом,.

Пример 5.Пирамида задана координатами своих вершин,,. Требуется найти: 1) длины ребери; 2) угол между ребрамии; 3) площадь грани, содержащей вершины; 4) объем пирамиды; 5) уравнения прямыхи; 6) уравнение высоты, опущенной из вершинына плоскость; 7) расстояние от вершиныдо плоскости; 8) угол между реброми гранью, содержащей вершины.

Решение.1) Длины ребериопределим как модуль векторовипо формулам;

;

2) Найдем координаты векторов и:

Длины этих векторов, т.е. длины ребери, таковы:,

. Косинус угла между ребрамиивычислим по формуле

;

3) Площадь грани (треугольника) равна половине площади параллелограмма, построенного на векторахи, т.е. половина модуля векторного произведения этих векторов, которое равно

.

Тогда, (кв. ед);

4) Объем пирамиды равен .

(куб. ед);

5) Уравнения прямых инайдем как уравнения прямых, проходящих через две данные точки:

(): ,

(): (абсциссы точекиодинаковые);

6) Направляющим вектором высоты является нормальный вектор плоскости. Получим уравнение плоскости:

,

– уравнение плоскости. Тогда нормальный вектор плоскостиимеет координаты. Канонические уравнения прямой, проходящей через точкупараллельно векторуимеет вид: ;

7) Для вычисления расстояния от вершины до плоскостивоспользуемся формулой. В нашем случае– уравнение плоскостии. Итак,;

8) Угол между прямойи плоскостьюнаходят по формуле:

, где– нормальный вектор плоскости.и (см. п.7).

Таким образом, ,

.