
- •Казанский кооперативный институт (филиал)
- •Математика Задания и методические указания для самостоятельной работы студентов
- •Председатель з.Н. Мирзагалямова
- •Введение
- •Тематический план самостоятельной работы
- •Линейная алгебра
- •Задания для самостоятельной работы
- •Аналитическая геометрия и векторный анализ Аналитическая геометрия Прямая на плоскости
- •Задания для самостоятельной работы
- •Кривые второго порядка
- •Задания для самостоятельной работы
- •Векторный анализ Вектор в декартовой системе координат
- •Задания для самостоятельной работы
- •Скалярное, векторное, смешанное произведение векторов.
- •Задания для самостоятельной работы
- •Функции комплексного пременного
- •Дифференциальное и интегральное исчисления Пределы.
- •Задания для самостоятельной работы
- •Основы дифференциального исчисления
- •Задания для самостоятельной работы
- •Полное исследование функции
- •Задачи для самостоятельной работы
- •Интегральное исчисление Примеры приемов интегрирования
- •Задания для самостоятельной работы
- •Примеры вычисления определенного интеграла
- •Задания для самостоятельной работы
- •Линии уровня.
- •Дифференциальное исчисление функции многих переменных
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •3. Теорема умножения вероятностей для зависимых событий
- •4. Вероятность появления хотя бы одного события из независимых событий
- •5.Формула полной вероятности
- •6. Вероятность гипотез. Формула Байеса
- •Задания для самостоятельной работы
- •Тема. Повторные независимые испытания
- •1. Формула Бернулли
- •2. Локальная теорема Лапласа
- •3. Наивероятнейшее число наступлений события (наивероятнейшая частота)
- •4. Интегральная теорема Лапласа
- •Задания для самостоятельной работы
- •Тема. Случайная величина
- •1. Дискретная (прерывная) случайная величина
- •2. Теоремы о математическом ожидании и дисперсии числа появлений события в n независимых испытаниях
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Тема. Законы распределения случайных величин
- •1. Нормальное распределение
- •2. Равномерное распределение
- •Задания для самостоятельной работы
- •Математическая статистика Тема. Выборочный метод
- •Задания для самостоятельной работы
- •1. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (большие независимые выборки объемов ).
- •3.Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности (сравнение со стандартом а).
- •Задания для самостоятельной работы
- •Гармонический анализ
- •Функциональный анализ
- •Специальные разделы математики Элементы линейного программирования
- •Задачи для контрольной работы
- •Транспортная задача
- •Задачи для контрольной работы
- •Игры с “природой”
- •Задачи для контрольной работы
- •Рекомендуемая литература
- •080401.65 «Товароведение и экспертиза товаров»
- •420045 Республика Татарстан, г. Казань,
2. Теоремы о математическом ожидании и дисперсии числа появлений события в n независимых испытаниях
Пример 3.Вероятность изготовления стандартной лампочки 0,85. Определить математическое ожидание и дисперсию числа стандартных лампочек, если партия ламп состоит из 500 штук.
Решение. Обозначим вероятность появления стандартной электрической лампочки р=0,85, тогдаq=1-р=0,15. Исследованоn= 500 шт.
Найдем М (Х) = np= 500![]() 0,85
= 425;
0,85
= 425;
D
(Х) = npq
=500![]() 0,85
0,85![]() 0,15=63,75
0,15=63,75
Ответ М (Х) = 425; D (x) = 63.75
Примечание: Если при составлении закона распределения Х – число наступлений события (вероятности рассчитывает по формуле Бернулли), то числовые характеристики можно вычислить по формулам:
М(Х)=np,D(Х) =npq
Тогда по данным задачи №1: М(Х) = 3![]() 0,1=0,3;
0,1=0,3;
D(Х)
= 3![]() 0,1
0,1![]() 0,9=0,27
0,9=0,27
Задания для самостоятельной работы
1) Вероятность возникновения погрешности при изменении равна 0,2. Проведено три измерения. Составить закон распределения случайной величины – числа измерений произведенных без погрешности. Вычислить числовые характеристики: математическое ожидание М(Х), дисперсию D(Х).
2) Прибор укомплектовывается тремя однотипными блоками. Контролер проверяет последовательно каждый блок на работоспособность. Как только выявляется неработающий блок, прибор бракуется. Составить закон распределения случайной величины – числа проверяемых блоков приборов, если вероятность появления неисправного блока равна 0,1. Найти числовые характеристики: М(Х), D(X).
3) Четыре покупателя входят в магазин. Для каждого покупателя вероятность сделать покупку равна 0,6. составить закон распределения случайной величины - числа покупателей, сделавших покупку. Найти числовые характеристики случайной величины: М(Х), D(X).
4) На экзамене студенту задаются дополнительные вопросы, но не более трех. Как только студент правильно отвечает на заданный вопрос, экзаменатор прекращает задавать дополнительные вопросы. Вероятность того, что студент правильно ответит на любой заданный вопрос, равна 0,7. Составить закон распределения случайной величины – числа дополнительных вопросов, заданных студенту. Вычислить: М(Х), D(X).
5) Вероятность того, что телевизор не потребует ремонта в течении гарантированного срока равна 0,8. Составить закон распределения случайной величины – числа телевизоров, которые не потребуют гарантированного ремонта, из пяти проданных телевизоров. Найти числовые характеристики М(Х), D(X).
6) Дается пять попыток включить двигатель до первой успешной попытки. Вероятность того, что двигатель включится равна 0,6. Составить закон распределения случайной величины – числа попыток, в результате которых можно запустить двигатель. Найти числовые характеристики: М(Х), D(X).
7) Вероятность того, что из двух, телевизионных камер в данный момент включена одна, равна 0,42. В студии имеются 20 телевизионных камер. Найти вероятность того, что в данный момент включены:
- 18 камер;
- хотя бы 15 камер. (вероятность включения каждой из камер больше 0,5) .
8) Один из видов продукции производится на трех фабриках, входящих в состав производственного объединения. Первая фабрика производит 40% всего выпуска продукции, вторая – 35%, третья – 25%. В продукции первой фабрики обнаружено 30% изделий низкого качества, в продукции второй фабрики - 20%, в продукции третьей фабрики 12%. Какова вероятность того, что среди 500 изделий производственного объединения число изделий высшего качества будет 400 до 410.
9) По данным длительной проверки качества запчастей определенного вида брак составляет 5 %. Изготовлено 500 запчастей. Определить математическое ожидание и дисперсию числа годных запчастей.
10) Всхожесть семян некоторого сорта пшеницы составляет 93%. Определить математическое ожидание и дисперсию числа всходов, если высажено 70 семян.
Пример 1.Случайная величина Х задана интегральной функцией
![]()
 0, при
0, при![]()
F(x)
=![]()
1, при х>1
Определить:
а) дифференциальную функцию f(х),
б) вероятность
![]()
в) числовые характеристики: М(Х), D(Х),![]() .
.
Решение.
а) Найдем f(x).
![]()
 0, при
0, при![]()
f(x)
=![]() =
=![]()
0, при х>1
б) Вычислим
![]()
или
![]()
в) Определим
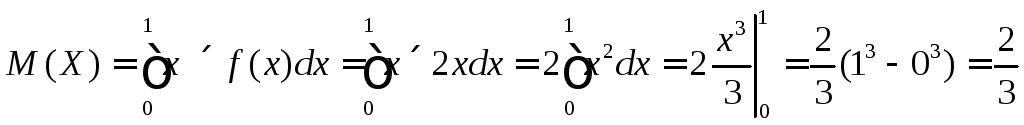

![]()
П ример
2.Случайная величина Х задана
интегральной функцией:
ример
2.Случайная величина Х задана
интегральной функцией:
![]() 0, при
0, при![]()
F(x)=![]()
1, при х>e
Определить:
а) дифференциальную функцию f(х)
б) математическое ожидание и дисперсию этой случайной величины.
Решение.
а )
)
![]() 0, при
0, при![]()
F(x)=![]()
1, при х>e
б) ![]()

