Задания для самостоятельной работы

1. А(-8;-3), В(4; -12), С(8; 10).

2. А(-5; 7), В(7; -2), С(11; 20).

3. А(-12; -1),В (0; -10),С (4; 12).

4. А (-10; 9), В (2; 0),С (6; 22).

5. А (0; 2), В (12; -7), С (16; 15).

6. А(-9; 6), В (3; -3), С (17; 19).

7. А(1; 0), В(13; -9), С(17;16).

8. А (-4; 10), В(8;1), С (12;23).

9. А(2; 5),В(14; -4),С18; 18).

10. А(-1; 4), В(11;-5), С(15;17).

Кривые второго порядка

Пример 1.Найти центр и радиус окружности 2x²+ 2y²+8x - 12y - 6 = 0. Определить количество пересечений с осями координат.

Решение.Приведем исходное уравнение к нормальному виду. Для этого поделим правую и левую части на 2 и сгруппируем переменные

( x² + 4x) + (y² - 6y ) - 3 = 0.

Затем дополним выражения в скобках до полных квадратов

( x² + 4x+ 4 ) - 4 + (y² - 6y+ 9 ) - 9 - 3 = 0.

Свернув выражения в скобках и собрав свободные члены, получим

( x² + 2 )²+ (y² - 3 )²= 16.

Следовательно, центр окружности О(x₀,y₀) находится точке О(-2; 3), радиус равенR =4.

Так как радиус окружности больше расстояний от центра до осей координат, т.е.R>|x₀|,R>|y₀| илиR>|-2|,R>|3|, то окружность «достает» до обеих осей и, следовательно, имеет четыре точки пересечения.

Пример 2.Написать каноническое уравнение эллипса, симметричного относительно осей координат, если расстояние между фокусамиF₁F₂= 6, а эксцентриситет= 3/5.

Решение.Значениес найдем как половину расстояния между фокусами

с = 6/2 = 3.

Т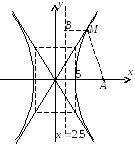ак как эксцентриситет=c/a, имеем

3/5 = 3/a или 3a = 15,a = 5

Далее обе части выражения возведем в квадрат.

В итоге получим c² =a² –b² , откуда 9 = 25 -b² илиb² = 16.

Окончательно запишем .

Пример 3.Составить уравнение геометрического места точек, отношение расстояний которых до данной точки А(10; 0) и до данной прямойх = 2,5 равно числу 2. Полученное уравнение привести к каноническому виду и затем построить кривую.

Решение.Пусть точка М(х,у) лежит на искомой линии, точкаBна прямой. По условию задачи.

Подставим в это соотношение координаты точек. Будем иметь:

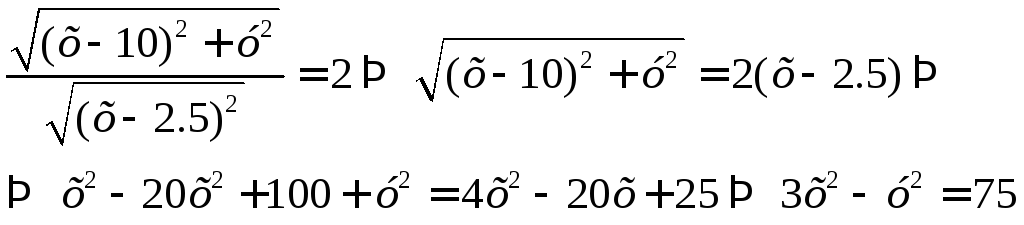
Разделив обе части данного уравнения на 75, приведём его к каноническому виду:

.

Получили уравнение гиперболы, написанное в каноническом виде, где вещественная полуось a = 5, а мнимая полуось

Задания для самостоятельной работы

1. Найти центр и радиус окружности, определить количество пересечений с осями координат и расстояние от центра окружности до данной точки М(х,у), если окружность задана уравнением:

1) x²+ y² - 4x - 8y -11 = 0; M(-3; 2).

2) 2x²+ 2y² + 12x - 8y - 6 = 0; M(0; -2).

3) x²+y² - 10x + 6y - 2 = 0;M(4; - 4).

4) 3x²+ 3y²+ 6x - 72 = 0;M(1; 3).

2. Написать каноническое уравнение эллипса, симметричного относительно осей координат, если известно расстояние между фокусами F₁F₂и эксцентриситет:

1) F₁F₂= 2,= 1/2.

2) F₁F₂= 2,= 1/3.

4. Написать каноническое уравнение эллипса, симметричного относительно осей координат, если известна большая полуось а и эксцентриситет:

1) а =,=.

2) а =,=.

5. Составить уравнения геометрического места точек, отношения расстояний которых до данной точки А(x,y) и до данной прямойx=a равно числуh. Полученное уравнение привести к каноническому виду. Затем построить кривую.

1) A(-8;0),x= -9,h = ;

2) A(-6;0), x = -8, h = ;

3) A(-4;0), x = -1, h = 2;

4) A(-3;0), x = -4/3, h = 1,5;

5) A(-2;0), x = 2,5, h = 1;

6) A(2;0), x = 4,5, h = 2/3;

7) A(3;0), x = 4/3, h = 1,5;

8) A(4;0), x = 5, h = 1;

9) A(6;0), x = 1,5, h = 2.

Форма контроля: Проверка решений задач и заданий