Задачи для самостоятельной работы

Провести полное исследование функции и построить ее график

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

Форма контроля: Проверка решений задач и заданий

Интегральное исчисление Примеры приемов интегрирования

Найти неопределённый интеграл.

а) (^1+sin7x)

Решение

Для вычисления интеграла применим способ подстановки. Пусть 1+sin7=t. Тогдаd(1+sin7)=или 7cos7илиcos7=Подставив полученные выражения в интервал, будем иметь

cos7*5^(1+sin7x) ==+C

Сделаем проверку дифференцированием:

ln5(1+sin7x)^/ +0=

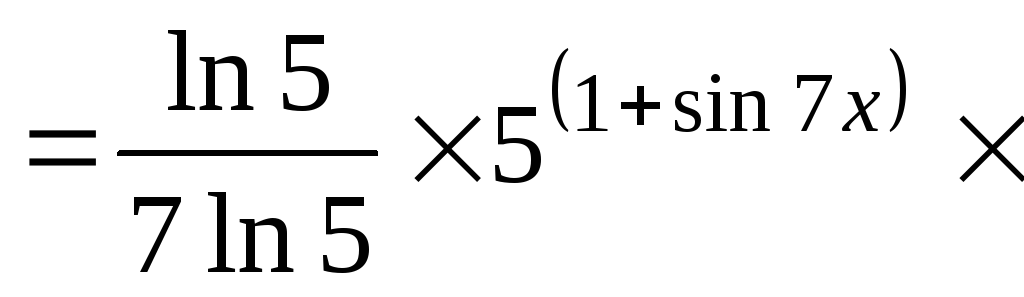7cos7= 5^(1+sin7x)cos7

Получение подинтегральной функции свидетельствует о правильности вычисления интеграла.

б) Найти неопределённый интеграл

Решение

Выделим полный квадрат из квадратного трёхчлена по формуле

В нашем случае:

Получим

Сделав замену: x+1=y;, будем иметь:

arcsin

Возвращаясь к исходной переменной, получим

Сделаем проверку дифференцированием

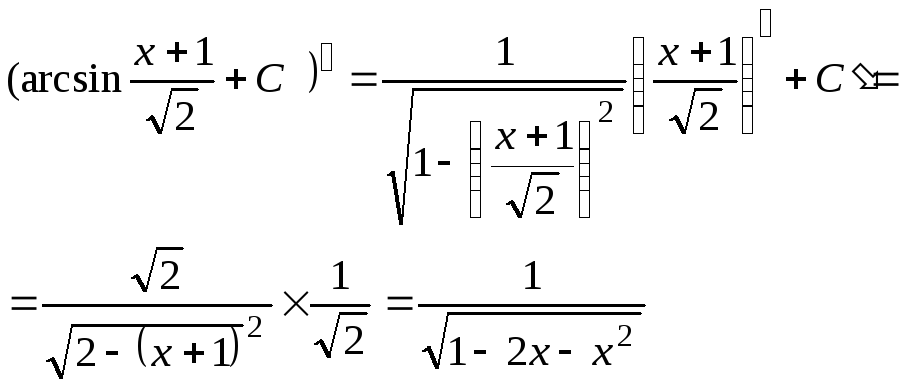
- верно.

в) Найти неопределённый интеграл

Решение

Воспользуемся формулой интегрирования по частям в неопределённом интеграле: udv=u v-vdu

Положим: u=x, dv=sin3. Находимdu=dx,

==

Получим: )=

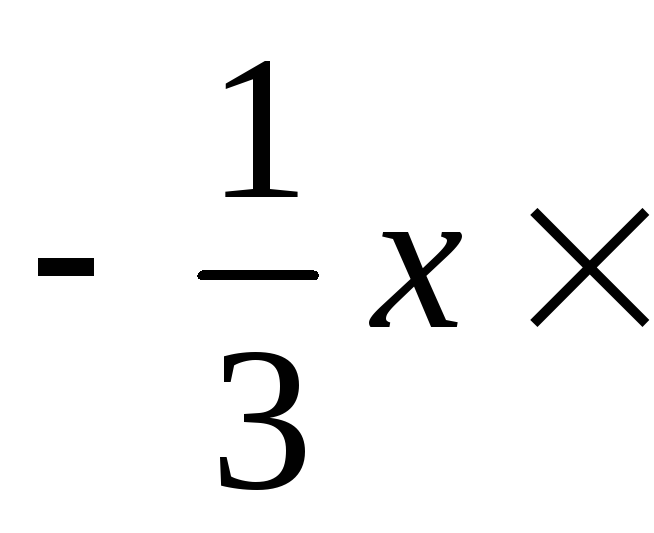
=+= +C

Сделаем проверку дифференцированием:

+((

++

+- верно.

г) Найти неопределённый интеграл

Решение

Подинтегральная функция представляет собой правильную дробь, так как старшая степень числителя меньше старшей степени знаменателя. Найдём корни квадратного трёхчлена

Воспользуемся способом разложения подинтегральной функции на простые дроби

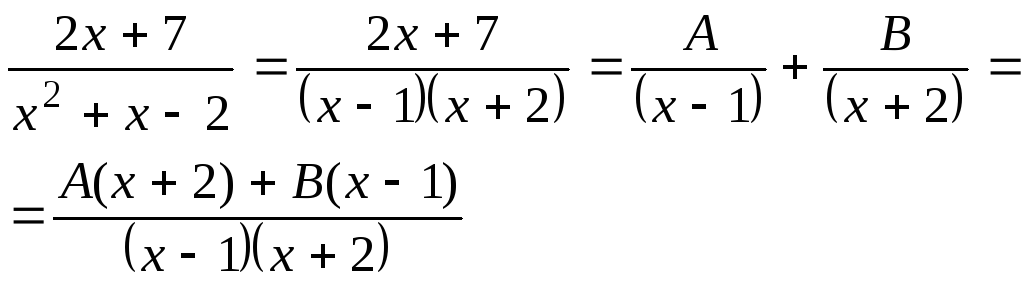
Для нахождения коэффициентов А и Вприменим метод неопределённых коэффициентов.

Способ 1. Для этого приравняем числители, а затем приравняем множители при одинаковых степеняхx.

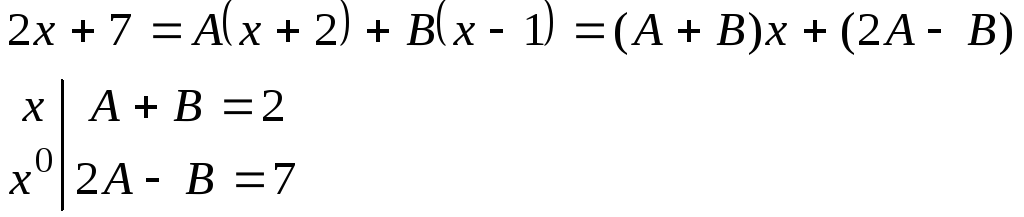
Получим систему двух уравнений с двумя неизвестными

Способ 2.Так как равенство числителей справедливо при любомx, вычислим значения правой и левой частейприх=1 их= - 2. Получим

2+7=А(1+2) +В(1-1) и – 4+7=А(-2+2) +В(- 2-1). Откуда сразу найдемА=3,В= -1.

Далее, определив тем или иным способом коэффициенты, будем иметь

=3ln() -lnln

Сделаем проверку дифференцированием:

(ln(3ln() -ln()+=

-верно.

д) Найти неопределённый интеграл

Разложим подинтегральную функцию на простые дроби

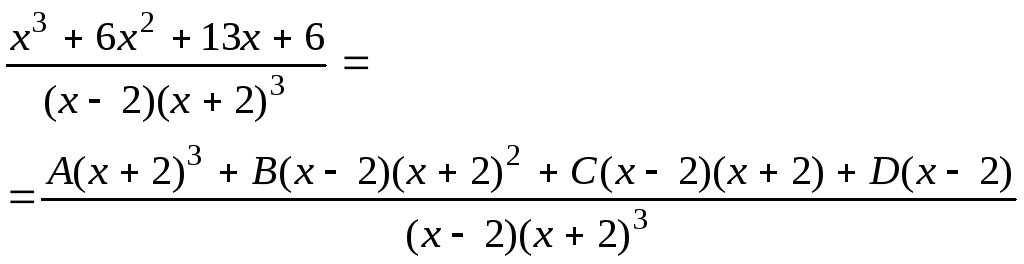
Далее, приравняв числители

( _* )

и раскрыв скобки приравняем коэффициенты при одинаковых степенях х, получим систему из четырех уравнений с четырьмя неизвестными:

A + B = 1, - при х³;

6A + 4B + C = 6, - при х²;

12A – 2B + D = 13, - при х;

8A – 4B – 4C – 2D = 6, - при х⁰.

Прежде чем решать систему воспользуемся вторым способом, положив в ( _* ) х = 2, вычислим значения левой и правой частей:

2³ + 6 _* 2² +13 _* 2 + 6 = А(2 + 2)³ , откуда найдем А = 1.

Положив х = - 2, вычислим (-2)³ + 6 _* (-2)² +13 _*(- 2) + 6 = D(- 2 - 2), откуда D = 1.

Далее, подставив в первое уравнения системы A = 1, получим B = 0;

Подставив известные значения А, В и D в последнее уравнение найдем С: 8 – 0 – 4С – 2 = 6 или С = 0.

Искомый интеграл примет вид

Последние два интеграла находятся легко:

Задания для самостоятельной работы

Найти неопределенные интегралы методом замены переменной:

Найти неопределенные интегралы методом интегрирования по частям: