
- •Казанский кооперативный институт (филиал)
- •Математика Задания и методические указания для самостоятельной работы студентов
- •Председатель з.Н. Мирзагалямова
- •Введение
- •Тематический план самостоятельной работы
- •Линейная алгебра
- •Задания для самостоятельной работы
- •Аналитическая геометрия и векторный анализ Аналитическая геометрия Прямая на плоскости
- •Задания для самостоятельной работы
- •Кривые второго порядка
- •Задания для самостоятельной работы
- •Векторный анализ Вектор в декартовой системе координат
- •Задания для самостоятельной работы
- •Скалярное, векторное, смешанное произведение векторов.
- •Задания для самостоятельной работы
- •Функции комплексного пременного
- •Дифференциальное и интегральное исчисления Пределы.
- •Задания для самостоятельной работы
- •Основы дифференциального исчисления
- •Задания для самостоятельной работы
- •Полное исследование функции
- •Задачи для самостоятельной работы
- •Интегральное исчисление Примеры приемов интегрирования
- •Задания для самостоятельной работы
- •Примеры вычисления определенного интеграла
- •Задания для самостоятельной работы
- •Линии уровня.
- •Дифференциальное исчисление функции многих переменных
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •3. Теорема умножения вероятностей для зависимых событий
- •4. Вероятность появления хотя бы одного события из независимых событий
- •5.Формула полной вероятности
- •6. Вероятность гипотез. Формула Байеса
- •Задания для самостоятельной работы
- •Тема. Повторные независимые испытания
- •1. Формула Бернулли
- •2. Локальная теорема Лапласа
- •3. Наивероятнейшее число наступлений события (наивероятнейшая частота)
- •4. Интегральная теорема Лапласа
- •Задания для самостоятельной работы
- •Тема. Случайная величина
- •1. Дискретная (прерывная) случайная величина
- •2. Теоремы о математическом ожидании и дисперсии числа появлений события в n независимых испытаниях
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Тема. Законы распределения случайных величин
- •1. Нормальное распределение
- •2. Равномерное распределение
- •Задания для самостоятельной работы
- •Математическая статистика Тема. Выборочный метод
- •Задания для самостоятельной работы
- •1. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (большие независимые выборки объемов ).
- •3.Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности (сравнение со стандартом а).
- •Задания для самостоятельной работы
- •Гармонический анализ
- •Функциональный анализ
- •Специальные разделы математики Элементы линейного программирования
- •Задачи для контрольной работы
- •Транспортная задача
- •Задачи для контрольной работы
- •Игры с “природой”
- •Задачи для контрольной работы
- •Рекомендуемая литература
- •080401.65 «Товароведение и экспертиза товаров»
- •420045 Республика Татарстан, г. Казань,
Тематический план самостоятельной работы
|
№ п/п |
Наименование раздела |
Самостоятельная работа студентов, час | ||
|
080401.65 | ||||
|
Очная форма обучения |
Заочная форма обучения с полным сроком |
Заочная форма обучения на базе спо | ||
|
1 |
Линейная алгебра |
28 |
42 |
44 |
|
2 |
Аналитическая геометрия. |
26 |
38 |
40 |
|
3 |
Функции комплексного переменного |
20 |
28 |
30 |
|
4 |
Дифференциальное и интегральное исчисление |
82 |
98 |
100 |
|
5 |
Дифференциальные уравнения |
28 |
44 |
46 |
|
6 |
Последовательности и ряды |
16 |
28 |
30 |
|
7 |
Теория вероятностей |
36 |
54 |
56 |
|
8 |
Математическая статистика |
36 |
54 |
56 |
|
9 |
Векторный анализ и элементы теории поля |
26 |
40 |
42 |
|
10 |
Гармонический анализ |
28 |
38 |
40 |
|
11 |
Численные методы |
34 |
46 |
48 |
|
12 |
Элементы функционального анализа |
32 |
42 |
44 |
|
|
Специальные разделы математики |
- |
- |
- |
|
|
Итого |
392 |
552 |
576 |
Линейная алгебра
Решить систему уравнений двумя способами.
а )
методом Крамера, б) методом обратной
матрицы
)
методом Крамера, б) методом обратной
матрицы![]()
Решение:
а )
Находим основной определитель системы:
)
Находим основной определитель системы:
Так как определитель
![]() не равен нулю, то система имеет единственное
решение. Находим вспомогательные
определители. Определитель
не равен нулю, то система имеет единственное
решение. Находим вспомогательные
определители. Определитель![]() находится из основного определителя
находится из основного определителя![]() путём замены в нём первого столбца на
столбец свободных членов.
путём замены в нём первого столбца на
столбец свободных членов.

О пределитель
пределитель![]() получается из основного определителяпутём замены в нём
второго столбца на столбец свободных
членов.
получается из основного определителяпутём замены в нём
второго столбца на столбец свободных
членов.
Определитель
![]() получается из основного определителяпутём замены в нём
третьего столбца на столбец свободных
членов.
получается из основного определителяпутём замены в нём
третьего столбца на столбец свободных
членов.
По формуле Крамера:


Проверка:

б) Для решения системы уравнения методом обратной матрицы находим определитель системы

Определитель
![]() не равен нулю. Следовательно, обратная
матрица существует.
не равен нулю. Следовательно, обратная
матрица существует.
Находим алгебраические дополнения:
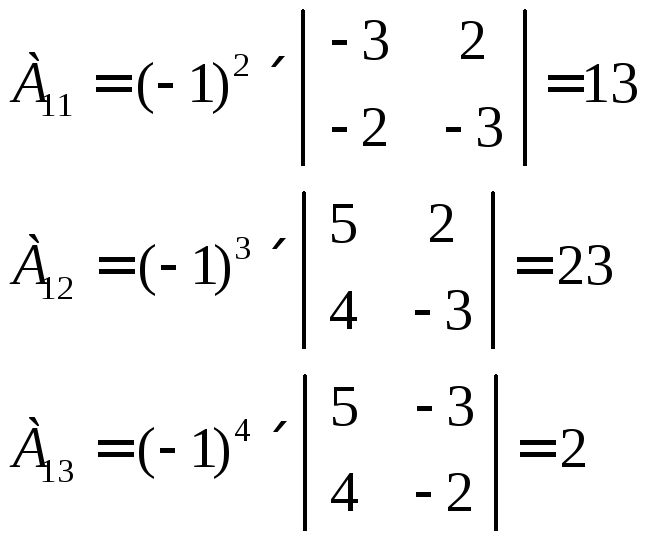


Составим присоединённую матрицу из алгебраических дополнений путём транспонирования строк и столбцов

Разделив каждый элемент присоединённой
матрицы на определитель
![]() ,
получим обратную матрицу:
,
получим обратную матрицу:

Умножив слева обратную матрицу на матрицу - столбец свободных членов, получим искомую матрицу – столбец неизвестных задачи.

Значит: x1 = 1,x2 = 3,x3 = 0.
Задания для самостоятельной работы
Решить систему уравнений:
а) пользуясь методом Крамера
б) методом обратной матрицы
1)
 2)
2)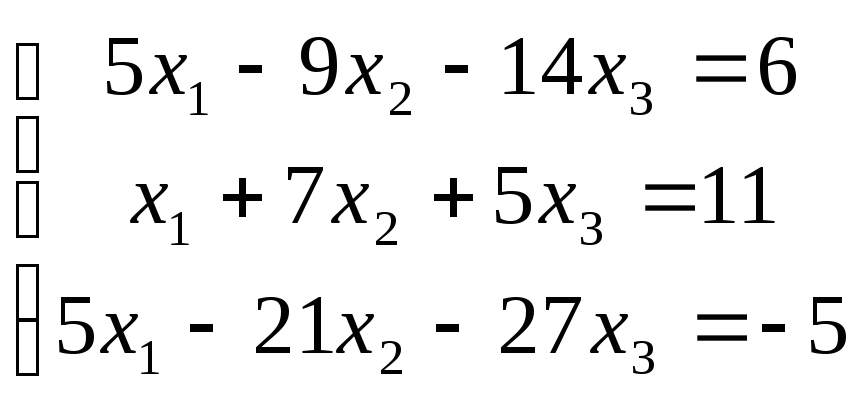
3)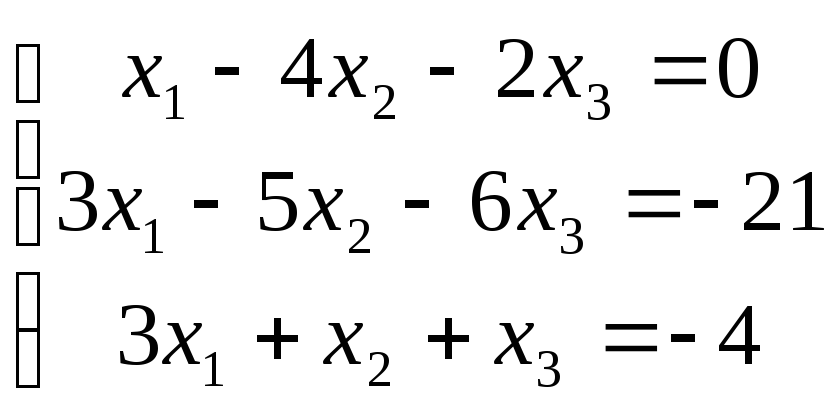 4)
4)
5) 6)
6)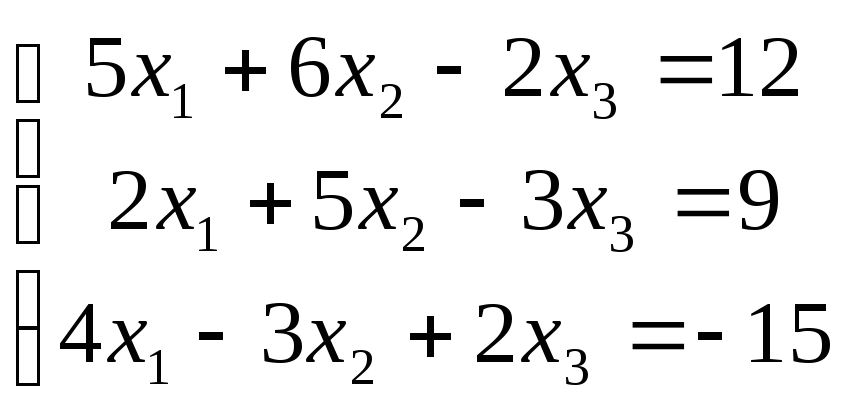
7) 8)
8)
9) 10)
10)
![]()
Форма контроля: Проверка решений задач и заданий
Аналитическая геометрия и векторный анализ Аналитическая геометрия Прямая на плоскости
Пример:Даны координаты вершин треугольника АВС: А (-2;7), В(10;-2), С(8;12).
 Найти:
Найти:
1) Длину стороны АВ.
2) Внутренний угол А.
3) Уравнение медианы СМ.
4) Уравнение высоты СК
5) Точку Fпересечения высотCKиBN.
6) Площадь треугольника Решение
По координатам точек А, В, С построим
треугольник на плоскости XOY.
1)Что бы найти длину стороны АВ
воспользуемся формулой:
![]()
2) Для нахождения внутреннего угла А напишем уравнения сторон АВ и АС. Воспользуемся формулой уравнения прямой, проходящей через две заданные точки.
![]()
АВ:![]() ,
,![]()
АС:![]()
![]()
Угол между прямыми находим по формуле:
tg
![]() arctg2
arctg2
3) Для нахождения уравнения медианы СМ, определим координаты точки М, как середины отрезка АВ:

Уравнение медианы:
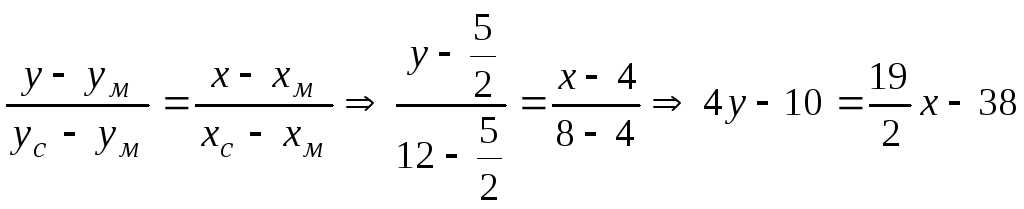 .
.
Окончательно получим
![]() .
.
4) Для нахождения уравнения высоты СК
воспользуемся формулой уравнения
прямой, проходящей через заданную точку
в заданном направлении:
![]() ,
где
,
где (из условия перпендикулярности прямых).
(из условия перпендикулярности прямых).
![]()
5) Для нахождения координат точки
пересечения высот (т.F)
напишем уравнение высотыBN:![]() ,
где
,
где .
.
Тогда
![]() ,
следовательно
,
следовательно![]() - уравнениеBN.
- уравнениеBN.
Далее решим систему уравнений

- уравнение высоты СК
- уравнение высоты BN
![]() xF
= 5yF
= 8 т.е.F(5,8).
xF
= 5yF
= 8 т.е.F(5,8).
6) Чтобы вычислить площадь треугольника предварительно найдем длину высоты СК как расстояние от точки С до прямой АВ по формуле:

Площадь треугольника АВС вычислим по формуле
S![]() (кв.ед)
(кв.ед)
