
- •Министерство образования и науки украины
- •Содержание
- •Глава 1 Арифметико-логические основы эвм
- •1.1 Информационные процессы
- •1.2. Обмен информацией между различными информационными устройствами
- •1.3. Аппаратные средства хранения и обработки информации
- •Глава 2 представление числовой информации в цифровом автомате
- •2.1. Системы счисления и понятие кода
- •2.2. Выбор системы счисления
- •2.3. Формальные правила двоичной арифметики
- •2.4. Перевод числа из одной позиционной системы счисления в другую
- •Глава 3 формы представления чисел в цифровых автоматах
- •3.1. Форма представления двоичных чисел с фиксированной запятой
- •3.2. Представление отрицательных чисел в формате с фиксированной запятой
- •3.3. Форма представление чисел с плавающей запятой
- •3.4. Перевод чисел из формата с фиксированной запятой в формат с плавающей запятой и обратно
- •3.5. Погрешности представления чисел
- •20 [A]ф2n- 1 для целых чисел
- •Глава 4. Арифметические действия с двоичными числами
- •4.1. Сложение двоичных чисел
- •4.1.1. Алгебраическое сложение чисел, представленных в форме с фиксированной запятой
- •4.1.2. Переполнение разрядной сетки
- •4.1.3. Модифицированный прямой, обратный и дополнительный код
- •4.1.4. Алгебраическое сложение чисел, представленных в форме с плавающей запятой
- •4.2. Умножение двоичных чисел
- •4.2.1. Методы умножения двоичных чисел
- •4.2.2. Умножение чисел, представленных в форме с фиксированной запятой
- •4.2.3. Умножение чисел, представленных в форме с плавающей запятой
- •4.2.4. Ускорение операции умножения
- •4.3. Деление двоичных чисел
- •4.3.1. Деление двоичных чисел, представленных в форме с фиксированной запятой.
- •4.3.2. Деление двоичных чисел, представленных в форме с плавающей запятой.
- •4.4. Оценка точности выполнения арифметических операций
- •4.4.1. Погрешность округления
- •Глава 5. Выполнение операций над двоично-десятичными числами
- •5.1. Представление десятичных чисел в д-кодах
- •5.2. Формальные правила поразрядного сложения в д-кодах
- •5.3. Представление отрицательных чисел в д-кодах
- •5.4. Выполнение операций сложения и вычитания в д-кодах
- •5.5. Умножение чисел в д-кодах
- •5.6. Деление чисел в д-кодах
- •5.7. Перевод чисел из д-кода в двоичный и из двоичного в д-код
- •Глава 6 Информационные основы цифровых автоматов
- •6.1. Понятие об информации и её преобразованиях
- •6.2. Преобразования алфавитной информации
- •6.3 Понятие об алгоритме
- •6.4 Понятие о дискретном (цифровом) автомате
- •Глава 7 Основы логического проектирования ца. Основные понятия алгебры логики.
- •7.1. Свойства элементарных функций алгебры логики
- •7.2. Аналитическое представление функций алгебры логики
- •7.3. Совершенные нормальные формы
- •7.4. Системы функций алгебры логики
- •7.5. Числовое и геометрическое представление фал
- •Глава 8 Минимизация функций алгебры логики
- •8.1 Метод Квайна
- •Ядро: мднф:
- •8.2 Метод Квайна-Мак-Класки
- •Простые импликанты: *111, 111*, 0**1
- •8.3 Метод Нельсона
- •8.4 Метод диаграмм Вейча
- •8.5 Метод самопонижающихся циклов
- •8.6 Минимизация монотонных функций
- •8.7 Минимизация конъюнктивных нормальных форм
- •8.8 Минимизация частично определенных булевых функций
- •8.9 Минимизация функций в базисах и-не и или-не
- •8.10 Минимизация систем булевых функций
- •Глава 9 Абстрактная теория автоматов
- •9.2 Декомпозиция абстрактных автоматов
- •Глава 10 Структурная теория автоматов
- •10.1 Композиция автоматов
- •Глава 11 Проектирование асинхронных цифровых автоматов
- •11.1 Проектирование комбинационных схем (кс) с учетом кобъед по входу и по выходу
- •11.2 Проектирование кс на дешифраторах и мультиплексорах
- •11.3 Проектирование кс на пзу
- •11.4 Проектирование кс на плм
- •Глава 12 Канонический метод структурного синтеза ца с памятью
- •12.1 Кодирование
- •12.2 Выбор элементов памяти автомата
- •12.3 Выбор структурно-полной системы элементов
- •12.4 Построение уравнений булевых функций возбуждения и выходов автомата
- •12.5 Построение функциональной схемы автомата
- •Глава 13 Обеспечение устойчивости функционирования ца
- •13.2 Проблема синтеза надёжных схем из ненадёжных элементов
- •13.3 Коды Хэмминга
- •Глава 14 Микропрограммные автоматы
- •14.2 Граф-схемы алгоритмов
11.4 Проектирование кс на плм
Под ПЛМ понимают конструктивный элемент
двухступенчатой структуры, изготавливаемый
в виде программируемой БИС. Настройка
(программирование) ПЛМ осуществляется
пользователем с помощью специального
оборудования (программатора) и заключается
в устранении некоторых связей посредством
фотошаблонов или выжиганием диодных
перемычек. Такая ПЛМ называется (![]() ,
,![]() ,
,![]() )
- ПЛМ, гдеn- число входов ПЛМ;p -
число выходов ПЛМ,k - число конъюнкций,
реализуемых ПЛМ. Входы и выходы ПЛМ
называются столбцами, а конъюнкции
строками. Рассматриваемая ПЛМ содержит
(
)
- ПЛМ, гдеn- число входов ПЛМ;p -
число выходов ПЛМ,k - число конъюнкций,
реализуемых ПЛМ. Входы и выходы ПЛМ
называются столбцами, а конъюнкции
строками. Рассматриваемая ПЛМ содержит
(![]() )
столбцов иkстрок. Число
)
столбцов иkстрок. Число![]() называется площадью ПЛМ.
называется площадью ПЛМ.

П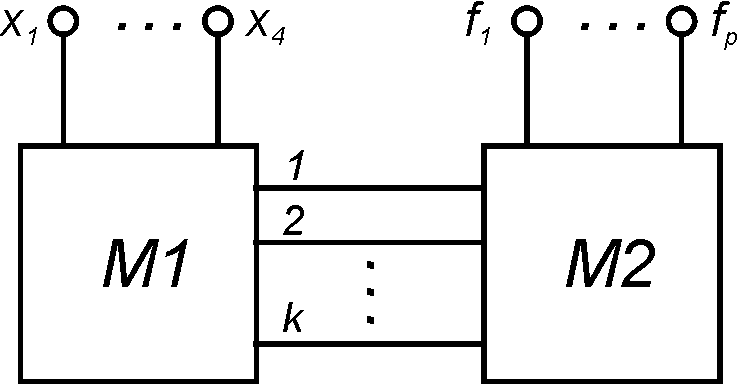 ЛМ
можно представить в виде двух матриц.
Матрица М1 (матрица И) реализуетk
возможных конъюнкций отn-
переменных, матрица М2 (матрица ИЛИ)
реализует возможных дизъюнкций отk- переменных (не более чем отk).
ЛМ
можно представить в виде двух матриц.
Матрица М1 (матрица И) реализуетk
возможных конъюнкций отn-
переменных, матрица М2 (матрица ИЛИ)
реализует возможных дизъюнкций отk- переменных (не более чем отk).
Пусть необходимо реализовать систему функций
![]() ;
;
![]() .
.
Электрическая принципиальная схема описывается уравнениями:
![]() ;
;
![]() .
.
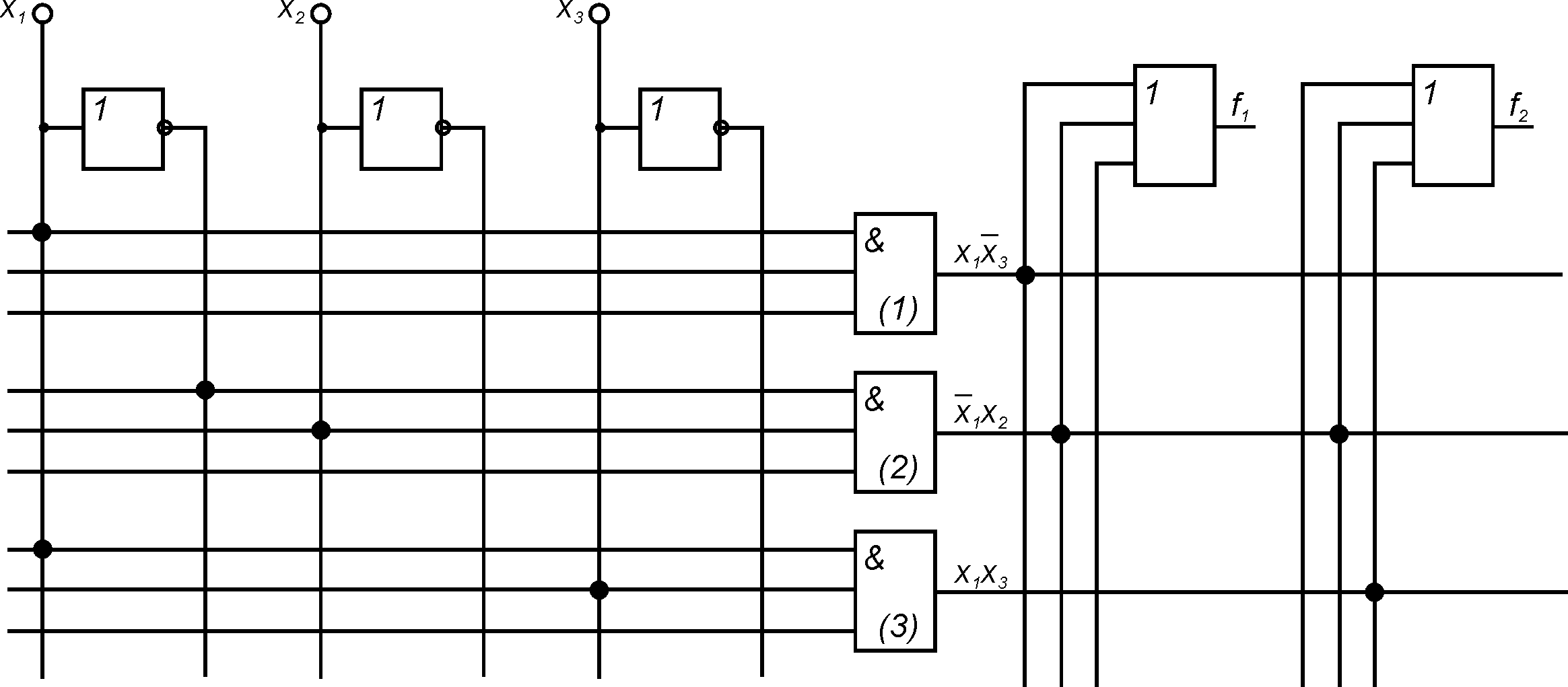
Функциональная схема реализации системы функций

Электрическая схема реализации системы функций
Различают две задачи синтеза КС на ПЛМ:
заданна система булевых функций. Надо реализовать её на ПЛМ, минимизируя суммарную площадь ПЛМ. Задача решается на БИС, структуру которых определяет заказчик;
реализация КС, соответствующей системе булевых функций на минимальном числе ПЛМ с заданными параметрами (
 ,
, ,
, ).
).
Глава 12 Канонический метод структурного синтеза ца с памятью
Канонический метод структурного синтеза ЦА с памятью позволяет свести задачу структурного синтеза произвольного ЦА с памятью к задаче синтеза комбинационных схем. Этот метод оперирует с элементарными автоматами двух классов: элементарными автоматами с памятью (элементы памяти) и элементарными комбинационными автоматами (логические элементы).
Результатом работы метода являются уравнения булевых функций автомата в канонической форме представления. Исходными данными для начала работы служит абстрактный автомат ЦА с памятью. Канонический метод можно условно разделить на следующие этапы:
кодирование;
выбор элементов памяти автомата;
выбор структурно-полной системы элементов;
построение уравнений булевых функций выходов и возбуждения ЦА;
построение функциональной схемы ЦА.
12.1 Кодирование
Абстрактный ЦА может быть описан в виде
![]() .
.
При переходе на структурный уровень
представления каждая буква
![]() входного алфавита
входного алфавита![]() автомата, представляется как двоичный
набор (вектор), число компонентов которого
равно числу физически реализованных
элементарных входных каналов структурного
автомата, т.е. каждая буква
автомата, представляется как двоичный
набор (вектор), число компонентов которого
равно числу физически реализованных
элементарных входных каналов структурного
автомата, т.е. каждая буква![]() кодируется двоичным вектором. Минимальное
число физически реализованных элементарных
входных каналов
кодируется двоичным вектором. Минимальное
число физически реализованных элементарных
входных каналов![]() в автомате может быть определено по
формуле
в автомате может быть определено по
формуле![]() ,
где
,
где![]() - мощность входного алфавита
- мощность входного алфавита![]() .
Если
.
Если![]() ,
то
,
то![]() ,
т.е. каждая буква
,
т.е. каждая буква![]() кодируется двоичным вектором, состоящим
из двух компонент, например
кодируется двоичным вектором, состоящим
из двух компонент, например![]() .
Минимальное число элементарных выходных
каналов
.
Минимальное число элементарных выходных
каналов![]() .
Для множества состояний
.
Для множества состояний![]()
![]() .
.
Процесс замены букв алфавита
![]() абстрактного автомата двоичными
векторами называется кодированием и
может быть описан таблицами кодирования.
абстрактного автомата двоичными
векторами называется кодированием и
может быть описан таблицами кодирования.
Пример: Абстрактный автомат Мили задан
совмещенной таблицей переходов-выходов
1. Кодирование букв алфавита
![]() ,
представлено таблицами 2, 3, 4. При этом
,
представлено таблицами 2, 3, 4. При этом![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
|
Таблица 1
|
Таблица 2 вх. сигн. код
|
Таблица 3 вых. сигн. код
|
Таблица 4 состояния код
|
Таблица 5
|
|
|
входные сигналы | |
|
|
|
| |
|
состояния |
|
|
|
|
01 |
|
| |
|
|
10/00 |
| |
Каждой кодируемой букве может быть приписан произвольный двоичный вектор, но обязательно две различные буквы (одного алфавита) должны кодироваться различными двоичными векторами. Получением структурной таблицы переходов-выходов автомата (табл. 5) заканчивается это кодирование.
