8.1 Метод Квайна

Метод применим к СДНФ и основывается на применении двух основных соотношений:

1. склеивание

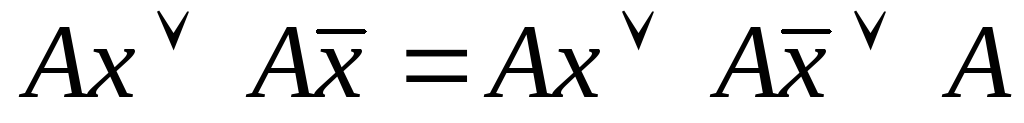
2. поглощение

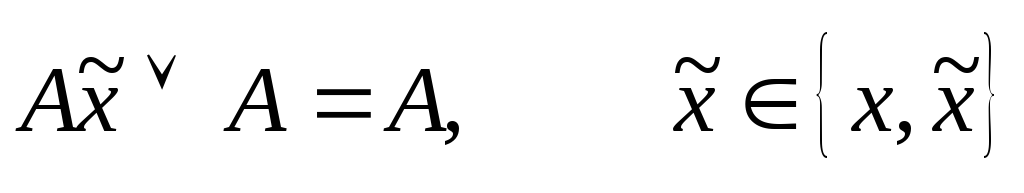
Суть метода заключается в последовательном выполнении всех возможных склеиваний и затем всех поглощений, что приводит к СкДНФ.

Для получения МДНФ необходимо убрать из СкДНФ все лишние простые импликанты с помощью импликантной матрицы Квайна. В строках матрицы отмечаются простые импликанты, а в столбцах – конституэнты "1" булевой функции. Минимальные ДНФ строятся по импликантной матрице таким образом:

1. ищутся столбцы матрицы, имеющие только один крестик. Соответствующие этим крестикам простые импликанты называются базисными и составляют ядро булевой функции. Ядро обязательно входит в МДНФ.

2. рассматриваются различные варианты выбора совокупности простых импликант, которые накроют крестиками остальные столбцы матрицы, и выбираются варианты с минимальным суммарным числом букв в такой совокупности импликант.

Пример: .

1. Избавимся от отрицаний и скобок:

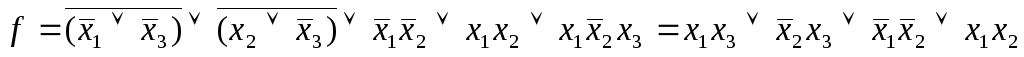
2. Восстановим СДНФ, применяя развертывание:

3. Найдем СкДНФ, произведя все возможные склеивания:

4. Ищем МДНФ:

импликанты	Конституэнты "1"
				Я	Я

Ядро: мднф:

8.2 Метод Квайна-Мак-Класки

Метод формализован на этапе нахождения простых импликант. Формализация проводится таким образом:

1. Все конституэнты "1" из СДНФ булевой функции записываются их двоичными номерами.

2. Все номера разбиваются на непересекающиеся группы, в i-ой группе находятся конституэнты "1", содержащие i единиц в номере.

3. Склеиваются только номера соседних групп, склеивание номера как-либо отмечают.

4. Производят все возможные склеивания. Неотмеченные после склеивания номера являются простыми импликантами.

Пример:

1. В СДНФ заменим все конституэнты "1" их двоичными номерами:

2. Образуем группы двоичных номеров и произведем склеивание:

номер группы	двоичные номера конституэнт "1"		номер группы	двоичные номера конституэнт "1"		номер группы	двоичные номера конституэнт "1"
0 1 2 3 4	- 0001 0011,0101 0111,1110 1111		1 2 3	00*1,0*01 0*11,01*1 *111, 111*		1	0**1

		0001	0011	0101	0111	1110	1111
0**1
*111
111*

Простые импликанты: *111, 111*, 0**1

МДНФ:

Разбиение конституэнт на группы позволяет уменьшить число парных сравнений при склеивании.