8.6 Минимизация монотонных функций

Для монотонных функций СкДНФ совпадает с минимальной, что следует из теоремы: для того, чтобы булева функция Ж была монотонной, необходимо и достаточно, чтобы ее СкДНФ не содержала отрицаний переменных. СкДНФ является и МДНФ булевой функции.

Для получения МДНФ монотонных функций могут быть использованы все методы нахождения СкДНФ произвольных булевых функций.

8.7 Минимизация конъюнктивных нормальных форм

Минимизация КНФ проводится аналогично минимизации ДНФ булевых функций. Конституэнта "0" – функция = 0 на одном наборе.

Определение: Имплицентой булевой функции называется функция, принимающая значение 0 на подмножестве нулевых наборов функции .

Простой имплицентой функции называется элементарная дизъюнкция, являющаяся имплицентой функции , причем никакая ее собственная часть уже имплицентой функции не является.

Задача минимизации КНФ – определение МКНФ – решается в два этапа: поиск СкКНФ (конъюнкция всех простых имплицент) и затем нахождение МКНФ с помощью таблицы Квайна, где рассматривается, поглощает ли данная простая имплицента конституэнту "0" или нет в соответствии с соотношением поглощения:

Для первого этапа: соотношения склеивания по Квайну

Метод Нельсона в применении к задаче минимизации КНФ: раскрытие скобок в произвольной ДНФ функции и выполнение поглощений приводит к СкКНФ. Предполагаются скобки в начале и в конце каждого элементарного произведения исходной ДНФ и использование второго дистрибутивного закона.

Пример: функция, заданная МДНФ дает возможность определить ее СкКНФ:

По диаграмме Вейча для поиска МКНФ анализируются лишь нулевые наборы и переменные выписываются с инверсиями:

МKНФ:

МДНФ:

8.8 Минимизация частично определенных булевых функций

В реальных задачах часто бывает так, что значение булевой функции на некоторых наборах не определено и может доопределяться произвольно. Тогда доопределение функции целесообразно проводить так, чтобы ее минимальная нормальная форма имела наименьшее число букв из всех возможных вариантов доопределения.

Алгоритм поиска МДНФ частично определенной функции:

1. найти любым способом СкДНФ функции, получающуюся доопределением единицами исходной функции на всех неопределенных наборах;

2. выбрать МДНФ по импликантной матрице, где в столбцах выписаны лишь те конституэнты "1" функции 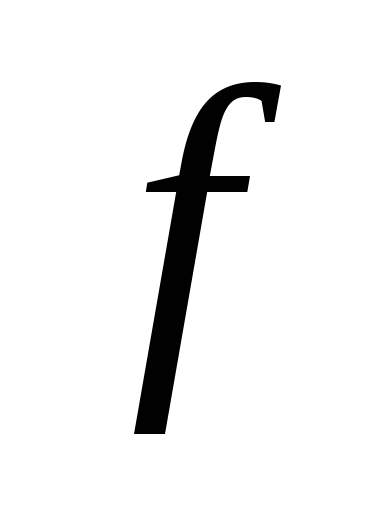, которые соответствуют полностью определенным единичным наборам.

По диаграмме Вейча:

ДНФ: ДНФ:

КНФ: КНФ:

ДНФ: КНФ:

8.9 Минимизация функций в базисах и-не и или-не

Функции " стрелка Пирса" (ИЛИ-НЕ) и "штрих Шеффера" (И-НЕ) обладают функциональной полнотой; для двух переменных:

Для n переменных:

Эти соотношения позволяют свести задачу минимизации булевой функции в рассматриваемых базисах к задаче минимизации ДНФ и КНФ.

Для того, чтобы перейти от КНФ функции к выражению, представляющему функциюс помощью операции "стрелка Пирса" достаточно заменить в КНФ все операции конъюнкции и дизъюнкции операцией, сохранив скобки и отрицания на своих местах.

КНФ функции можно представить в общем виде:

где – элементарные дизъюнкции : ;

Используя операцию для nпеременных, получим:

Таким образом, минимизацию функции можно осуществлять в базисе , а затем перейти к операции. Операция с помощьюреализуется таким образом:

При переходе от многоместных операций к двухместным, необходимо учитывать, что функции и / не подчиняются закону ассоциативности (;). Если элементы только двухвходовые, то можно использовать следующие переходные соотношения:

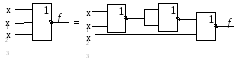Пример: рассмотрим функцию, заданную диаграммой Вейча:

МКНФ:

Переходя к двухместным операциям, получаем:

Аналогично осуществляется переход от произвольной ДНФ к выражению, содержащему только операцию "штрих Шеффера". Справедливы также переходные соотношения:

Пример:

МДНФ: