
- •Министерство образования и науки украины
- •Содержание
- •Глава 1 Арифметико-логические основы эвм
- •1.1 Информационные процессы
- •1.2. Обмен информацией между различными информационными устройствами
- •1.3. Аппаратные средства хранения и обработки информации
- •Глава 2 представление числовой информации в цифровом автомате
- •2.1. Системы счисления и понятие кода
- •2.2. Выбор системы счисления
- •2.3. Формальные правила двоичной арифметики
- •2.4. Перевод числа из одной позиционной системы счисления в другую
- •Глава 3 формы представления чисел в цифровых автоматах
- •3.1. Форма представления двоичных чисел с фиксированной запятой
- •3.2. Представление отрицательных чисел в формате с фиксированной запятой
- •3.3. Форма представление чисел с плавающей запятой
- •3.4. Перевод чисел из формата с фиксированной запятой в формат с плавающей запятой и обратно
- •3.5. Погрешности представления чисел
- •20 [A]ф2n- 1 для целых чисел
- •Глава 4. Арифметические действия с двоичными числами
- •4.1. Сложение двоичных чисел
- •4.1.1. Алгебраическое сложение чисел, представленных в форме с фиксированной запятой
- •4.1.2. Переполнение разрядной сетки
- •4.1.3. Модифицированный прямой, обратный и дополнительный код
- •4.1.4. Алгебраическое сложение чисел, представленных в форме с плавающей запятой
- •4.2. Умножение двоичных чисел
- •4.2.1. Методы умножения двоичных чисел
- •4.2.2. Умножение чисел, представленных в форме с фиксированной запятой
- •4.2.3. Умножение чисел, представленных в форме с плавающей запятой
- •4.2.4. Ускорение операции умножения
- •4.3. Деление двоичных чисел
- •4.3.1. Деление двоичных чисел, представленных в форме с фиксированной запятой.
- •4.3.2. Деление двоичных чисел, представленных в форме с плавающей запятой.
- •4.4. Оценка точности выполнения арифметических операций
- •4.4.1. Погрешность округления
- •Глава 5. Выполнение операций над двоично-десятичными числами
- •5.1. Представление десятичных чисел в д-кодах
- •5.2. Формальные правила поразрядного сложения в д-кодах
- •5.3. Представление отрицательных чисел в д-кодах
- •5.4. Выполнение операций сложения и вычитания в д-кодах
- •5.5. Умножение чисел в д-кодах
- •5.6. Деление чисел в д-кодах
- •5.7. Перевод чисел из д-кода в двоичный и из двоичного в д-код
- •Глава 6 Информационные основы цифровых автоматов
- •6.1. Понятие об информации и её преобразованиях
- •6.2. Преобразования алфавитной информации
- •6.3 Понятие об алгоритме
- •6.4 Понятие о дискретном (цифровом) автомате
- •Глава 7 Основы логического проектирования ца. Основные понятия алгебры логики.
- •7.1. Свойства элементарных функций алгебры логики
- •7.2. Аналитическое представление функций алгебры логики
- •7.3. Совершенные нормальные формы
- •7.4. Системы функций алгебры логики
- •7.5. Числовое и геометрическое представление фал
- •Глава 8 Минимизация функций алгебры логики
- •8.1 Метод Квайна
- •Ядро: мднф:
- •8.2 Метод Квайна-Мак-Класки
- •Простые импликанты: *111, 111*, 0**1
- •8.3 Метод Нельсона
- •8.4 Метод диаграмм Вейча
- •8.5 Метод самопонижающихся циклов
- •8.6 Минимизация монотонных функций
- •8.7 Минимизация конъюнктивных нормальных форм
- •8.8 Минимизация частично определенных булевых функций
- •8.9 Минимизация функций в базисах и-не и или-не
- •8.10 Минимизация систем булевых функций
- •Глава 9 Абстрактная теория автоматов
- •9.2 Декомпозиция абстрактных автоматов
- •Глава 10 Структурная теория автоматов
- •10.1 Композиция автоматов
- •Глава 11 Проектирование асинхронных цифровых автоматов
- •11.1 Проектирование комбинационных схем (кс) с учетом кобъед по входу и по выходу
- •11.2 Проектирование кс на дешифраторах и мультиплексорах
- •11.3 Проектирование кс на пзу
- •11.4 Проектирование кс на плм
- •Глава 12 Канонический метод структурного синтеза ца с памятью
- •12.1 Кодирование
- •12.2 Выбор элементов памяти автомата
- •12.3 Выбор структурно-полной системы элементов
- •12.4 Построение уравнений булевых функций возбуждения и выходов автомата
- •12.5 Построение функциональной схемы автомата
- •Глава 13 Обеспечение устойчивости функционирования ца
- •13.2 Проблема синтеза надёжных схем из ненадёжных элементов
- •13.3 Коды Хэмминга
- •Глава 14 Микропрограммные автоматы
- •14.2 Граф-схемы алгоритмов
9.2 Декомпозиция абстрактных автоматов
Под декомпозицией понимается представление абстрактного автомата совокупностью нескольких более простых автоматов.
Задача декомпозиции абстрактного автомата – это задача разложения автомата по алгебраическим операциям. В качестве операций обычно рассматриваются такие: умножение, суммирование, суперпозиция и композиция.
Рассмотри задание алгебраических операций умножения, суммирования, суперпозиции автоматов.
О перация
умножения двух автоматов А1и А2содержательно соответствует параллельной
одновременной работе автоматов А1и А2, т.е. подача на вход автомата
А3входного сигнала
перация
умножения двух автоматов А1и А2содержательно соответствует параллельной
одновременной работе автоматов А1и А2, т.е. подача на вход автомата
А3входного сигнала![]() соответствует тому, что на входы автоматов
А1и А2одновременно и
независимо друг от друга подаются
входные сигналы
соответствует тому, что на входы автоматов
А1и А2одновременно и
независимо друг от друга подаются
входные сигналы![]() и
и![]() .
.
Различают две модификации операции
умножения. Первая,
![]() ,
применяется к абстрактным автоматам
А1и А2с различными входными
алфавитами. Вторая,
,
применяется к абстрактным автоматам
А1и А2с различными входными
алфавитами. Вторая,![]() ,
применяется к абстрактным автоматам
А1и А2, имеющим общий входной
алфавит, и является частным случаем
операции умножения.
,
применяется к абстрактным автоматам
А1и А2, имеющим общий входной
алфавит, и является частным случаем
операции умножения.
Пример: Пусть автоматы А1и А2заданы графами.
Так как операция
![]() соответствует одновременной параллельной
работе двух А1и А2с раздельными
входами, то построение графа А3можно описать таким образом: каждое
с
соответствует одновременной параллельной
работе двух А1и А2с раздельными
входами, то построение графа А3можно описать таким образом: каждое
с остояние
автомата А3будет однозначно
соответствовать упорядоченной паре
состояний автоматов А1и А2.
В начальный момент времени А3будет иметь состояние
остояние
автомата А3будет однозначно
соответствовать упорядоченной паре
состояний автоматов А1и А2.
В начальный момент времени А3будет иметь состояние![]() .
Осуществляя перебор всех возможных
комбинаций пар входных сигналов автоматов
А1и А2, получаем все возможные
переходы автомата А3.
.
Осуществляя перебор всех возможных
комбинаций пар входных сигналов автоматов
А1и А2, получаем все возможные
переходы автомата А3.

Операция суммирования + двух автоматов А1и А2соответствует параллельной неодновременной работе автоматов А1и А2; т.е. если задан автомат А3=А1+А2, то любое входное слово автомата А3образуется чередованием входных букв А1и А2, а любое выходное слово – чередованием выходных букв А1и А2.
Д ля
автоматов А1и А2, приведенных
выше, операция + будет представлена
следующим образом:
ля
автоматов А1и А2, приведенных
выше, операция + будет представлена
следующим образом:

Операция суперпозиции
![]() соответствует последовательной работе
автоматов А1и А2
соответствует последовательной работе
автоматов А1и А2
Построим автомат А3=А1*А2

Глава 10 Структурная теория автоматов
10.1 Композиция автоматов
Главная отличительная особенность структурной теории автоматов состоит в том, что, в отличие от абстрактной теории, она учитывает структуру входных и выходных сигналов автомата, а также его внутреннюю структуру на уровне так называемых структурных схем. Основной задачей структурной теории автоматов является изучение композицииавтоматов, т.е. методов построения сложных автоматов из автоматов, являющихся относительно простыми.
Структурная теория автоматов не ставит своей задачей отразить все свойства реально существующих автоматов. В ней, например, совершенно не учитываются переходныепроцессыв автоматах, вопросы надежности работы автоматов, физические свойства сигналов и др.
Структурная теория автоматов и абстрактная теория автоматов являются двумя различными частями общей теории автоматов. При синтезе реальных автоматов многие вопросы проще и эффективнее решаются на уровне абстрактной теории. К числу таких вопросов относится определение необходимого объема памятиавтомата(т.е. числа его состояний), переходов в памяти, а также вопросы, относящиеся к минимизации числа состояний автомата. В то же время имеется ряд вопросов – таких, например, как вопрос о композиции автоматов, - сама постановка которых выводит за рамки абстрактной теории автоматов.
В структурной теории автоматов как входные, так и выходные каналы рассматриваемых автоматов считаются состоящими из нескольких элементарныхвходныхи соответственноэлементарныхвыходныхканалов. По всем элементарным каналам могут передаваться так называемые элементарные сигналы. Набор всех возможных для данного автомата элементарных сигналов называется структурным алфавитом этого автомата.
К аждый
элементарный канал (входной или выходной)
подсоединяется к так называемомуузлу.
Существуют входные узлы автомата и
выходные узлы автомата. В каждом автомате
осуществляется определенная циркуляция
элементарных сигналов. Элементарные
входные сигналы поступают сначала на
входные узлы, а затем по подсоединенным
к ним элементарным входным каналам
передаются внутрь автомата. Элементарные
выходные сигналы, выходя из автомата
по элементарным выходным каналам,
поступают на соответствующие выходные
узлы.
аждый
элементарный канал (входной или выходной)
подсоединяется к так называемомуузлу.
Существуют входные узлы автомата и
выходные узлы автомата. В каждом автомате
осуществляется определенная циркуляция
элементарных сигналов. Элементарные
входные сигналы поступают сначала на
входные узлы, а затем по подсоединенным
к ним элементарным входным каналам
передаются внутрь автомата. Элементарные
выходные сигналы, выходя из автомата
по элементарным выходным каналам,
поступают на соответствующие выходные
узлы.
Сформулируем определение общегоспособакомпозицииавтоматов.
Пусть
![]() (где
(где![]() )
конечное множество автоматов. Произведем
объединение этих автоматов в систему
совместно работающих автоматов следующим
образом.
)
конечное множество автоматов. Произведем
объединение этих автоматов в систему
совместно работающих автоматов следующим
образом.
Введем в рассмотрение некоторое конечное множество узлов, которое назовем внешнимивходнымиузлами, и некоторое конечное множество других узлов, которое назовемвнешнимивыходнымиузлами(полюсами). Эти узлы предполагаются отличными от входных и выходных узлов рассматриваемых автоматов, которые будем называтьвнутренними(входнымиивыходными)узлами.
Композиция автоматов состоит в том, что
в полученной системе, состоящей из
данных автоматов
![]() и внешних узлов, производитсяотождествлениенекоторыхузлов(как внешних,
так и внутренних). С точки зрения
совместной работы системы автоматов
смысл операции отождествления узлов
состоит в том, что элементарный сигнал,
попадающий на один из узлов, входящих
во множество отождествленных между
собой узлов, попадает сразу на все узлы
этого множества. Для электронных ЦА
операции отождествления узлов
соответствует соединение этих узлов
проводниками.
и внешних узлов, производитсяотождествлениенекоторыхузлов(как внешних,
так и внутренних). С точки зрения
совместной работы системы автоматов
смысл операции отождествления узлов
состоит в том, что элементарный сигнал,
попадающий на один из узлов, входящих
во множество отождествленных между
собой узлов, попадает сразу на все узлы
этого множества. Для электронных ЦА
операции отождествления узлов
соответствует соединение этих узлов
проводниками.
В результате проведения операции отождествления (соединения) узлов, все узлы, входящие в данную систему (внутренние и внешние), разобьются на попарно непересекающиеся множества отождествленных между собой узлов.
После проведенных отождествлений
система автоматов превращается в так
называемую схему(сеть) автоматов.
Будем считать, что автоматы, входящие
в схему, работают совместно, если в
каждый момент автоматного времени![]() (
(![]() ) на все внешние входные узлы схемы
подается какой-либо набор элементарных
сигналов (структурный входной сигнал
схемы), а с внешних выходных узлов схемы
снимается получающийся на них набор
элементарных выходных сигналов
(структурный выходной сигнал).
) на все внешние входные узлы схемы
подается какой-либо набор элементарных
сигналов (структурный входной сигнал
схемы), а с внешних выходных узлов схемы
снимается получающийся на них набор
элементарных выходных сигналов
(структурный выходной сигнал).
Предположим, что в каждый момент
дискретного времени
![]() структурный выходной сигнал схемы
однозначно определяется 1) поступившей
к этому времени последовательностью
структурных входных сигналов; 2) начальными
состояниями входящих в схему автоматов
и 3) сделанными при построении схемы
отождествлениями узлов. Построенная
схема может рассматриваться как некоторый
ЦА
структурный выходной сигнал схемы
однозначно определяется 1) поступившей
к этому времени последовательностью
структурных входных сигналов; 2) начальными
состояниями входящих в схему автоматов
и 3) сделанными при построении схемы
отождествлениями узлов. Построенная
схема может рассматриваться как некоторый
ЦА![]() ,
а сама схема называтьсяструктурнойсхемойэтогоавтомата.
,
а сама схема называтьсяструктурнойсхемойэтогоавтомата.
Полученный описанным способом автомат
![]() есть результат композиции исходных
автоматов
есть результат композиции исходных
автоматов![]() .
.
Однако не всякое отождествление узлов приводит к схеме, которую можно рассматривать как структурную схему некоторого автомата. Необходимо соблюдать два условия корректности схемы:
в любой момент времени на каждый узел схемы (как внешний, так и внутренний) поступает какой-либо элементарный сигнал;
неоднозначность элементарных сигналов в каком-нибудь узле схемы хотя бы в один момент времени является недопустимой (существуют два источника неоднозначности элементарного сигнала в узле 1) если к какому-то узлу подсоединено одновременно несколько выходных узлов, являющихся источниками элементарных сигналов; 2) наличие петли или циклической цепи в структурной схеме).
П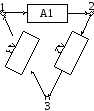 равильнойкомпозициейавтоматовназывается
операция построения схемы автомата,
для которой выполняются три условия:
равильнойкомпозициейавтоматовназывается
операция построения схемы автомата,
для которой выполняются три условия:
Для любого узла схемы должна существовать цепь, состоящая из некоторого множества (м.б. пустого) автоматов Мили, начинающаяся каким-нибудь задающим (внешние входные или внутренние выходные узлы автомата Мура) узлом и кончающаяся узлом (условие передачи элементарных сигналов от задающих узлов на все узлы автомата в каждый момент автоматного времени).
Любой узел схемы должен быть отождествлен (соединен) не более чем с одним внешним входным или внутренним выходным узлом.
Любая нетривиальная (содержащая не менее одного ЦА) петля в схеме должна содержать в своем составе хотя бы один автомат Мура.
