8.10 Минимизация систем булевых функций

Задача минимизации систем булевых функций хорошо исследована в ФПСБФ Рассмотрим один из наиболее распространенных методов минимизации.

Пусть задана система полностью определенных булевых функций в ДНФ, например:

Все различные элементарные конъюнкции систем булевых функций объединим в множество А, которое назовем полным множествомэлементарных конъюнкций системы булевых функций.

Система ДНФ булевых функций называется минимальной, если ее полное множество элементарных конъюнкций содержит минимальное количество букв, а каждая ДНФ булевых функций системы включает минимальное число элементарных конъюнкций наименьшего ранга. минимизация систем полностью определенных булевых функций может производиться по алгоритму, аналогичному алгоритму метода Квайна с небольшими отличиями.

П

x1	x2	x3	f1	f2
0	0	0	1	1
0	0	1	0	0
0	1	0	0	1
0	1	1	0	1
1	0	0	0	0
1	0	1	1	1
1	1	0	1	0
1	1	1	1	0

ример: пусть система булевых функций задана таблицей истинности. Найти МДНФ системы булевых функций.

Представим функции в СДНФ:

1. Построим полное множество А элементарных конъюнкций системы, указывая, какой функции принадлежит каждая конституэнта "1".

2. Построим СДНФ функции , конституэнтами "1" которой являются все элементы множества А. Найдем СкДНФ функции.

Выполним все склеивания:

1-2:

2-3:

4-6:

5-6:

Если конституэнты единицы не принадлежат одной и той же функции системы, склеивание не производится.

Выполним все поглощения с учетом признака принадлежности каждой конъюнкции к функциям системы:

3. Строим импликантную матрицу Квайна.

простые импликанты системы функций
	1	2	2	2	1	2	1	1

- ядро функции :

в данном случае ядро совпадает с МДНФ функции .

МДНФ системы булевых функций:

Недостаток метода: большая трудоемкость операций склеивания и поглощения с признаками.

Глава 9 Абстрактная теория автоматов

Абстрактным автоматом называется дискретное устройство, задаваемое тремя непустыми множествами , , называемыми алфавитами входных сигналов, выходных сигналов и состояний, и двумя функциями - функцией переходов , определяющей состояние автоматав S+1-м такте в зависимости от состояния автоматаи значения входной буквыв S-м такте

и функцией выходов , определяющей значение выходной буквыв зависимости от состояния автоматаи входной буквыв S -м такте

Обычно на множестве фиксируется одно из состоянийв качестве начального (инициальный автомат).

По способу формирования функции выхода выделяют 3 типа абстрактных автоматов: автомат Мили, автомат Мура, С-автомат.

Эти автоматы описываются системой уравнений:

автомат Мили: автомат Мура:

С-автомат:

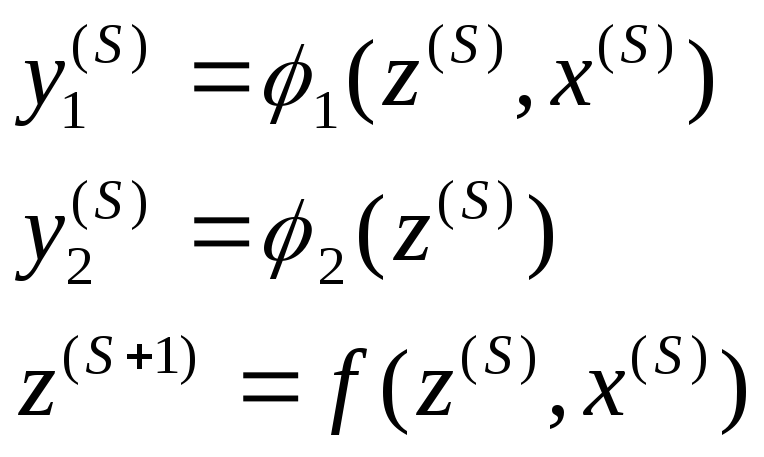
Будем рассматривать только автоматы детерминированного типа, у которых каждой паре иоднозначно соответствует параи. Функционирование детерминированных автоматов подчиняется следующим условиям:

• любому входному слову из 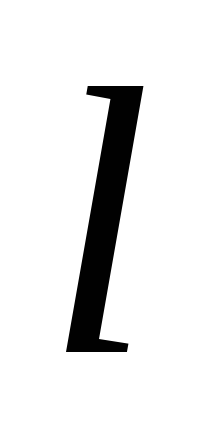букв (слову длиной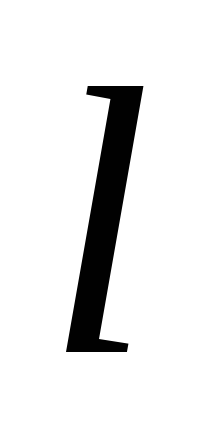) соответствует выходное слово той же длины,

• двум входным словам, в которых первые 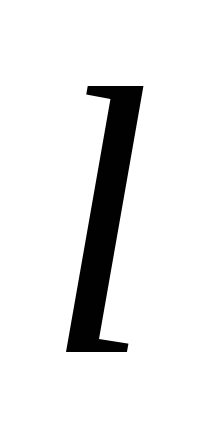букв совпадают, соответствуют выходные слова с совпадающимипервыми буквами, если перед подачей входных слов, автомат находился в одном и том же состоянии.

Ф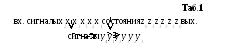ункциии, описывающие работу автомата Мили, можно задать с помощью таблиц переходов и выходов. По этим таблицам можно определить реакцию автомата на любое входное слово.

В таблице 1 приведены произвольная последовательность входных сигналов и соответствующие ей последовательности состояний и выходных сигналов автомата, заданного таблицей переходов и выходов.

Б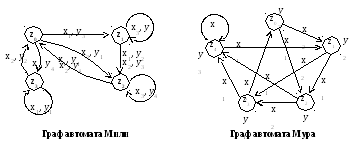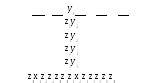олее наглядным является представление автоматов Мили с помощью графов. Граф автомата состоит из узлов (вершин) соединенных ветвями (ребрами). Узлы графа отождествляются с состояниями автомата, а ветви отмечаются входными сигналами, вызывающими переход автомата по данной ветви, и выходными сигналами, соответствующими такому переходу.

Два автомата, у которых совпадают как входные, так и выходные сигналы, называются эквивалентными. если для любого входного слова выходное слово одного автомата совпадает с выходным словом другого автомата.

Для любого автомата Мили можно построить эквивалентный автомат Мура и наоборот. Для этого:

1. поставим каждой паре 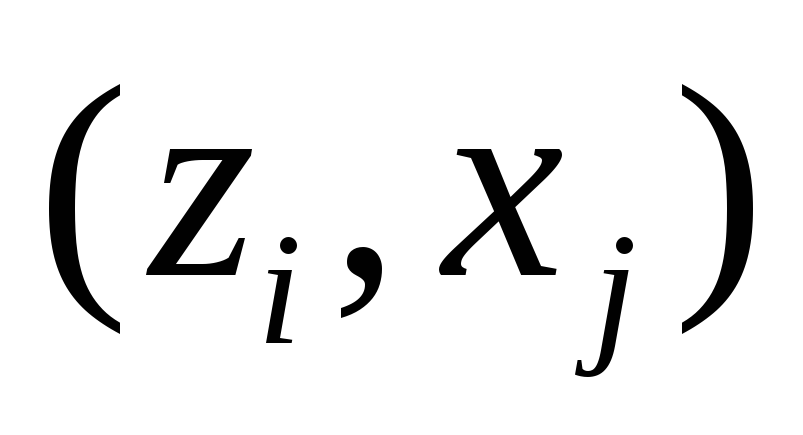автомата Мили состояниеавтомата Мура;

2. во множество состояний автомата Мура включим начальное состояние автомата Мили. Если автомат Мили имеетсостояний и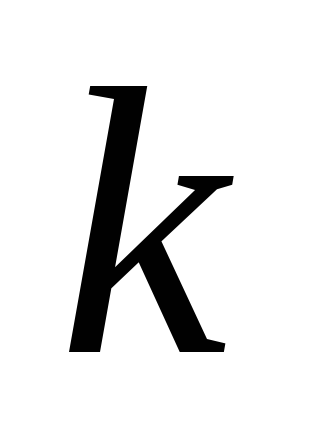входных сигналов, то эквивалентный автомат Мура будет иметьсостояний.

И

	z0 z00	z1	z2	z3
x1	z1 z01	z2 z11	z0 z21	z3 z31
x2	z3 z02	z2 z12	z0 z22	z0 z32
x3	z2 z03	z1 z13	z2 z23	z3 z33

з таблицы видно, что состояниеавтомата Мили совпадает с состояниямиавтомата Мура, т.е.

, ,

Значения функции выходов для эквивалентного автомата Мура определяются соотношением:

при

Для начального состояния значение выходного сигнала выбирается произвольно. Т.о. переходы и выходные сигналы эквивалентного автомата Мура определяются таблицей:

Задача перехода от автомата Мура к эквивалентному автомату Мили решается очень просто. Если и– функции переходов и выходов автомата Мура, то функции переходови выходовэквивалентного автомата Мили определяются соотношениями:

;

Т.о. таблица переходов эквивалентного автомата Мили совпадает с таблицей переходов автомата Мура, а таблица выходов составляется так, что в каждую ее клетку записывается сигнал, которым отмечено состояние в данной клетке.

Частичными автоматами называются автоматы, на входы которых некоторые последовательности сигналов никогда не подаются (запрещенные входные слова)

Основными задачами теории автоматов являются задачи анализа и синтеза автоматов. Под анализом автомата понимают установление закона его функционирования по заданной схеме автомата, под синтезом – построение автомата из более простых автоматов по заданному закону функционирования. При решении этих задач наиболее важными являются абстрактный и структурный этап.

На абстрактном этапе автомат задается таблицами или графом или каким-нибудь другим способом. На структурном этапе автомат понимают как структурную схему, состоящую из набора простейших автоматов и ФПС логических элементов.