11.2 Проектирование кс на дешифраторах и мультиплексорах

Дешифратор (DC) – это КС, реализующая все конституэнты "1" или схема, имеющая nвходов ивыходов, включающая один из выходных каналов при подаче соответствующего входного набора.

Рассмотри два способа синтеза дешифратора: матричный и прямоугольный.

При синтезе DC используют только элементы И или ИЛИ-НЕ:

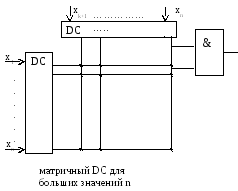
Имея DC можно реализовать произвольную булеву функцию, объединив с помощью схемы ИЛИ те его выходы, которые соответствуют «1» в таблице истинности. Для этой цели можно использовать мультиплексор (MUX).

Под MUX понимают конструктивный элемент с одним выходом и двумя группами входов: адресные входы (входы управления, селекторные) и входы данных. MUX позволяет подачей двоичного набора на адресные входы подключать к выходу требуемый вход данных. Т.е. MUX является коммутатором соответствующего входа данных на свой выход.

0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Если на входы данных подать двоичный набор, соответствующий столбцу значений функцииf, а на адресные входы – значения переменных, то MUX реализует функцию заданную таблицей.

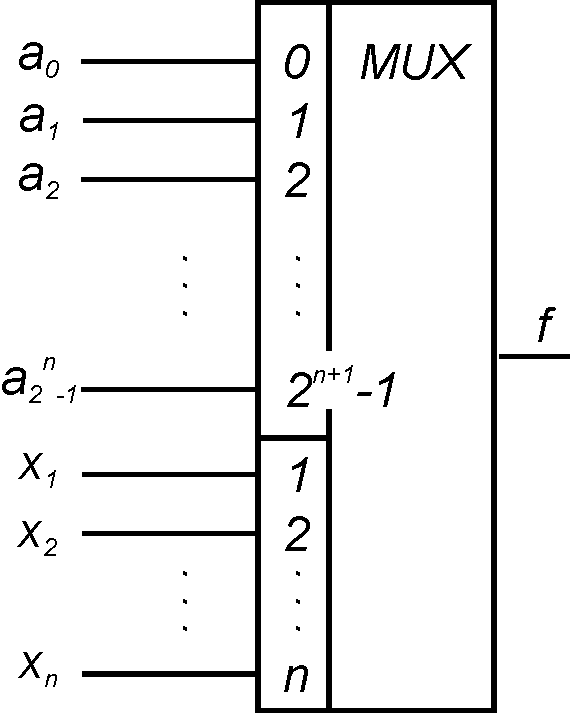
Если MUX имеет n-адресных входов, то на таком MUX можно реализовать любую булеву функцию от (n+1) для этого представим функциюее таблицей истинности. Переменныевыделим как адресные, а переменную- как переменную данных MUX. Тогда возможны 4 ситуации для любых двух соседних наборов длины (n+1) с одинаковой адресной частью:

1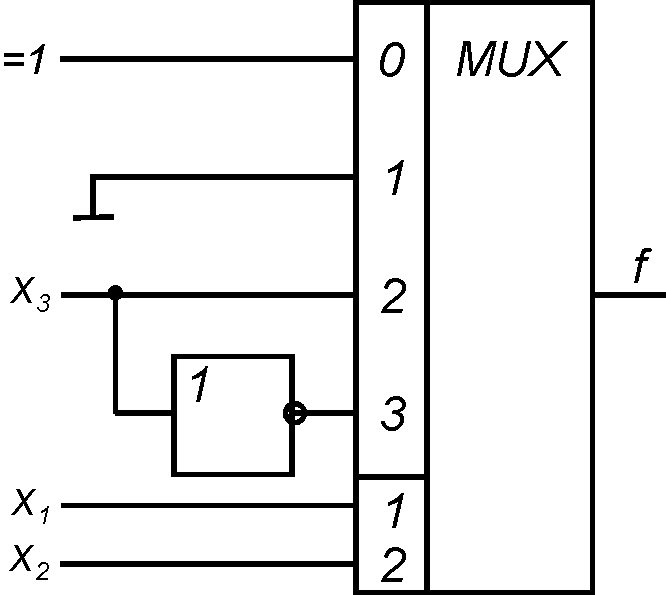); 2); 3); 4).

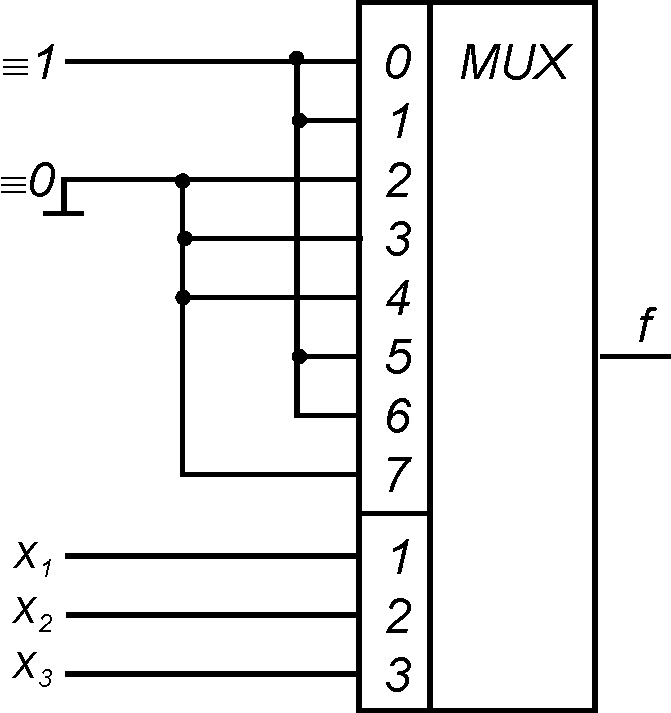
Пример: Для функции от 3х переменных, приведенной в табличной форме имеем следующее. Переменные и- выделим как адресные. Тогда если на адресные входы поступает набор 1), то; 2), то; 3), то; 4), то.

Можно использовать MUX для реализации булевых функций большого числа переменных. Для этого производят разложение функции от nпеременных по переменным

где , а реализуется отдельнымиMUX_iи подключается ко входам данных MUX для переменных . Рассмотрим пример реализации функции от 5 переменных.

11.3 Проектирование кс на пзу

(Краткая информация о ПЗУ и ППЗУ.)

Любое ПЗУ имеет nвходов (адресных) иkвыходов. Если, а, то ПЗУ содержитячеек памяти, в каждую из которых может быть записано слово длиной в 2 бита.

ПЗУ можно использовать не только для хранения информации, но и для ее обработки. Они могут быть использованы для реализации булевых функций, построения устройств управления различного назначения и т.д.

Рассмотрим проектирование КС на ПЗУ.

Пусть есть булевых функций отпеременных, представленных таблицами истинности. В ячейку памяти с нулевым адресом некоторого ПЗУ запишем значения функций из первой строки правой части таблицы истинности, в ячейку с адресом- значения функций из второй строки таблицы истинности и т.д. Если теперь на адресные входы ПЗУ (;) подать набор, то на выходах ПЗУ появятся значения функций на наборе.

Если , а , то для реализации системы булевой функций необходимо разбить её на подсистемы, каждая из которых содержит не болееk функций и может быть реализована на одной схеме ПЗУ. Если , то могут быть использованы различные приёмы декомпозиции булевых функций по переменным, с реализацией получаемых подфункций на ПЗУ и последующим объединением выходов ПЗУ через различные элементы. Пусть существует система булевой функцийот 4-х переменных, заданная таблицей истинности; её реализация на К155ПР6.

0	0	0	0	0	0	1
0	0	0	1	0	1	0
0	0	1	0	1	0	0
0	0	1	1	1	0	1
0	1	0	0	0	0	0
0	1	0	1	0	1	1
0	1	1	0	1	1	0
0	1	1	1	0	0	1
1	0	0	0	0	1	1
1	0	0	1	1	1	1
1	0	1	0	0	0	1
1	0	1	1	0	1	0
1	1	0	0	0	1	0
1	1	0	1	0	1	0
1	1	1	0	1	0	1
1	1	1	1	1	0	1

Более общий способ синтеза КС, реализующий булевы функции с применением ПЗУ и MUX, заключается в следующем.

Производят разложение булевых функций по kпеременных, гдеk- число адресных входов MUX. Оставшиеся2^kфункций от (n-k) переменных реализуют, используя ПЗУ, после чего подключают выходы ПЗУ к входам данных MUX в соответствии с формулой разложения заданной функции. При этом дизъюнктивные члены разложения будут иметь вид:

,

где .

Пример:

э

Запишем f в виде:

0	0				1 х
1	1				х 1
0	1					1 1
0	1					1 х
1	0					х 1
1	0					1 1

Здесь число переменных. Используя MUX с двумя адресными входами и ПЗУ с тремя адресными входами и двумя выходами построим схему:

Схема реализации функции от пяти переменных.