
- •Министерство образования и науки украины
- •Содержание
- •Глава 1 Арифметико-логические основы эвм
- •1.1 Информационные процессы
- •1.2. Обмен информацией между различными информационными устройствами
- •1.3. Аппаратные средства хранения и обработки информации
- •Глава 2 представление числовой информации в цифровом автомате
- •2.1. Системы счисления и понятие кода
- •2.2. Выбор системы счисления
- •2.3. Формальные правила двоичной арифметики
- •2.4. Перевод числа из одной позиционной системы счисления в другую
- •Глава 3 формы представления чисел в цифровых автоматах
- •3.1. Форма представления двоичных чисел с фиксированной запятой
- •3.2. Представление отрицательных чисел в формате с фиксированной запятой
- •3.3. Форма представление чисел с плавающей запятой
- •3.4. Перевод чисел из формата с фиксированной запятой в формат с плавающей запятой и обратно
- •3.5. Погрешности представления чисел
- •20 [A]ф2n- 1 для целых чисел
- •Глава 4. Арифметические действия с двоичными числами
- •4.1. Сложение двоичных чисел
- •4.1.1. Алгебраическое сложение чисел, представленных в форме с фиксированной запятой
- •4.1.2. Переполнение разрядной сетки
- •4.1.3. Модифицированный прямой, обратный и дополнительный код
- •4.1.4. Алгебраическое сложение чисел, представленных в форме с плавающей запятой
- •4.2. Умножение двоичных чисел
- •4.2.1. Методы умножения двоичных чисел
- •4.2.2. Умножение чисел, представленных в форме с фиксированной запятой
- •4.2.3. Умножение чисел, представленных в форме с плавающей запятой
- •4.2.4. Ускорение операции умножения
- •4.3. Деление двоичных чисел
- •4.3.1. Деление двоичных чисел, представленных в форме с фиксированной запятой.
- •4.3.2. Деление двоичных чисел, представленных в форме с плавающей запятой.
- •4.4. Оценка точности выполнения арифметических операций
- •4.4.1. Погрешность округления
- •Глава 5. Выполнение операций над двоично-десятичными числами
- •5.1. Представление десятичных чисел в д-кодах
- •5.2. Формальные правила поразрядного сложения в д-кодах
- •5.3. Представление отрицательных чисел в д-кодах
- •5.4. Выполнение операций сложения и вычитания в д-кодах
- •5.5. Умножение чисел в д-кодах
- •5.6. Деление чисел в д-кодах
- •5.7. Перевод чисел из д-кода в двоичный и из двоичного в д-код
- •Глава 6 Информационные основы цифровых автоматов
- •6.1. Понятие об информации и её преобразованиях
- •6.2. Преобразования алфавитной информации
- •6.3 Понятие об алгоритме
- •6.4 Понятие о дискретном (цифровом) автомате
- •Глава 7 Основы логического проектирования ца. Основные понятия алгебры логики.
- •7.1. Свойства элементарных функций алгебры логики
- •7.2. Аналитическое представление функций алгебры логики
- •7.3. Совершенные нормальные формы
- •7.4. Системы функций алгебры логики
- •7.5. Числовое и геометрическое представление фал
- •Глава 8 Минимизация функций алгебры логики
- •8.1 Метод Квайна
- •Ядро: мднф:
- •8.2 Метод Квайна-Мак-Класки
- •Простые импликанты: *111, 111*, 0**1
- •8.3 Метод Нельсона
- •8.4 Метод диаграмм Вейча
- •8.5 Метод самопонижающихся циклов
- •8.6 Минимизация монотонных функций
- •8.7 Минимизация конъюнктивных нормальных форм
- •8.8 Минимизация частично определенных булевых функций
- •8.9 Минимизация функций в базисах и-не и или-не
- •8.10 Минимизация систем булевых функций
- •Глава 9 Абстрактная теория автоматов
- •9.2 Декомпозиция абстрактных автоматов
- •Глава 10 Структурная теория автоматов
- •10.1 Композиция автоматов
- •Глава 11 Проектирование асинхронных цифровых автоматов
- •11.1 Проектирование комбинационных схем (кс) с учетом кобъед по входу и по выходу
- •11.2 Проектирование кс на дешифраторах и мультиплексорах
- •11.3 Проектирование кс на пзу
- •11.4 Проектирование кс на плм
- •Глава 12 Канонический метод структурного синтеза ца с памятью
- •12.1 Кодирование
- •12.2 Выбор элементов памяти автомата
- •12.3 Выбор структурно-полной системы элементов
- •12.4 Построение уравнений булевых функций возбуждения и выходов автомата
- •12.5 Построение функциональной схемы автомата
- •Глава 13 Обеспечение устойчивости функционирования ца
- •13.2 Проблема синтеза надёжных схем из ненадёжных элементов
- •13.3 Коды Хэмминга
- •Глава 14 Микропрограммные автоматы
- •14.2 Граф-схемы алгоритмов
4.2.3. Умножение чисел, представленных в форме с плавающей запятой
При операции умножения чисел, представленных в форме с плавающей запятой их мантиссы умножаются, как числа с фиксированной запятой, а порядки складываются. В обоих случаях проверка на переполнение обязательна. Но, т.к. реально складываются характеристики чисел, то умножение выполняется по следующей формуле:
A1xA2
=m12![]() xm22
xm22![]() = (m1xm2)2
= (m1xm2)2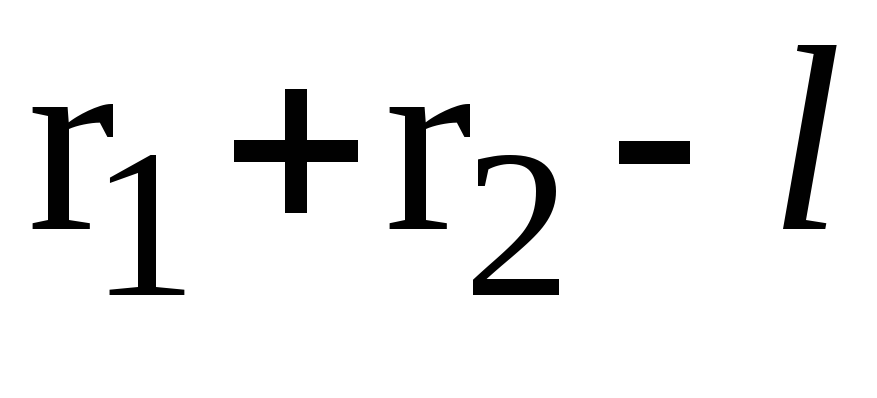 ,
,
где r1 +r2 -l- характеристика результата.
Знак ответа определяется обычным образом. Если ответ получился ненормализованный, то выполняются процедуры нормализации и округления ответа.
Напомним, что при реализации алгоритмов математических операций в формате с плавающей запятой каждый раз, когда осуществляется та или иная процедура, затрагивающая характеристики операндов или результата, производится контроль над переполнением и исчезновением порядка, т.е. контролируется условие
0 r rmax ,
где rmax = l + pmax .
Рассмотрим пример:
умножим числа с мантиссами m1 = 0,101 (5),m2 = 0,1 (2) и характеристиками
r1 = 1011,r2 = 1010,l= 1000,p1 = 3,p2 = 2,p=p1 +p2 = 5,r=r1 +r2 -l= 001011 + 001010 - 001000 = 001101 = 1310m=m1xm2 = 0,01010, необходимо нормализовать ответ. Для этого в данном случае сдвигаем мантиссу влево на 1 разряд и вычитаем 1 изp, получаемp= 4. В итоге имеемm= 0,10102,p= 410 = 01002,r= 1210 = 11002.
4.2.4. Ускорение операции умножения
По времени выполнения операция умножения относится к длинным операциям. Затраты времени на умножение двух чисел в прямом коде можно оценить следующей формулой (для случая последовательного анализа разрядов множителя):
![]() ,
,
где tсдв - время выполнения сдвига числа на один разряд;tсл - время суммирования на сумматоре;pi- вероятность появления единицы в разрядах множителя;n- количество разрядов множителя.
Существуют несколько методов ускорения процедуры умножения: анализ двух разрядов множителя одновременно, анализ произвольного количества разрядов множителя, умножение в системе счисления с основанием q=2kи матричные методы умножения.
Рассмотрим первый спосо, ускорения умножения как наиболее наглядный и распространенный для целых чисел, представленных в прямом коде. В связи с тем, что в этом случае в процессе выполнения операции умножения на каждом цикле операции анализируется сразу два разряда множителя, то таких циклов понадобится n/2, гдеn- длина разрядной сетки множителя без учета знакового разряда. Это число циклов записывается в некоторый счетчикSС. При обнулении содержимого счетчикаSС процедура умножения останавливается. Обычно анализируются два младших разряда множителя, поЭтому в конце каждого цикла производится одновременный сдвиг на два разряда вправо изображения суммы частных произведений (Р) и множителя. Причем, таким образом, чтобы при каждом таком сдвиге очередной младший разряд числа Р попадал в старший разряд мантиссы множителя. Обозначим эту процедуру условно как ПС. Очевидно, что в таком случае произведение будет сформировано в разрядной сетке первоначально отведенной для множителя.
Если множимое Xи множительY, а его два очередных младших разряда (y1y0), то в зависимости от результата анализа этих разрядов предусматриваются следующие действия.
Если y1y0 = 00, то выполняются только процедуры: ПС иSС =SС-1.
Если y1y0 = 01, то выполняются процедуры: Р =P+X, ПС иSС =SС-1.
Если y1y0 = 10, то выполняются процедуры: сдвиг множимого влево на 1 разряд, т.е. умножение его на два,P=P+X, ПС иSС =SС-1.
Если y1y0 = 11, то выполняются три разаP=P+Xи ПС,SС =SС-1.
Когда SС = 0 - операция умножения заканчивается.
Как обычно перед началом самой процедуры умножения определяется знак произведения, проверяются на 0 XиY, если кто-нибудь из них равен 0, то произведению сразу присваивается нулевое значение.
Рассмотрим пример ускоренного умножения 310 на 7810, т.е. когда X= 3, а
Y= 78. Еслиn= 10, тоX= 0000000112,Y= 00010011102, аSС = 5.
512 256 128 64 32 16 8 4 2 1
X00 00 00 00 11 множимое
Y00 01 00 11 10 множитель
R00 11 10 10 10 ответ = 234
В некотором регистре Pбудем формировать частные произведения.
1) Анализ 2-х младших разрядов Y.y1y0 = 10. СдвинутьXна 1 разряд влево и прибавить кP.
P00 00 00 00 00
+X 00 00 00 01 10
P00 00 00 01 10 сдвиг на 2 разрядаPиY
P00 00 00 00 01 ---- 10 00 01 00 11Y
2) y1y0 = 11, _ 3 раза прибавляемXкP
P00 00 00 00 01
+X 00 00 00 00 11
P00 00 00 01 00
+X 00 00 00 00 11
P00 00 00 01 11
+X 00 00 00 00 11
P00 00 00 10 10 сдвиг на 2 разрядаPиY
P00 00 00 00 10 ---- 10 10 00 01 00Y
3) y1y0 = 00, сдвиг на 2 разрядаPиY
P00 00 00 00 00 --- 10 10 10 00 01Y
4) y1y0 = 01
P00 00 00 00 00
+X 00 00 00 00 11
P00 00 00 00 11 сдвиг на 2 разрядаPиY
P00 00 00 00 00 --- 11 10 10 10 00Y
5) y1y0 = 00, сдвиг на 2 разрядаPиY
P00 00 00 00 00 --- 00 11 10 10 10Y= 23410
