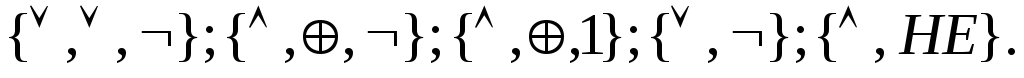- •Министерство образования и науки украины
- •Содержание
- •Глава 1 Арифметико-логические основы эвм
- •1.1 Информационные процессы
- •1.2. Обмен информацией между различными информационными устройствами
- •1.3. Аппаратные средства хранения и обработки информации
- •Глава 2 представление числовой информации в цифровом автомате
- •2.1. Системы счисления и понятие кода
- •2.2. Выбор системы счисления
- •2.3. Формальные правила двоичной арифметики
- •2.4. Перевод числа из одной позиционной системы счисления в другую
- •Глава 3 формы представления чисел в цифровых автоматах
- •3.1. Форма представления двоичных чисел с фиксированной запятой
- •3.2. Представление отрицательных чисел в формате с фиксированной запятой
- •3.3. Форма представление чисел с плавающей запятой
- •3.4. Перевод чисел из формата с фиксированной запятой в формат с плавающей запятой и обратно
- •3.5. Погрешности представления чисел
- •20 [A]ф2n- 1 для целых чисел
- •Глава 4. Арифметические действия с двоичными числами
- •4.1. Сложение двоичных чисел
- •4.1.1. Алгебраическое сложение чисел, представленных в форме с фиксированной запятой
- •4.1.2. Переполнение разрядной сетки
- •4.1.3. Модифицированный прямой, обратный и дополнительный код
- •4.1.4. Алгебраическое сложение чисел, представленных в форме с плавающей запятой
- •4.2. Умножение двоичных чисел
- •4.2.1. Методы умножения двоичных чисел
- •4.2.2. Умножение чисел, представленных в форме с фиксированной запятой
- •4.2.3. Умножение чисел, представленных в форме с плавающей запятой
- •4.2.4. Ускорение операции умножения
- •4.3. Деление двоичных чисел
- •4.3.1. Деление двоичных чисел, представленных в форме с фиксированной запятой.
- •4.3.2. Деление двоичных чисел, представленных в форме с плавающей запятой.
- •4.4. Оценка точности выполнения арифметических операций
- •4.4.1. Погрешность округления
- •Глава 5. Выполнение операций над двоично-десятичными числами
- •5.1. Представление десятичных чисел в д-кодах
- •5.2. Формальные правила поразрядного сложения в д-кодах
- •5.3. Представление отрицательных чисел в д-кодах
- •5.4. Выполнение операций сложения и вычитания в д-кодах
- •5.5. Умножение чисел в д-кодах
- •5.6. Деление чисел в д-кодах
- •5.7. Перевод чисел из д-кода в двоичный и из двоичного в д-код
- •Глава 6 Информационные основы цифровых автоматов
- •6.1. Понятие об информации и её преобразованиях
- •6.2. Преобразования алфавитной информации
- •6.3 Понятие об алгоритме
- •6.4 Понятие о дискретном (цифровом) автомате
- •Глава 7 Основы логического проектирования ца. Основные понятия алгебры логики.
- •7.1. Свойства элементарных функций алгебры логики
- •7.2. Аналитическое представление функций алгебры логики
- •7.3. Совершенные нормальные формы
- •7.4. Системы функций алгебры логики
- •7.5. Числовое и геометрическое представление фал
- •Глава 8 Минимизация функций алгебры логики
- •8.1 Метод Квайна
- •Ядро: мднф:
- •8.2 Метод Квайна-Мак-Класки
- •Простые импликанты: *111, 111*, 0**1
- •8.3 Метод Нельсона
- •8.4 Метод диаграмм Вейча
- •8.5 Метод самопонижающихся циклов
- •8.6 Минимизация монотонных функций
- •8.7 Минимизация конъюнктивных нормальных форм
- •8.8 Минимизация частично определенных булевых функций
- •8.9 Минимизация функций в базисах и-не и или-не
- •8.10 Минимизация систем булевых функций
- •Глава 9 Абстрактная теория автоматов
- •9.2 Декомпозиция абстрактных автоматов
- •Глава 10 Структурная теория автоматов
- •10.1 Композиция автоматов
- •Глава 11 Проектирование асинхронных цифровых автоматов
- •11.1 Проектирование комбинационных схем (кс) с учетом кобъед по входу и по выходу
- •11.2 Проектирование кс на дешифраторах и мультиплексорах
- •11.3 Проектирование кс на пзу
- •11.4 Проектирование кс на плм
- •Глава 12 Канонический метод структурного синтеза ца с памятью
- •12.1 Кодирование
- •12.2 Выбор элементов памяти автомата
- •12.3 Выбор структурно-полной системы элементов
- •12.4 Построение уравнений булевых функций возбуждения и выходов автомата
- •12.5 Построение функциональной схемы автомата
- •Глава 13 Обеспечение устойчивости функционирования ца
- •13.2 Проблема синтеза надёжных схем из ненадёжных элементов
- •13.3 Коды Хэмминга
- •Глава 14 Микропрограммные автоматы
- •14.2 Граф-схемы алгоритмов
7.2. Аналитическое представление функций алгебры логики
Существует много способов задания логических функций. Кроме табличного, используемого выше, при анализе ФАЛ используется аналитическая запись.
Рассмотрим
фиксированный набор переменных
![]() ,
на котором задана ФАЛ. Так как существует
переменная
,
на котором задана ФАЛ. Так как существует
переменная![]() ,
то набор значений переменных представляет
собой некоторое двоичное число. Пусть
номер набора будет двоичное число,
получаемое таким образом:
,
то набор значений переменных представляет
собой некоторое двоичное число. Пусть
номер набора будет двоичное число,
получаемое таким образом:![]()
Пусть
имеется функция
![]()
![]() -
называется термом.
-
называется термом.
Дизъюнктивный терм (макстерм) – это, связывающий все переменные знаком дизъюнкций (“конституэнта 0”).
Пример:
![]()
Конъюнктивный терм (минтерм) - это терм, связывающий все переменные знаком конъюнкции (“конституэнта 1”).
![]()
![]()
Ранг терма определяется количеством переменных, входящих в заданный терм.
Любая ФАЛ может быть представлена дизъюнкцией минтермов.
![]() –нормальная
дизъюнктивная форма (НДФ) – объединение
минтермов переменного ранга. В этой
форме вместо дизъюнкции может
использоваться
–нормальная
дизъюнктивная форма (НДФ) – объединение
минтермов переменного ранга. В этой
форме вместо дизъюнкции может
использоваться
![]() .
.
Любая ФАЛ может быть представлена конъюнкцией макстермов
![]() ,
где k
– количество двоичных наборов, для
которых. Такое представление называется
НКФ, знак конъюнкции может быть заменен
,
где k
– количество двоичных наборов, для
которых. Такое представление называется
НКФ, знак конъюнкции может быть заменен
![]() .
.
7.3. Совершенные нормальные формы
НКФ и НДФ не дают однозначного представления функции. Такое представление получается только при совершенных НФ.
СНДФ
– ФАЛ, заданная в виде:
![]() ,
где
,
где![]() и
и
![]() .
.
Основные свойства СНДФ:
В СНДФ нет двух одинаковых минтермов;
В СНДФ ни один минтерм не содержит двух одинаковых множителей (переменных);
В СНДФ ни один минтерм не содержит вместе с переменной и её отрицание.
Выписывать в СНДФ имеет смысл только конституэнты 1, соответствующие единичным наборам функции.
Любая
ФАЛ, кроме абсолютно истинной функции,
может быть представлена в СНДФ:
![]()
Пример: Функция задана таблицей истинности.
Представим ее в СНДФ и СНКФ.
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
СДНФ:
![]()
СКНФ:
![]()
Способы преобразования НФ в СНФ. СНФ отличается от НФ тем, что содержит термы максимального ранга и даёт однозначное представление функции.
Произвольная НДФ переводится в СДНФ таким образом:
Пусть
![]() ,
тогда
,
тогда![]() ,
где
,
где![]() – переменная, которая не входит в данный
терм.
– переменная, которая не входит в данный
терм.
Пример: Преобразовать ФАЛ в СДНФ:
![]()
Произвольная
НКФ переводится в СКНФ таким образом,
пусть
![]() ,
тогда
,
тогда
![]()
7.4. Системы функций алгебры логики
Любая булева функция может быть представлена одной из НФ. Эти формы используют ограниченное число элементарных булевых функций.
Например:
для СДНФ такие функции
![]() .
.
Следовательно, существуют системы ФАЛ с помощью которых можно аналитически представить любую сколь угодно сложную булеву функцию. Проектирование ЦА основано на знании таких систем ФАЛ из которых можно построить произвольный ЦА.
Базисом,
функционально полной системой булевых
функций (ФПСБФ) называют совокупность
таких булевых функций
![]() ,
что произвольная ФАЛ
,
что произвольная ФАЛ
![]() может быть записана в виде формулы через
функции этой совокупности.
может быть записана в виде формулы через
функции этой совокупности.
ФПСБФ:
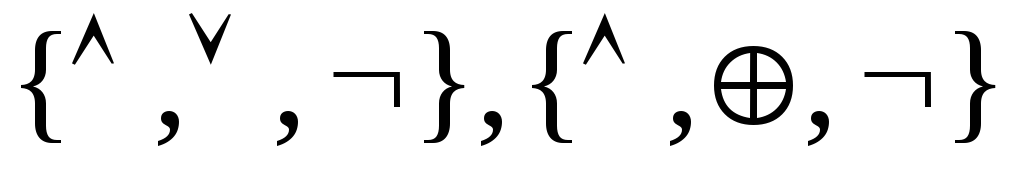
Определим свойства, которыми должна обладать функция, составляющие ФПСБФ. Рассмотрим предполные классы ФАЛ. Проведённые исследования показали, что предполных классов – 5, а для построения ФПСБФ необходимо и достаточно, чтобы её функции не содержались полностью ни в одном из 5 предполных классов.
Предполные классы ФАЛ:
класс функций, сохраняющих const 0
класс функций, сохраняющих const 1
класс самодвойственных булевых функций
класс линейных булевых функций
класс монотонных булевых функций
Функции
класса 2. Если функция на единичном
наборе = 1, то говорят, что она сохраняет
единицу
![]() .
.
Функция
класса 1. –
![]() .
.
Функции класса 3. ФАЛ называют самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения, то есть
![]()
Функции
класса 4. К линейным ФАЛ относятся
функции, которые могут представить в
виде
![]() ,
где
,
где![]() .
.
Функции класса 5. ФАЛ называют монотонной, если при любом возрастании набора значения этой функции не убывают.
Теорема Поста-Яблонского. Для того, чтобы система ФАЛ была функционально полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию:
не сохраняющую 0,
не сохраняющую 1,
не являющуюся линейной,
немонотонную,
не самодвойственную.
Рассмотрим примеры ФПСБФ:
|
|
Функция |
классы | |||||||
|
00 |
01 |
10 |
11 |
|
|
|
|
| |
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
|
+ |
+ |
+ |
+ |
+ |
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
+ |
+ |
+ |
+ |
+ |
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
Функции
![]() и
и![]() являются ФПСБФ. Из таблицы можно получить
и другие ФПСБФ:
являются ФПСБФ. Из таблицы можно получить
и другие ФПСБФ:![]()