
- •Министерство образования и науки украины
- •Содержание
- •Глава 1 Арифметико-логические основы эвм
- •1.1 Информационные процессы
- •1.2. Обмен информацией между различными информационными устройствами
- •1.3. Аппаратные средства хранения и обработки информации
- •Глава 2 представление числовой информации в цифровом автомате
- •2.1. Системы счисления и понятие кода
- •2.2. Выбор системы счисления
- •2.3. Формальные правила двоичной арифметики
- •2.4. Перевод числа из одной позиционной системы счисления в другую
- •Глава 3 формы представления чисел в цифровых автоматах
- •3.1. Форма представления двоичных чисел с фиксированной запятой
- •3.2. Представление отрицательных чисел в формате с фиксированной запятой
- •3.3. Форма представление чисел с плавающей запятой
- •3.4. Перевод чисел из формата с фиксированной запятой в формат с плавающей запятой и обратно
- •3.5. Погрешности представления чисел
- •20 [A]ф2n- 1 для целых чисел
- •Глава 4. Арифметические действия с двоичными числами
- •4.1. Сложение двоичных чисел
- •4.1.1. Алгебраическое сложение чисел, представленных в форме с фиксированной запятой
- •4.1.2. Переполнение разрядной сетки
- •4.1.3. Модифицированный прямой, обратный и дополнительный код
- •4.1.4. Алгебраическое сложение чисел, представленных в форме с плавающей запятой
- •4.2. Умножение двоичных чисел
- •4.2.1. Методы умножения двоичных чисел
- •4.2.2. Умножение чисел, представленных в форме с фиксированной запятой
- •4.2.3. Умножение чисел, представленных в форме с плавающей запятой
- •4.2.4. Ускорение операции умножения
- •4.3. Деление двоичных чисел
- •4.3.1. Деление двоичных чисел, представленных в форме с фиксированной запятой.
- •4.3.2. Деление двоичных чисел, представленных в форме с плавающей запятой.
- •4.4. Оценка точности выполнения арифметических операций
- •4.4.1. Погрешность округления
- •Глава 5. Выполнение операций над двоично-десятичными числами
- •5.1. Представление десятичных чисел в д-кодах
- •5.2. Формальные правила поразрядного сложения в д-кодах
- •5.3. Представление отрицательных чисел в д-кодах
- •5.4. Выполнение операций сложения и вычитания в д-кодах
- •5.5. Умножение чисел в д-кодах
- •5.6. Деление чисел в д-кодах
- •5.7. Перевод чисел из д-кода в двоичный и из двоичного в д-код
- •Глава 6 Информационные основы цифровых автоматов
- •6.1. Понятие об информации и её преобразованиях
- •6.2. Преобразования алфавитной информации
- •6.3 Понятие об алгоритме
- •6.4 Понятие о дискретном (цифровом) автомате
- •Глава 7 Основы логического проектирования ца. Основные понятия алгебры логики.
- •7.1. Свойства элементарных функций алгебры логики
- •7.2. Аналитическое представление функций алгебры логики
- •7.3. Совершенные нормальные формы
- •7.4. Системы функций алгебры логики
- •7.5. Числовое и геометрическое представление фал
- •Глава 8 Минимизация функций алгебры логики
- •8.1 Метод Квайна
- •Ядро: мднф:
- •8.2 Метод Квайна-Мак-Класки
- •Простые импликанты: *111, 111*, 0**1
- •8.3 Метод Нельсона
- •8.4 Метод диаграмм Вейча
- •8.5 Метод самопонижающихся циклов
- •8.6 Минимизация монотонных функций
- •8.7 Минимизация конъюнктивных нормальных форм
- •8.8 Минимизация частично определенных булевых функций
- •8.9 Минимизация функций в базисах и-не и или-не
- •8.10 Минимизация систем булевых функций
- •Глава 9 Абстрактная теория автоматов
- •9.2 Декомпозиция абстрактных автоматов
- •Глава 10 Структурная теория автоматов
- •10.1 Композиция автоматов
- •Глава 11 Проектирование асинхронных цифровых автоматов
- •11.1 Проектирование комбинационных схем (кс) с учетом кобъед по входу и по выходу
- •11.2 Проектирование кс на дешифраторах и мультиплексорах
- •11.3 Проектирование кс на пзу
- •11.4 Проектирование кс на плм
- •Глава 12 Канонический метод структурного синтеза ца с памятью
- •12.1 Кодирование
- •12.2 Выбор элементов памяти автомата
- •12.3 Выбор структурно-полной системы элементов
- •12.4 Построение уравнений булевых функций возбуждения и выходов автомата
- •12.5 Построение функциональной схемы автомата
- •Глава 13 Обеспечение устойчивости функционирования ца
- •13.2 Проблема синтеза надёжных схем из ненадёжных элементов
- •13.3 Коды Хэмминга
- •Глава 14 Микропрограммные автоматы
- •14.2 Граф-схемы алгоритмов
7.5. Числовое и геометрическое представление фал
Часто
для упрощения записи ФАЛ вместо полного
перечисления термов используют номера
наборов, для которых функция = 1. Например
![]() ,
то есть на 0, 3 и 4-м наборах функция = 1.
Такая форма записи называется числовой.
,
то есть на 0, 3 и 4-м наборах функция = 1.
Такая форма записи называется числовой.
Ф АЛ
имеют и геометрическое представление,
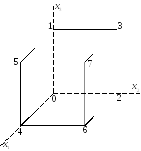
так функция 2-х переменных рассматривают
как плоскость, заданную в системе
координат
АЛ
имеют и геометрическое представление,
так функция 2-х переменных рассматривают
как плоскость, заданную в системе
координат![]() .
Отложим по каждой оси единичные отрезки
.
Отложим по каждой оси единичные отрезки![]() и
и![]() .
Получим квадрат, вершины которого –
комбинации переменных.
.
Получим квадрат, вершины которого –
комбинации переменных.
Две вершины, принадлежащие одному ребру “склеиваются” по переменной меняющейся вдоль ребра.
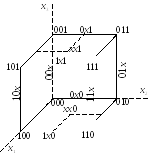
Для
функции 3-х переменных геометрическое
представление выполняются в виде куба,
вершины которого обозначены десятичными
цифрами, двоичными цифрами и произвольными
переменными
![]() .
Рёбра куба поглощают вершины. Грани
куба поглощают свои рёбра и, следовательно,
вершины.
.
Рёбра куба поглощают вершины. Грани
куба поглощают свои рёбра и, следовательно,
вершины.
Терм
максимального ранга называют 0-кубом
(точкой) и обозначают
![]() .
.
Пусть
![]()

Если
два 0-куба из
![]() различаются только по одной координате,
то они образуют 1-куб (отрезок):
различаются только по одной координате,
то они образуют 1-куб (отрезок):![]() ,
где х – независимая координата.
,
где х – независимая координата.
Если два 1-куба различны только по одной координате, то они образуют 2-куб (грань).
Трёхмерный куб получается при соединении соответствующих вершин двух двумерных кубов отрезками единичной длины.
Глава 8 Минимизация функций алгебры логики
Общая задача минимизации булевых функций может быть сформулирована таким образом: найти аналитическое выражение заданной булевой функции в форме, содержащей минимальное число букв. Эта задача достаточно хорошо исследована в классе дизъюнктивно – конъюнктивных форм.
Определение: Минимальной ДНФ булевой функции называется ДНФ, содержащая наименьшее число букв по отношению к другим ДНФ, представляющим заданную булеву функцию.
Определение: Булева функция q(x1… xn)
называется импликантой булевой
функции f(x1… xn)
если для любого набора переменных,
на котором![]() ,
справедливо
,
справедливо![]() .
.
Определение: Импликанта
![]() булевой функции
булевой функции![]() ,
являющаяся элементарной конъюнкцией,
называется простой, если никакая часть
импликанты
,
являющаяся элементарной конъюнкцией,
называется простой, если никакая часть
импликанты![]() не является импликантой функции
не является импликантой функции![]() .
.
Дизъюнкция любого числа импликант булевой функции
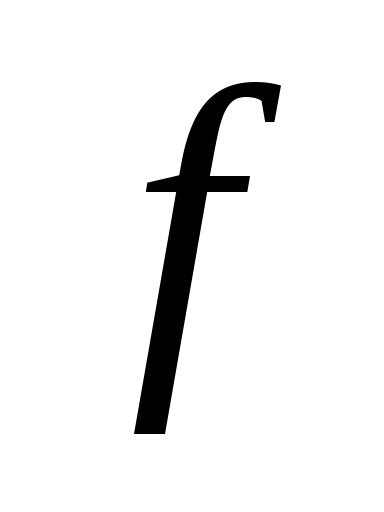 так же является импликантой этой
функции.
так же является импликантой этой
функции.Любая булева функция
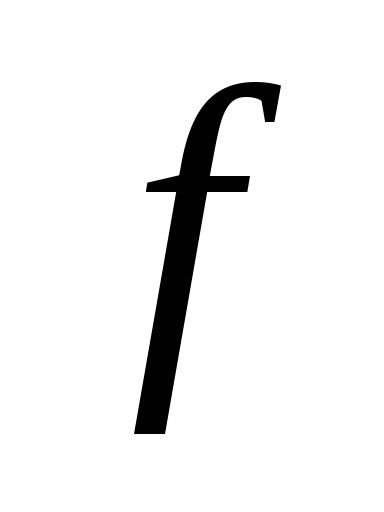 эквивалентна дизъюнкции всех своих
простых импликант. Такая форма называется
сокращенной ДНФ.
эквивалентна дизъюнкции всех своих
простых импликант. Такая форма называется
сокращенной ДНФ.
Пример:
|
x1 |
x2 |
x3 |
f |
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
q7 |
|
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 0 0 1 0 0 1 1 |
0 0 0 0 0 0 0 1 |
0 0 0 0 0 0 1 0 |
0 0 0 0 0 0 1 1 |
0 0 0 1 0 0 0 0 |
0 0 0 1 0 0 0 1 |
0 0 0 1 0 0 1 0 |
0 0 0 1 0 0 1 1 |
![]()

![]() и
и
![]() простые
импликанты.
простые
импликанты.
Сокращенная ДНФ
![]() :
:
Импликанты
![]() и
и
![]() покрывают своими "1" все "1"
функции
покрывают своими "1" все "1"
функции![]() .
.
Получение сокращенной ДНФ является первым этапом отыскания минимальных форм булевых функций. Иногда из СкДНФ можно убрать одну или несколько простых импликант, не нарушая эквивалентности исходной функции. Такие простые импликанты называются лишними. Их исключение из СкДНФ – второй этап минимизации.
Определение: СкДНФ булевой функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.
Тупиковые ДНФ булевых функций
![]() ,
содержащие минимальное число букв,
являются минимальными. МДНФ может быть
несколько.
,
содержащие минимальное число букв,
являются минимальными. МДНФ может быть
несколько.
