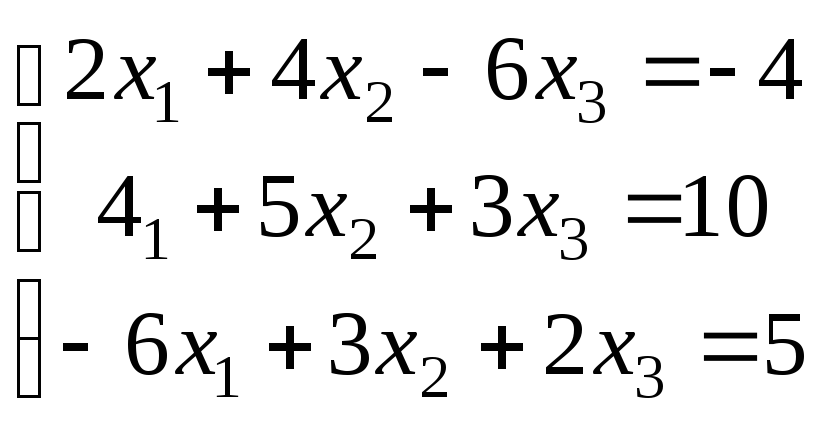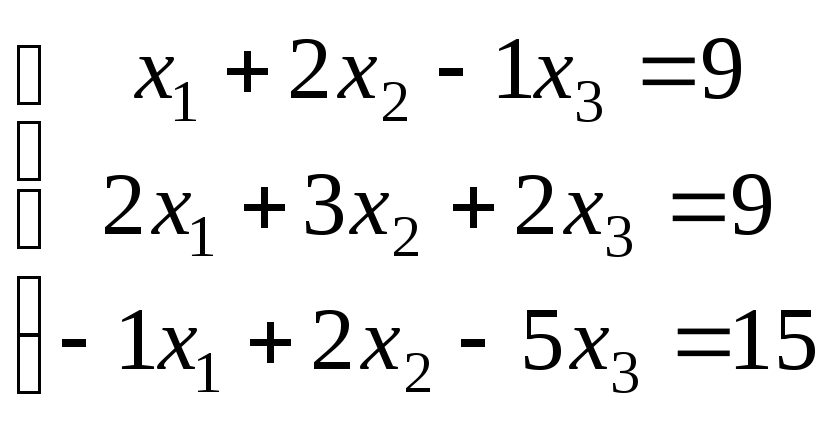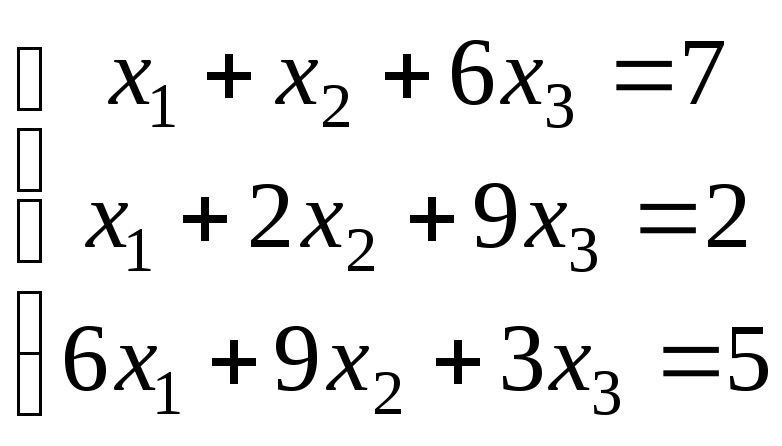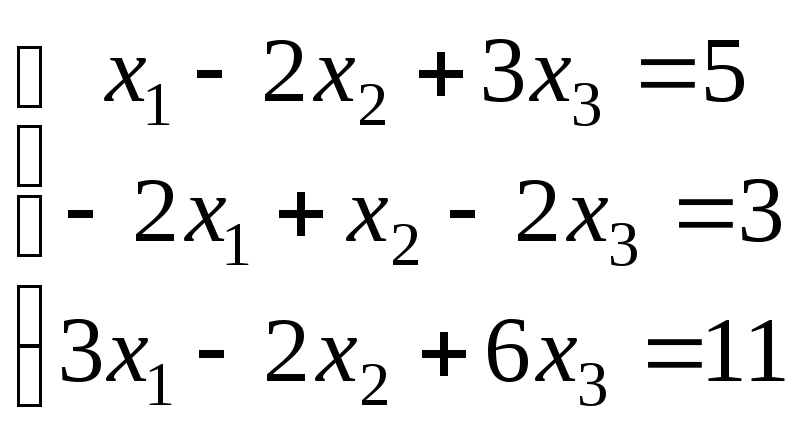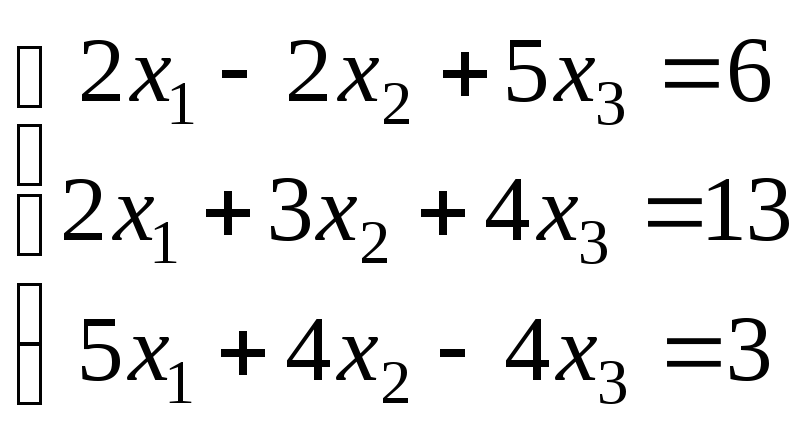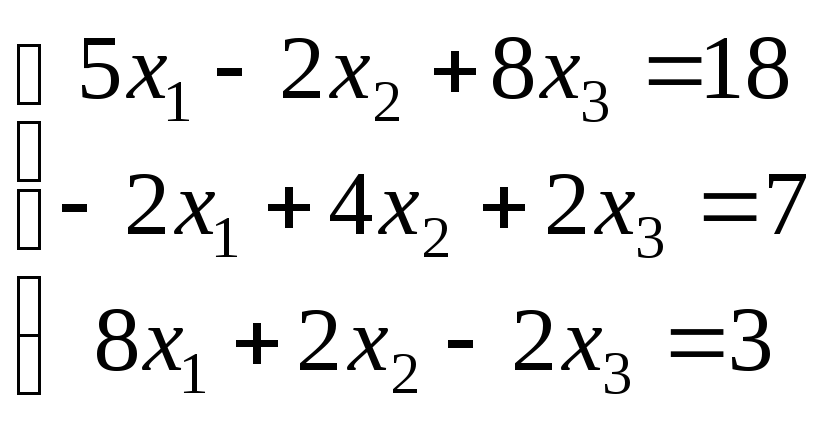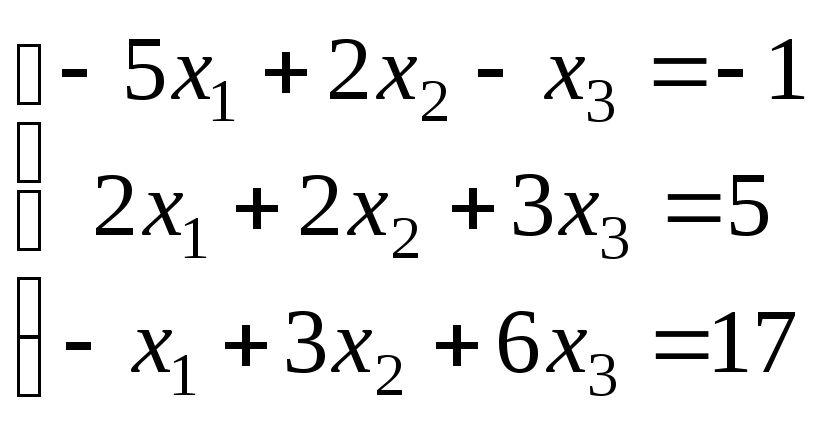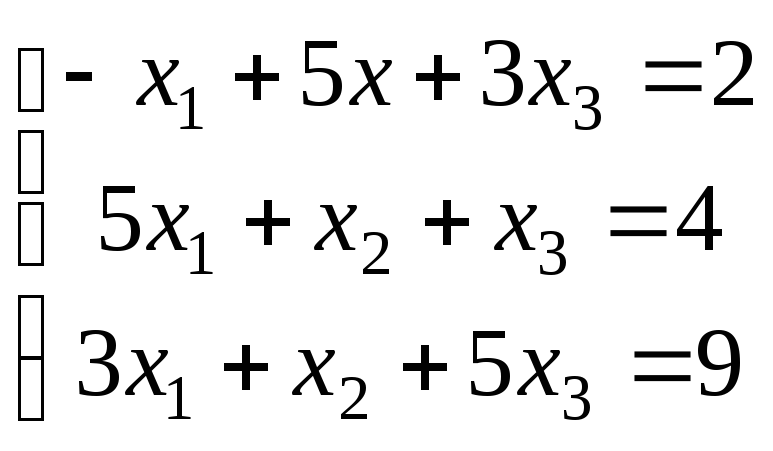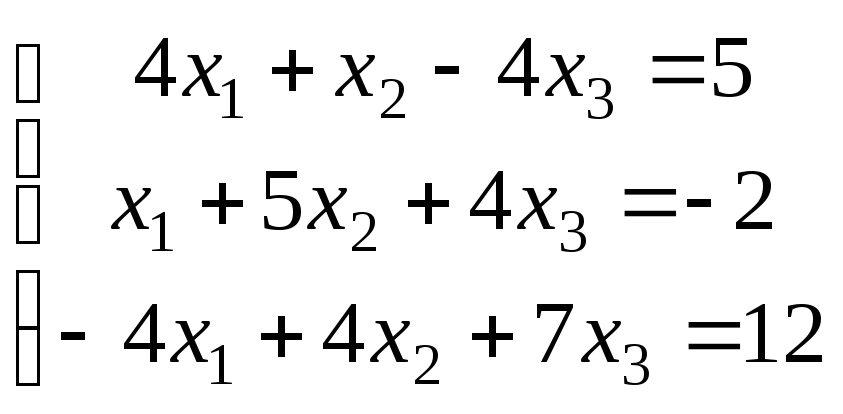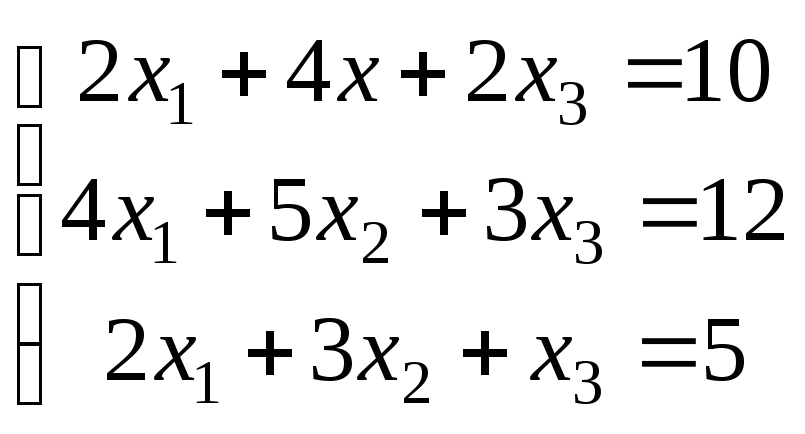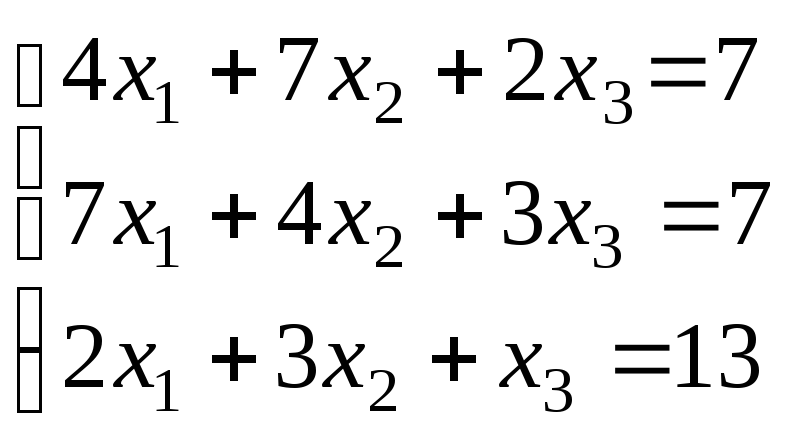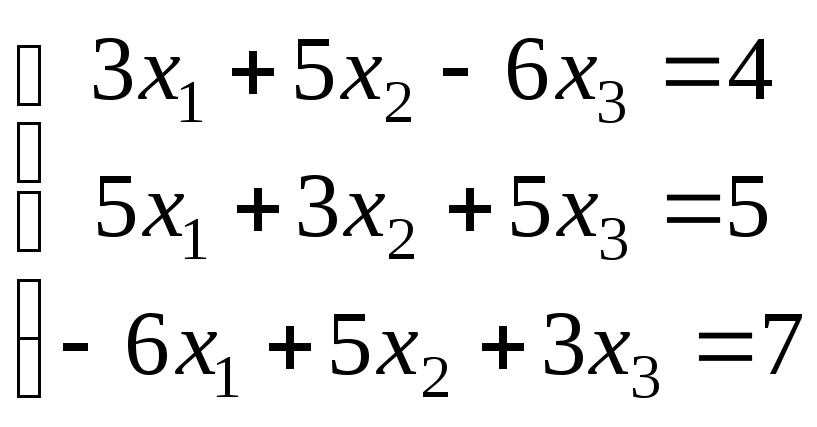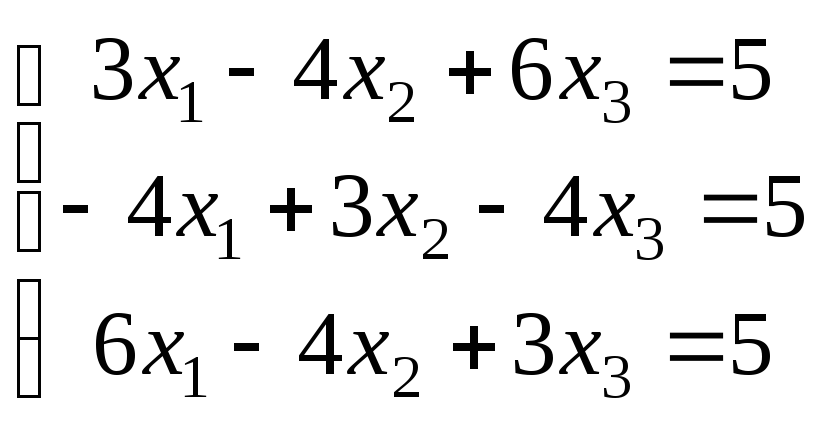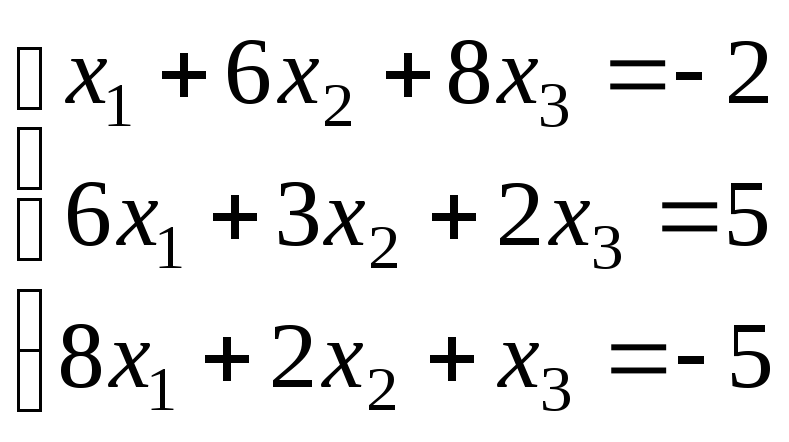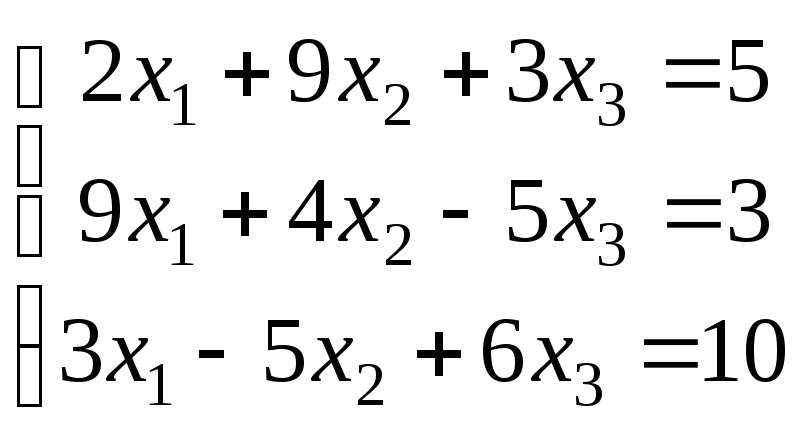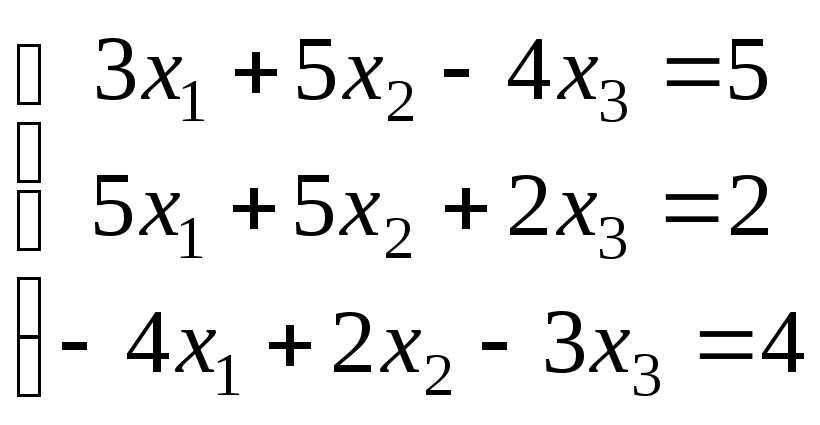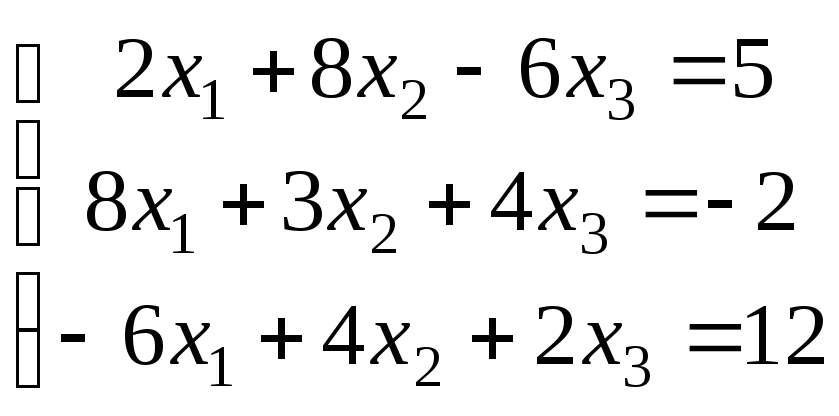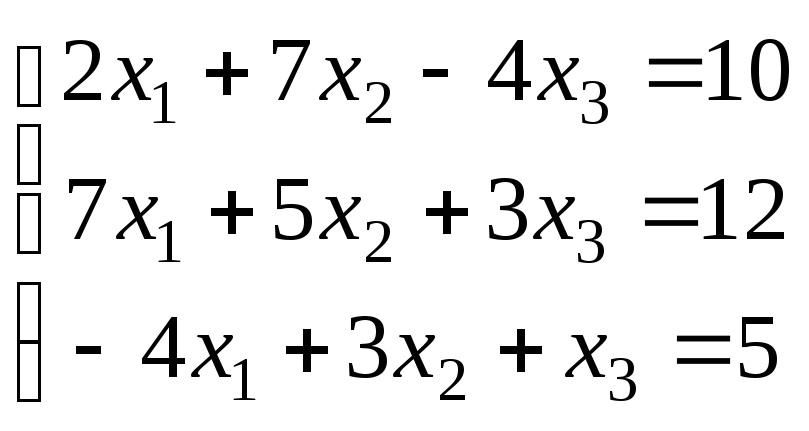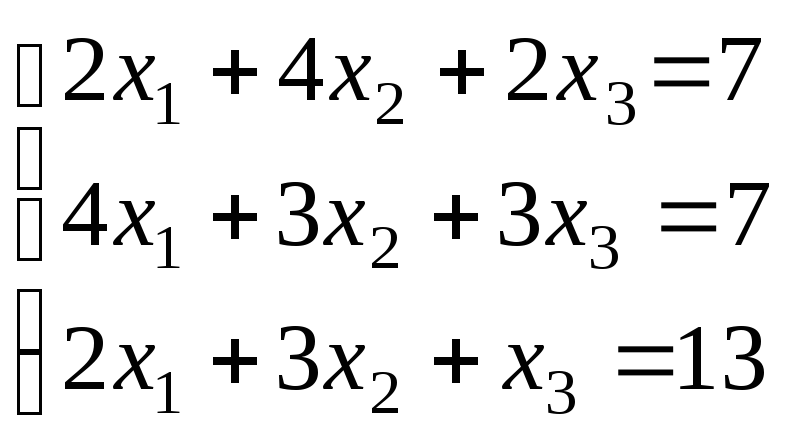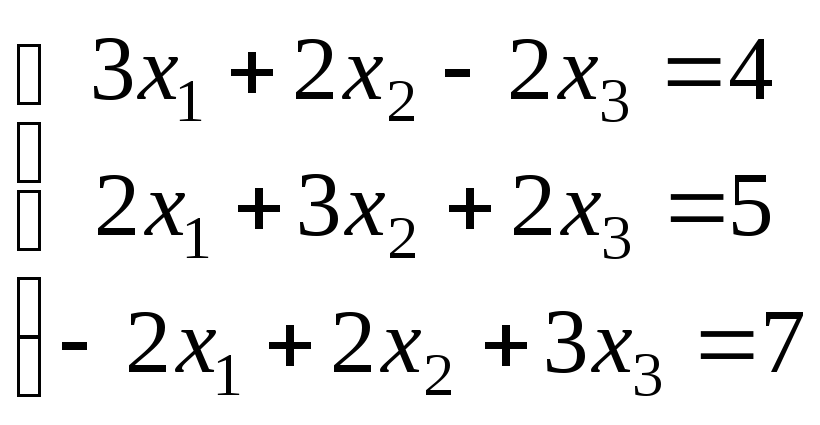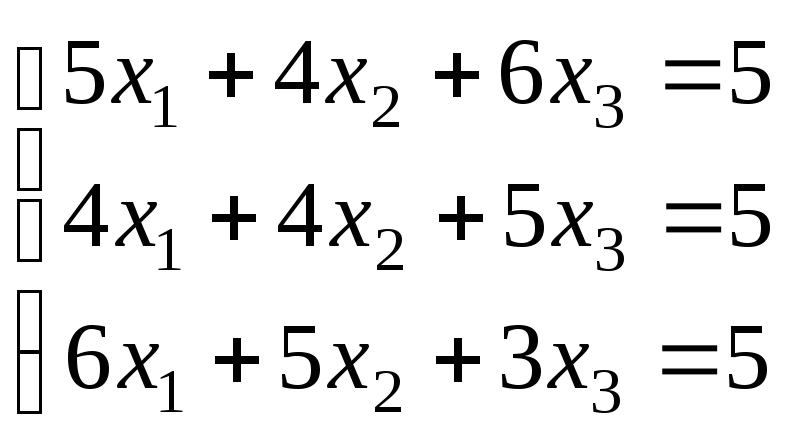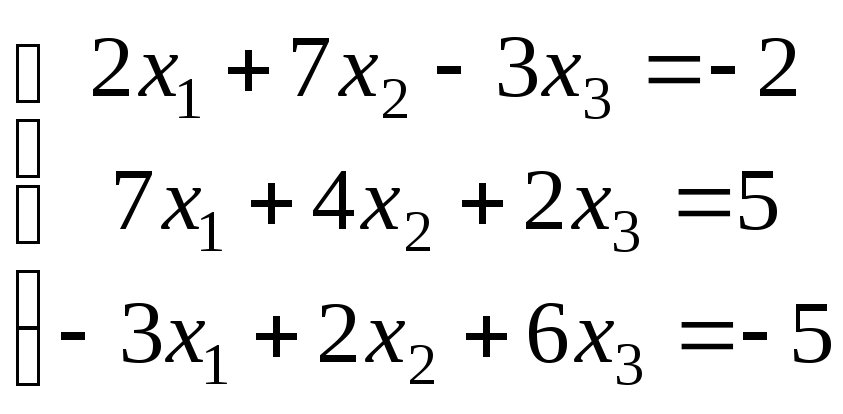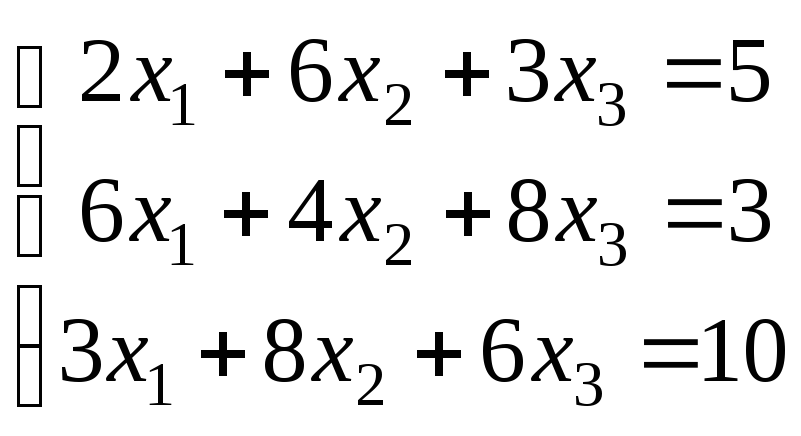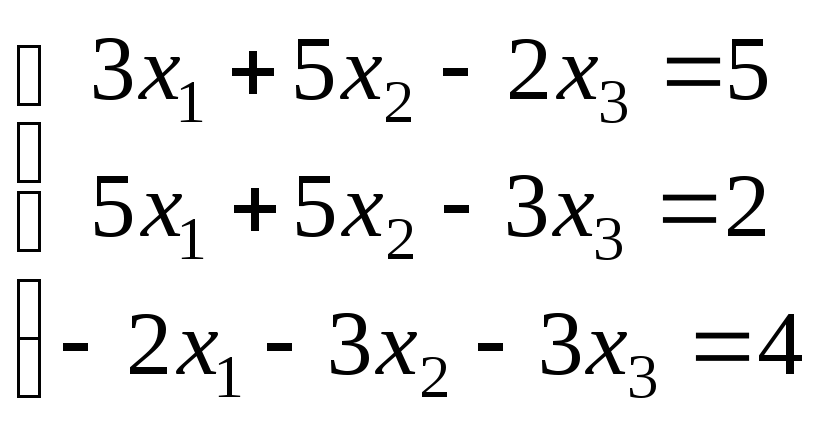- •Посібник з інформатики і системології
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця
- •1.1. Теоретична частина
- •1.2. Завдання для виконання лабораторної роботи
- •1.3 Приклад виконання роботи
- •1. Друкування та форматування тексту
- •2. Складання списків та їх форматування Кондитерська фабрика
- •3.Створення таблиці
- •4. Користування об’єктами WordArt
- •5. Створення формул
- •6. Складання блок-схеми
- •Питання для самоконтролю
- •Тема 2. Використання табличного процесора ms Excel в практичній роботі фахівця
- •2.1. Теоретична частина
- •2.2. Типи даних ет Excel
- •2.3. Сортування та фільтрація даних
- •2.4. Статистична обробка експериментальних даних на еп Excel (Завдання №1)
- •2.5. Завдання для виконання роботи
- •2.6. Приклад виконання роботи
- •2.7. Питання для самоконтролю
- •Тема 3. Алгоритмізація фахових задач та їх програмування на мові Pascal for Windows
- •3.1. Алгоритми
- •Фігури блок-схем
- •А) б)
- •3.2. Основи програмування на мові Pascal for Windows
- •3.3. Завдання для виконання лабораторної роботи
- •Завдання по темі
- •3.5. Питання для самоконтролю
- •Тема 4. Використання системи MathCad для розв’язування фахових задач
- •4.1. Загальні положення
- •4.2. Основи роботи в MathCad
- •1. Визначення змінних та їх результатів
- •4.3. Графічні об’єкти
- •В. Графічний вигляд функції
- •4.4. Символьний режим роботи
- •4.5. Завдання до виконання лабораторних робіт
- •Варіанти завдань
- •Варіанти до завдання 1
- •Варіанти до завдання 2
- •Варіанти до завдання 3
- •Варіанти завдання 4
- •Варіанти до завдання 5
- •4.6. Питання для самоконтролю
- •Тема 5. Розв’язування систем лінійних алгебраїчних рівнянь
- •5.1. Завдання до виконання роботи
- •Варіанти завдань
- •5.2. Питання для самоконтролю
- •Тема 6. Розв’язок нелінійних рівнянь та їх систем
- •6.1. Загальні положення
- •6.2. Етапи відокремлення коренів
- •6.3. Способи уточнення коренів
- •6.3.1. Метод половинного ділення (дихотомії)
- •6.3.2. Уточнення коренів методом хорд
- •6.3.3. Уточнення кореня методом дотичних (Ньютона)
- •6.3.4. Ітераційний метод уточнення кореня
- •6.3.5. Система нелінійних рівнянь
- •Варіанти завдань
- •6.4. Питання для самоконтролю
- •Тема 7. Інтерполяція і апроксимація функцій заданих таблично
- •7.1. Постановка задачі
- •7.2. Інтерполяційний поліном Лагранжа
- •7.3. Табличний метод застосування полінома Лагранжа
- •7.4. Інтерполяційні формули Ньютона
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •7.5. Обернена інтерполяція
- •Обернена інтерполяція
- •7.6. Апроксимація функцій методом найменших квадратів
- •7.7. Нелінійна апроксимація
- •Експоненціальна апроксимація
- •Варіанти завдань
- •7.9. Питання для самоконтролю
- •Тема 8. Чисельне диференціювання та інтегрування функцій
- •8.1. Наближене диференціювання
- •Диференціювання функції на базі
- •Варіанти завдань
- •8.3. Питання для самоконтролю
- •Тема 9: Чисельне інтегрування звичайних диференційних рівнянь
- •9.1. Загальні поняття
- •9.2. Метод Ейлера
- •9.3. Метод Рунге-Кутта
- •9.4. Інтегрування диференційних рівнянь інструментарієм системи MathCad
- •Функції rkfixed, Bulstoer таRkadapt
- •9.5. Завдання до виконання роботи
- •Варіанти завдань
- •9.6. Питання для самоконтролю
- •Тема 10. Чисельні методи оптимізації
- •10.1. Постановка задачі
- •10.2. Постановка задачі лінійного програмування
- •10.3. Геометрична інтерпретація злп
- •Графічний розв’язок злп
- •10.4. Симплекс-метод розв’язку злп
- •10.5. Розв’язок злп з допомогою ms Excel
- •Варіанти завдань
- •10.6. Транспортна задача
- •10.6.1. Постановка задачі
- •10.6.2. Метод північно-західного кута
- •Варіанти транспортної задачі
- •10.7. Питання для самоконтролю
- •Тема 11. Власні значення та власні вектори
- •11.1. Загальні поняття
- •11.2. Власні значення
- •11.3 Власні вектори
- •11.4 Знаходження найбільшого власного числа
- •11.5 Завдання
- •Варіанти завдань
- •11.6 Питання для самоперевірки
- •Література
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця 4
11.3 Власні вектори
Кожному
значенню
![]() відповідає нескінченна множина однаково
направлених, але різної довжини власних
векторів. Всі вони можуть бути визначені
із матричного рівняння
відповідає нескінченна множина однаково
направлених, але різної довжини власних
векторів. Всі вони можуть бути визначені
із матричного рівняння![]() .
.
Щоб виділити із множини таких векторів один з них, необхідно для нього задати одну із координат.
Для
розглянутого прикладу при
![]() маємо:
маємо:
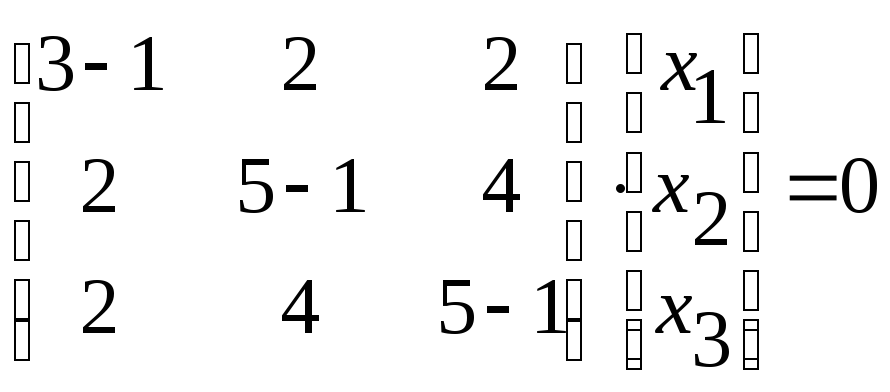 .
.
Задамося
![]() і розділимо досліджуване матричне
рівняння на субматриці:
і розділимо досліджуване матричне
рівняння на субматриці:
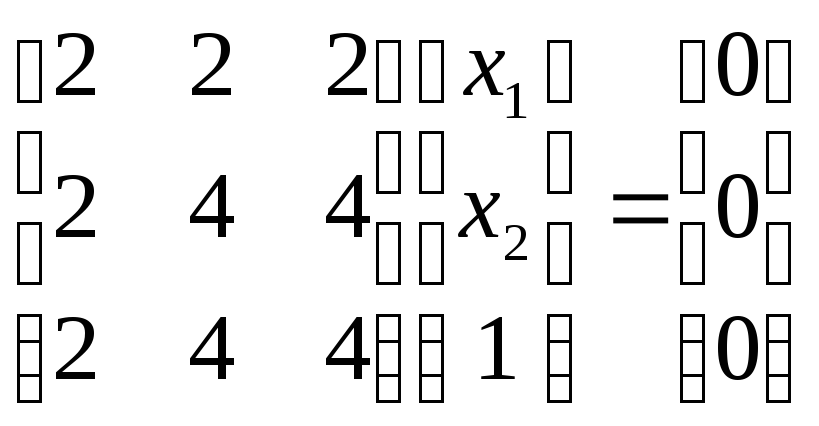



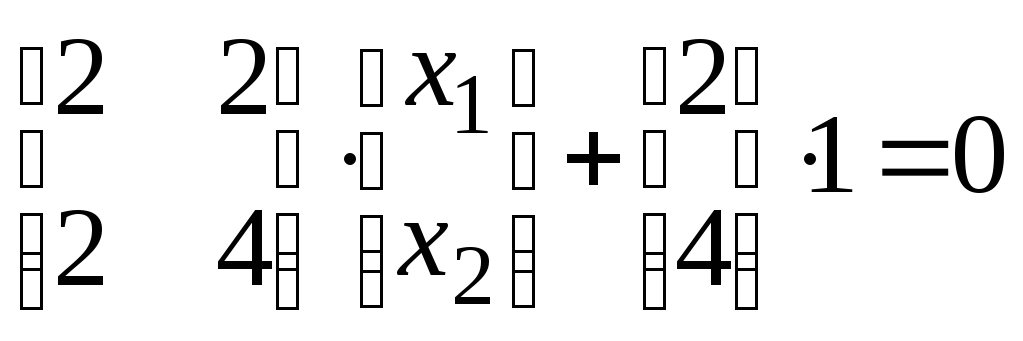
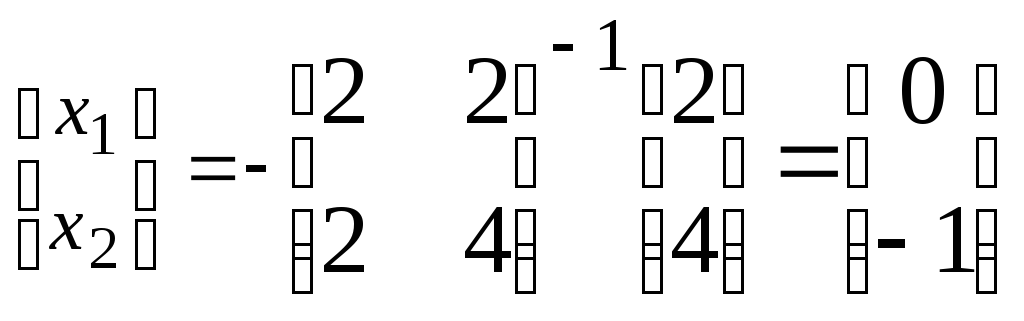 .
.
Отже,
власний вектор, що відповідає власному
значенню
![]() має координати
має координати
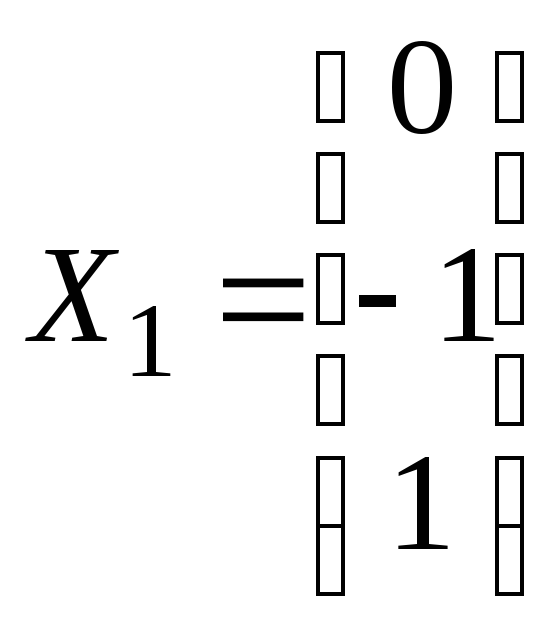 .
.
Перевіримо:
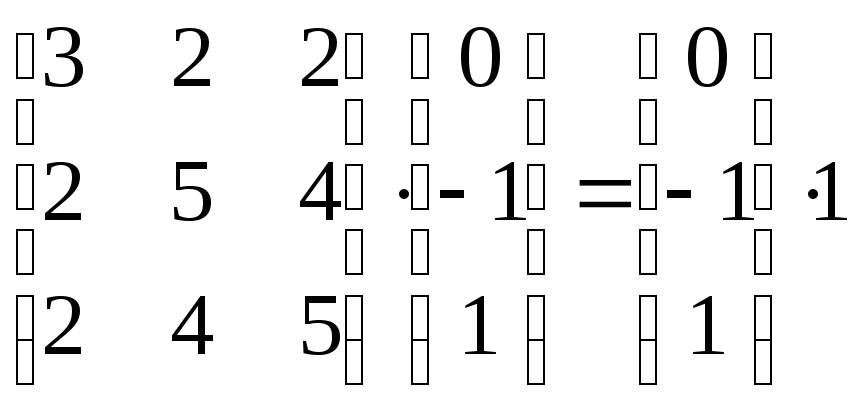 .
.
Для
![]() маємо рівняння:
маємо рівняння:
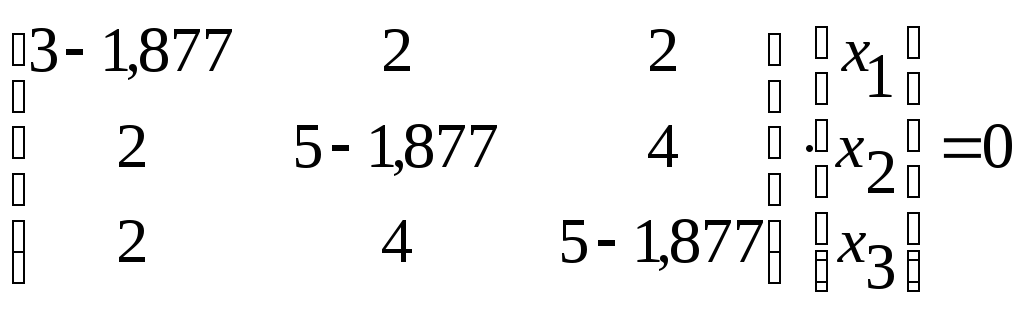 .
.
Задаючи
![]() ,
маємо:
,
маємо:
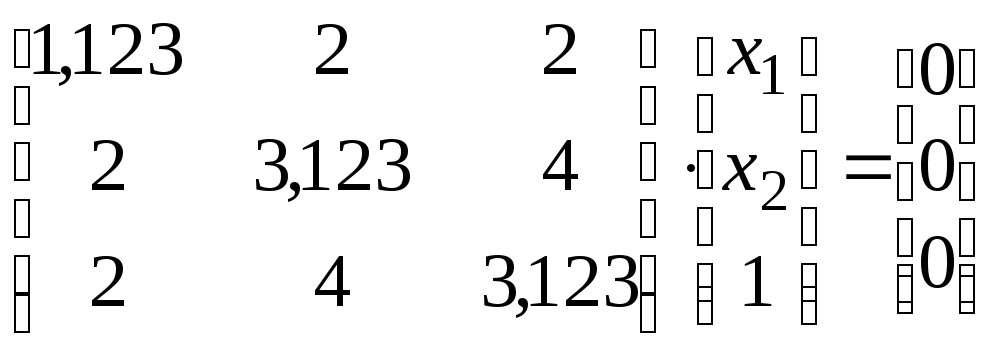


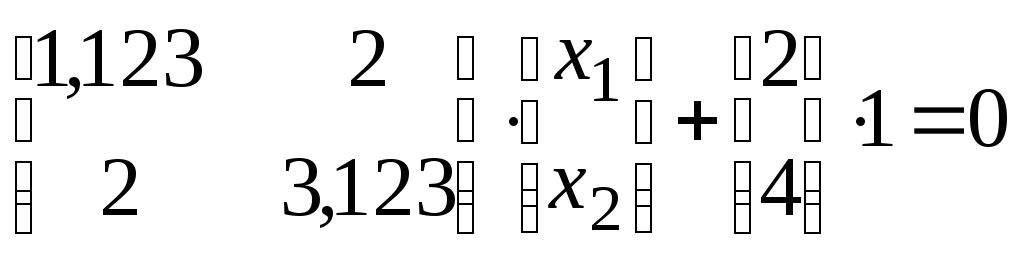
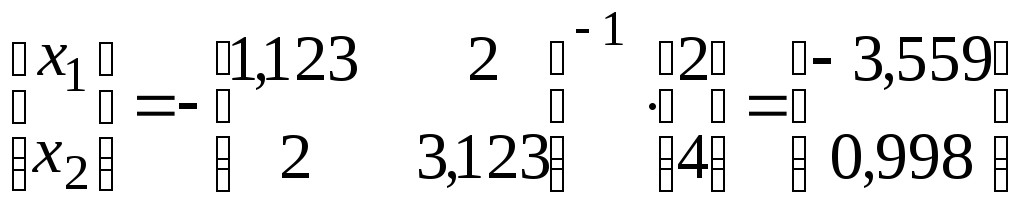 .
.
Отже, другий власний вектор має координати
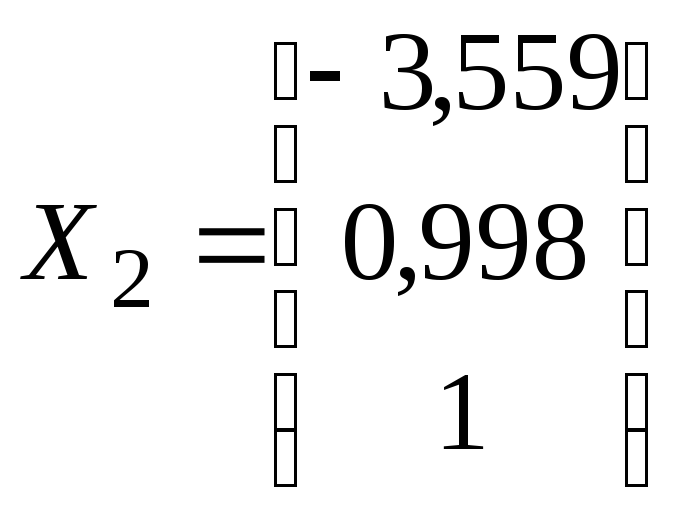 .
.
Перевіряємо:
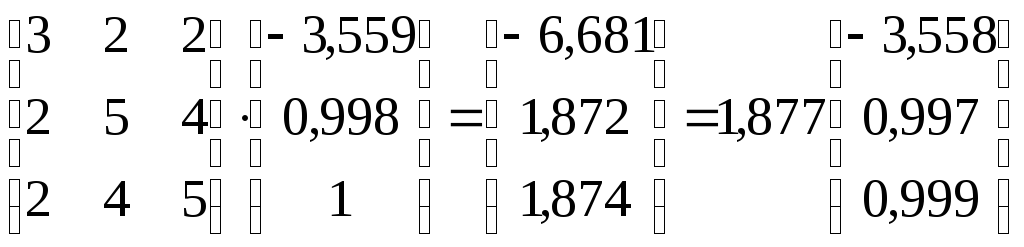 .
.
Для
![]() одержуємо аналогічним способом третій
власний вектор матриціА:
одержуємо аналогічним способом третій
власний вектор матриціА:
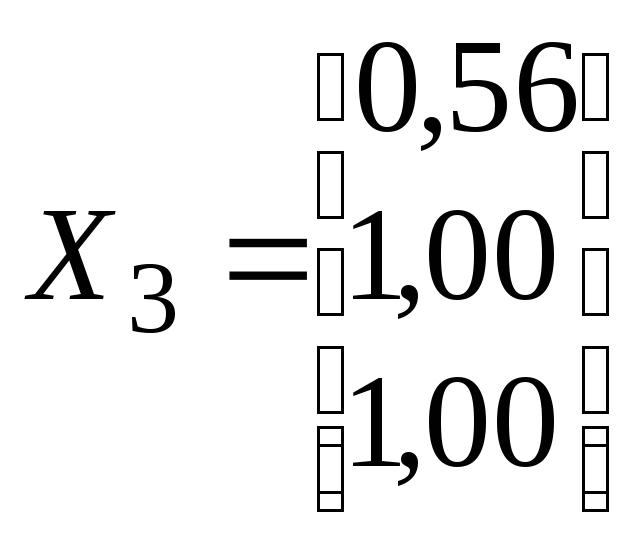
Перевіряємо:
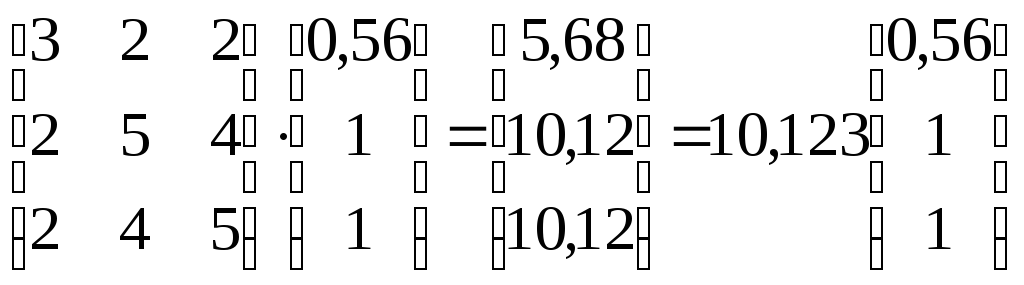 .
.
Невелика розбіжність в третьому знаці результату з’явилася за рахунок роботи з неточними числами.
11.4 Знаходження найбільшого власного числа
При
аналізі технічних систем часто досить
знати не всі власні значення і відповідні
до них власні вектори, а лише деякі з
них. Наприклад, в задачі про коливання
балки найбільший практичний інтерес
становить перша частота коливань, а в
задачі про напружений стан у точці
деформованого пружного тіла бажано
знати лише значення найбільшого головного
напруження, яке відповідає найбільшому
власному значенню напружень
![]() .
В такій постановці мова йде про часткову
проблему власних значень. Для її
розв’язання ефективними є ітераційні
методи.
.
В такій постановці мова йде про часткову
проблему власних значень. Для її
розв’язання ефективними є ітераційні
методи.
Ітераційний
процес відшукання найбільшого власного
значення
![]() випливає із системи рівнянь:
випливає із системи рівнянь:
![]() (11.1)
(11.1)
Якщо
декілька разів повторити операцію
множення АХ,
то результуючий вектор буде збільшуватись
в основному за рахунок найбільшого по
модулю
![]() .
Якщо на деякій ітерації взяти відношення
відображеного вектора до попереднього,
то це і буде наближене значення
.
Якщо на деякій ітерації взяти відношення
відображеного вектора до попереднього,
то це і буде наближене значення![]() .
.
Застосуємо
цей метод для одержання
![]() попереднього прикладу. Візьмемо за
первісний вектор
попереднього прикладу. Візьмемо за
первісний вектор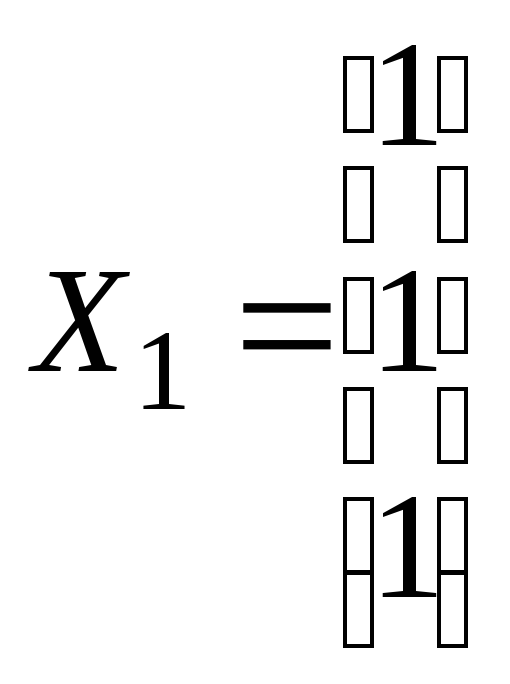 .
.
1.
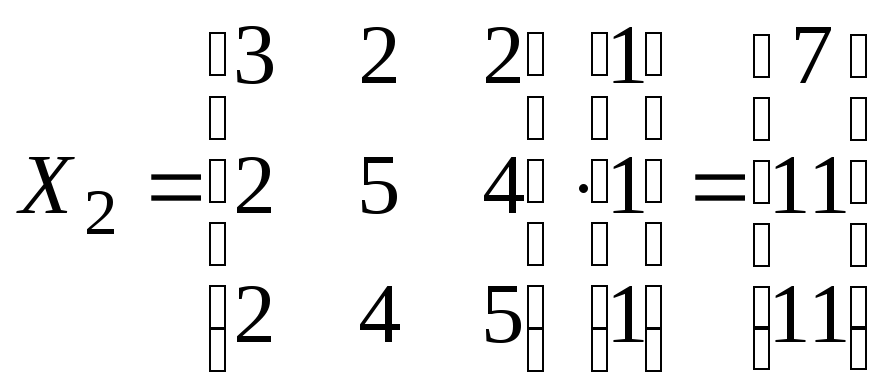 .
.
2.
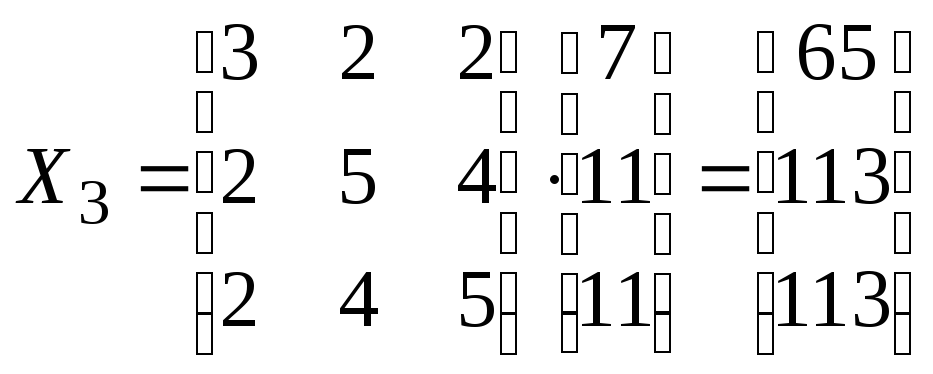
![]() .
.
3.
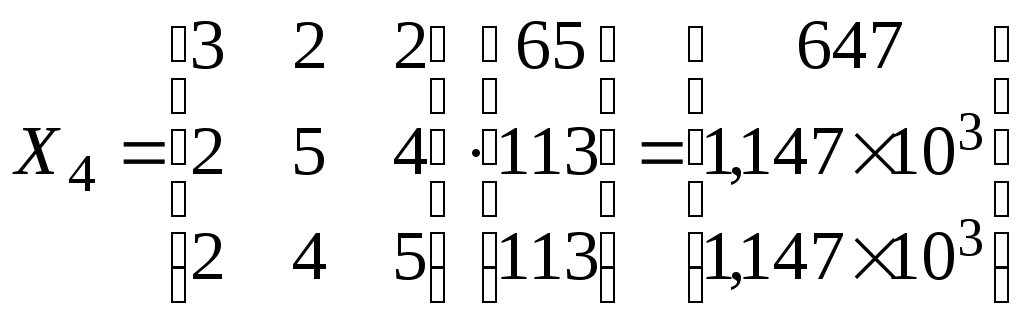
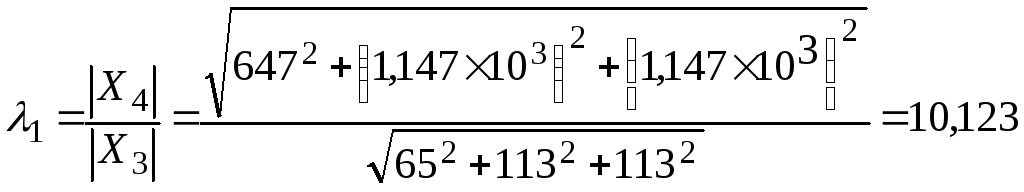 .
.
Тобто
уже на третій ітерації, з точністю три
знаки після коми, ми одержали найбільше
власне значення матриці. Така швидка
збіжність пояснюється тим, що
![]() в нашому прикладі значно більша за
в нашому прикладі значно більша за![]() та
та![]() .
.
Для
одержання найменшого власного значення
матричний вираз (11.1) помножимо зліва на
![]() :
:
![]()
звідки
![]() .
.
Тобто маємо такий же ітераційний процес, але з оберненою матрицею А.
11.5 Завдання
В
таблиці вибрати варіанти матриці А,
одержати для неї та для її матриці
власні числа та власні вектори. Впевнитися,
що модулі матриці
мають величину меншу за 1. Для матриці
А
знайти
![]() та
та![]() .
.
Варіанти завдань
|
Варіант |
Система рівнянь |
Варіант |
Система рівнянь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад виконання .

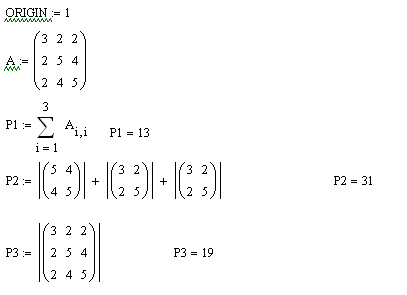

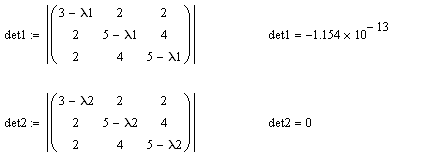
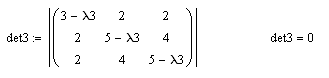


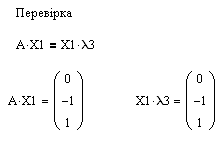

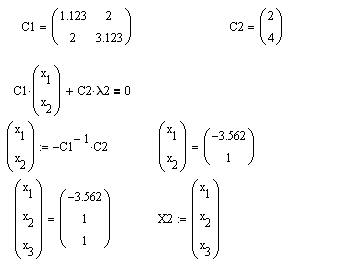
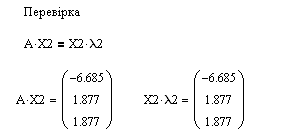



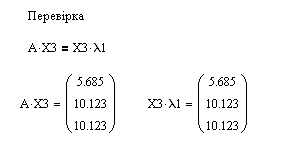



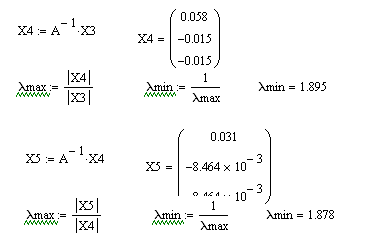




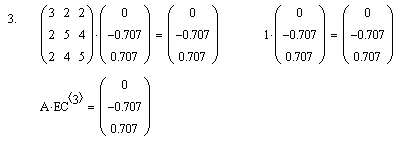
11.6 Питання для самоперевірки
Які вектори називаються власними векторами?
Що таке головна вісь матриці?
Що таке власне значення матриці?
За якої умови можна знайти власні значення матриці?
Що таке визначник матриці?
Як обчислити визначник матриці 3-го порядку?
Що називається віковим визначником?
Як отримати характеристичне рівняння n-го степеню?
Що ми отримаємо після розкриття вікового визначника n-го степеню?
Як обрахувати слід матриці
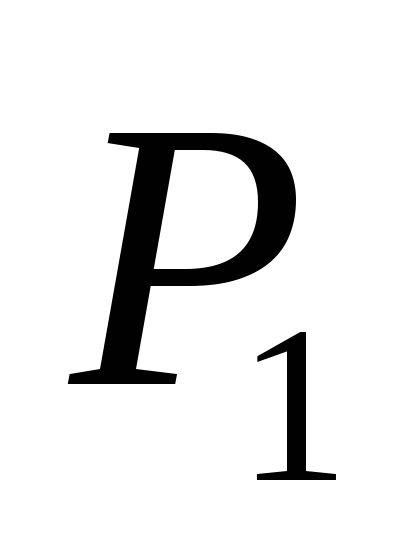 ?
?За якою формулою можна знайти суму діагональних мінорів другого порядку?
За якою формулою можна знайти суму діагональних мінорів третього порядку?
Якщо розмірність матриці більше трьох, то яким чином отримують мінори?
Як розв’язати характеристичне рівняння за допомогою символьного процесора MathCad?
В яких фахових задачах застосовується знаходження найбільших або найменших власних значень?
Із якої системи рівнянь випливає ітераційний процес знаходження найбільшого власного значення?
Як знайти найменше власне значення?
Яка функція в MathCad обчислює вектор, елементами якого є власні значення матриці А?
Яка функція в MathCad обчислює матрицю, яка містить нормовані вектори, які відповідають власним значенням матриці А?
Яка функція в MathCad обчислює власний вектор для матриці А і заданого власного значення l?