9.2. Метод Ейлера

Цей метод являється відносно наближеним і застосовується в основному для орієнтовних розрахунків. Однак ідея метода являється основоположною в цілий ряд більш точних методів.

Зміст методу полягає в тому, що в точцірозглядається, як крива, визначена через її похідну. Початкові умовидозволять вибирати із множини кривих єдину, що проходить через точку. В цій точці проведемо дотичнуі рухаємось по ній на деяку відстань(крок інтегрування) і приходимо в точку.

Значення функції в цій точці (рисунок 33)

.

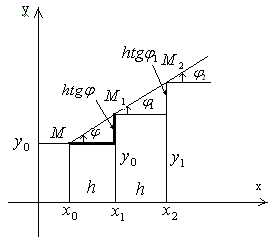
Рисунок 33 – Геометрична інтерпретація метода Ейлера

Продовжуючи цю процедуру далі одержуємо послідовність коротких відрізків і т.д., які з достатнім наближенням задають шукану функцію. Таким чином, ітераційна формула метода Ейлера має вигляд. Точність такого методу пропорційна кроку інтегрування. Тобто, щоб збільшити точність результату на одну значущу цифру, потрібно крок інтегрування збільшити в 10 разів.

9.3. Метод Рунге-Кутта

Існує багато більш точних, ніж метод Ейлера, методів інтегрування звичайних диференційних рівнянь (Адамса, Ейлера-Коші, Мільса та ін.). Але всі вони основані на визначенні кута нахилу дотичних до шуканої кривої в різних точках кроку інтегрування. Найбільш точним методом вважають метод Рунге-Кутта IV порядку.

Так же як і в методі Ейлера значення шуканої функції визначають за формулою .

Якщо розкласти в ряд Тейлора і обмежитися членами довключно, то приріст функціїможна представити у вигляді:

(9.1)

Замість безпосередніх обчислень по формулі (9.1) визначаються 4 числа:

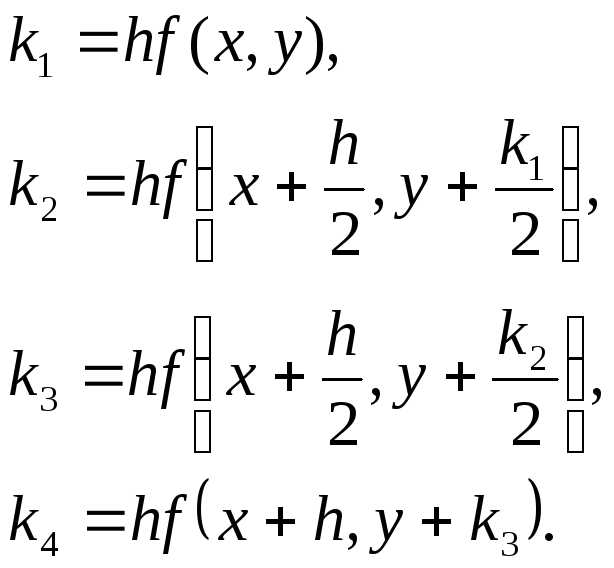(9.2)

Як видно із значень цих коефіцієнтів, вони відповідають приросту функції на початку кроку інтегрування, в кінці кроку та в двох точках між ними. А тому середнє значення таких приростів знаходять за формулою:

.

Таким чином, для кожної пари поточних значень ,маємо ітераційні перетворення:

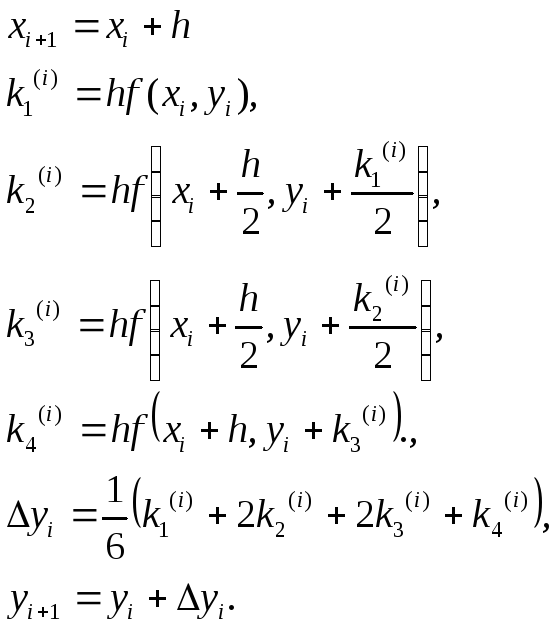
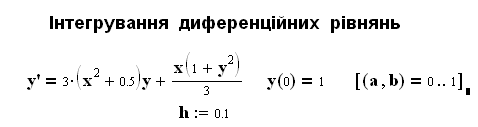
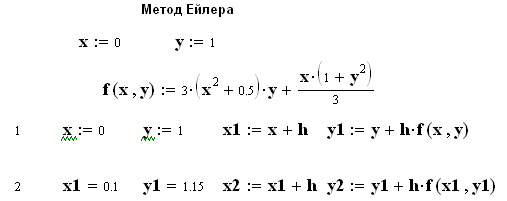
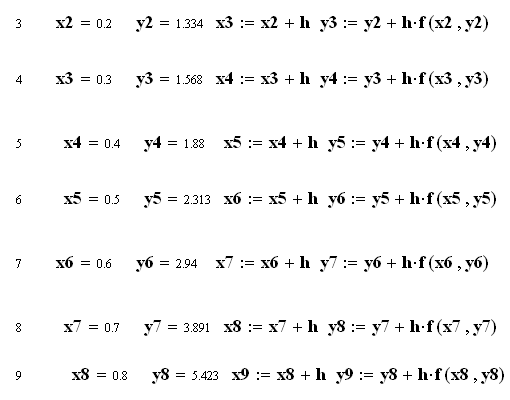
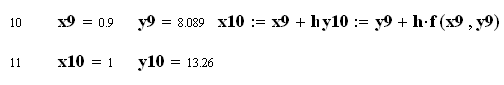
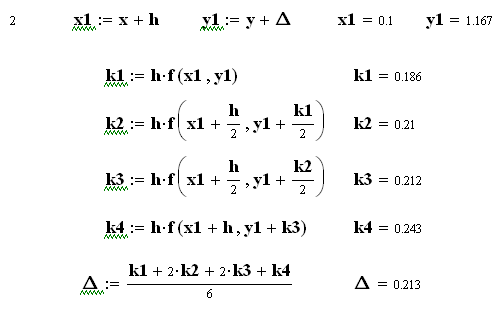
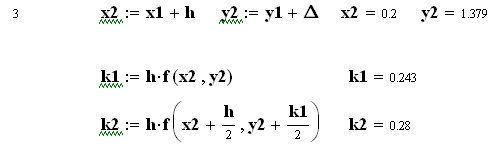
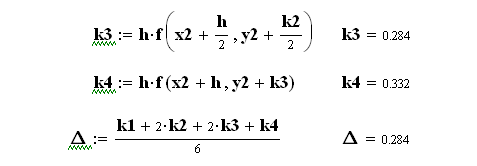
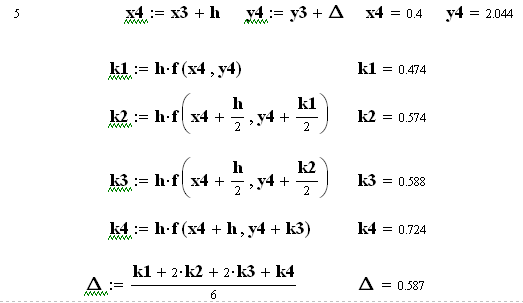
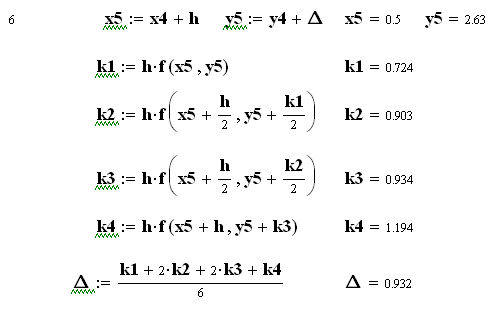
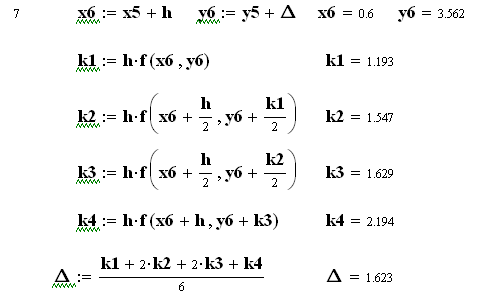
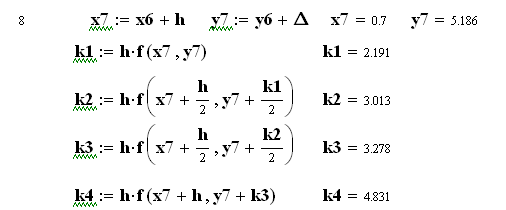
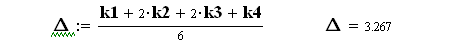
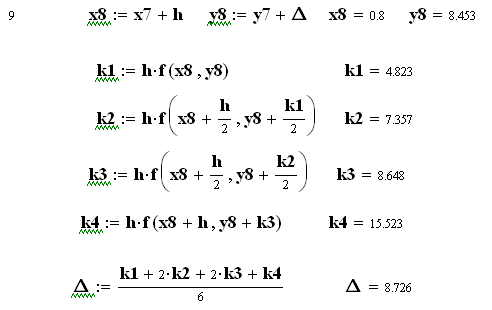
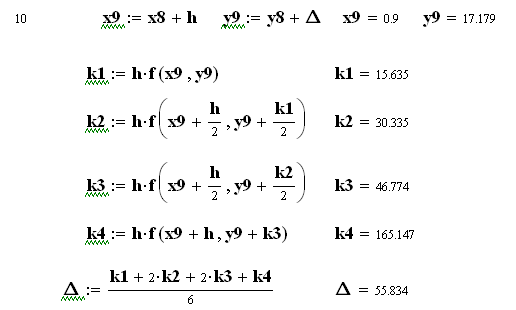
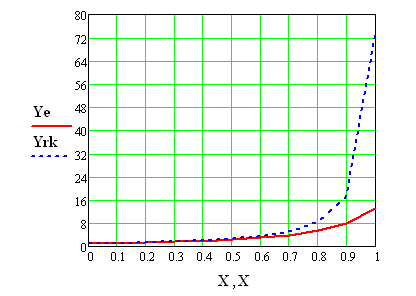
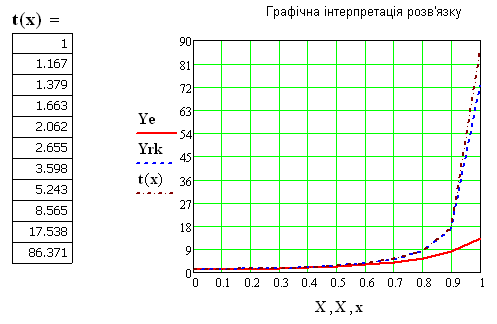
Як бачимо, на початку діапазону інтегрування результати методів практично співпадають, а далі похибка методу Ейлера суттєво збільшується.

9.4. Інтегрування диференційних рівнянь інструментарієм системи MathCad

Для розв’язку диференційних рівнянь в системі MathCad є цілий ряд вмонтованих функцій. Розглянемо можливість застосування деяких з них.

9.4.1. Функція odesolve(x,b,n),

де х – аргумент шуканої функції ;

b – кінець інтервалу інтегрування;

n – число кроків інтегрування.

Технологія застосування цієї функції має таку послідовність:

• ввести службове слово Given;

• ввести диференційне рівняння в вигляді:

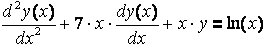
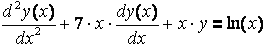
або

або

(для занесення апострофа потрібно натиснути +).

• ввести початкові умови: .

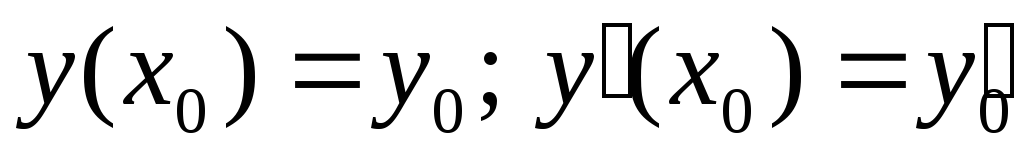• записати функцію: .

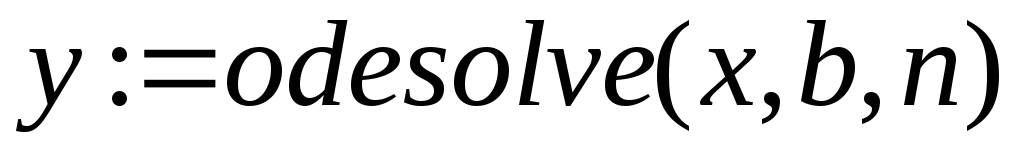Розв’язок буде знаходитися в пам’яті комп’ютера. Щоб його вивести, потрібно:

• присвоїти змінній х значення потрібного діапазону .

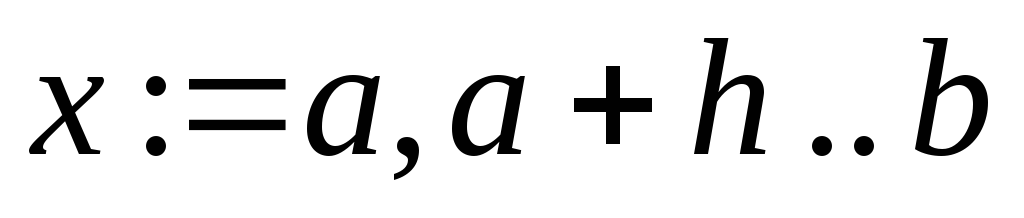• ввести ім’я функції та натиснути клавішу .

На робоче поле буде виведена в табличному вигляді шукана функція .

9.4.2. Вмонтовані функції: rkfixed, Bulstoer, Rkadapt.

Ці функції мають однакові параметри:

,

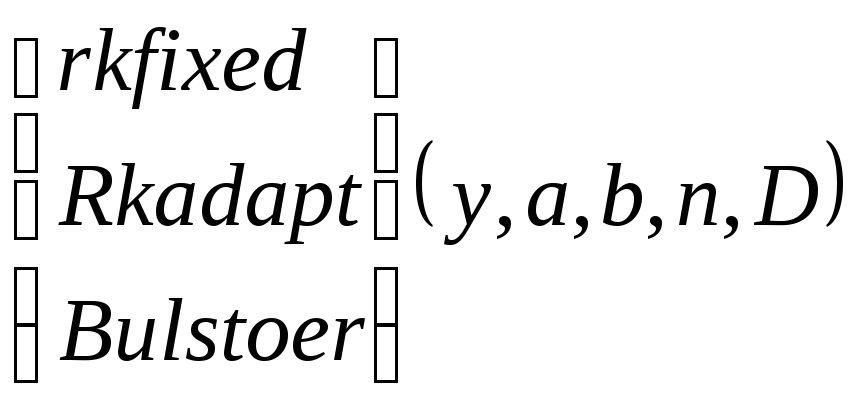де y – вектор початкових умов;

a, b – діапазон інтегрування;

n – кількість кроків розв’язку;

D – вектор правих частин системи диференційних рівнянь.

Технологія розв’язку системи дифрівнянь така:

• ввести вектор початкових умов з присвоєнням йому імені y (або всяке інше); якщо це єдине рівняння у присвоюється скаляр;

• ввести вектор правих частин системи: ;

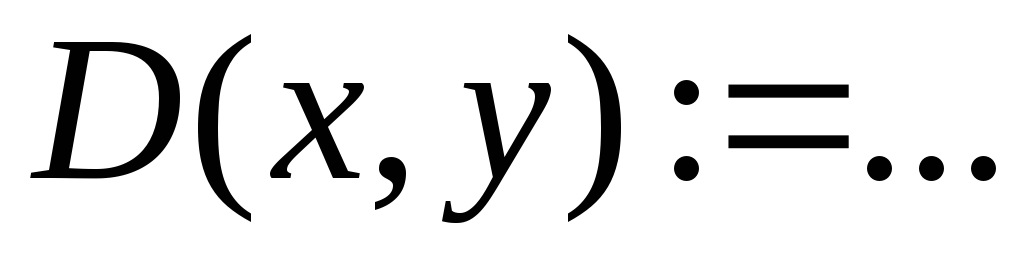• присвоїти ідентифікатор функції: .

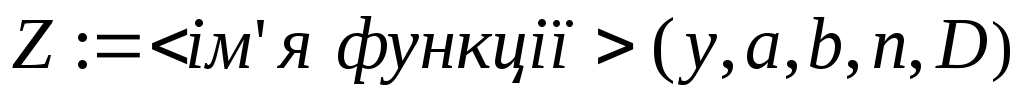Для виведення результату на екран: і друкується таблиця, в нульовому стовпці якої роздруковано значеннях, а в першому . Для представлення їх на графіку потрібно задати кількість точок аргументуі розмістити його в нижньому маркері графіка, а вертикальному маркері задається перший стовпчик таблиці.

Розв’язок диференційних рівнянь інструментарієм MathCad