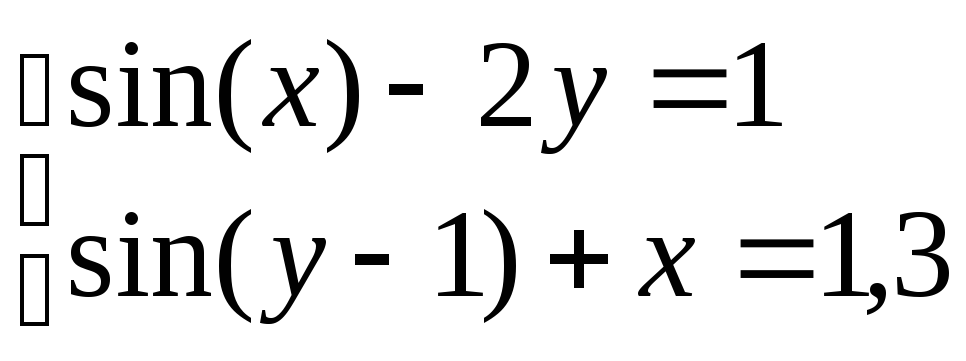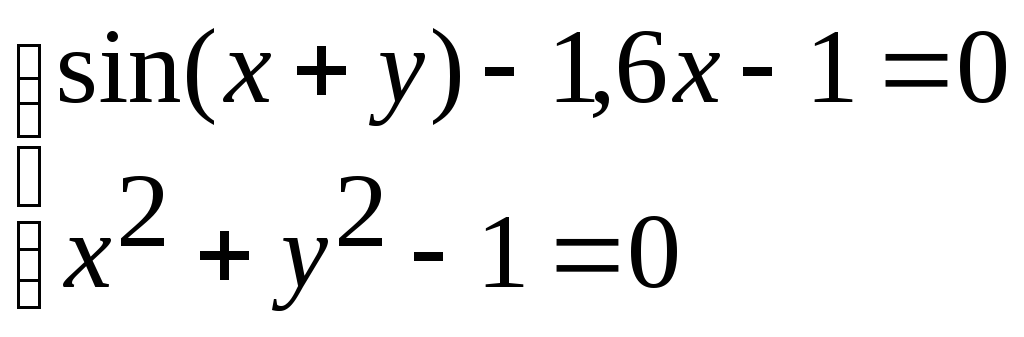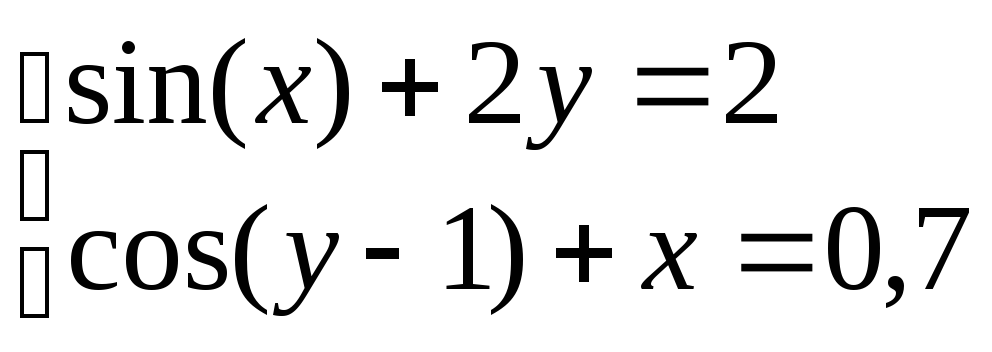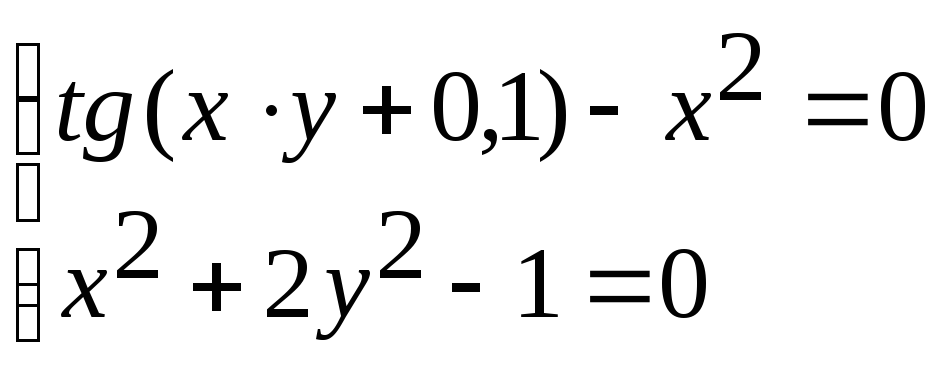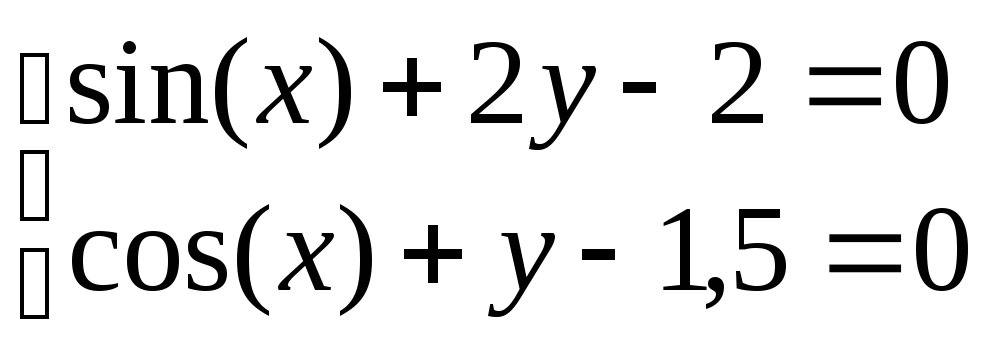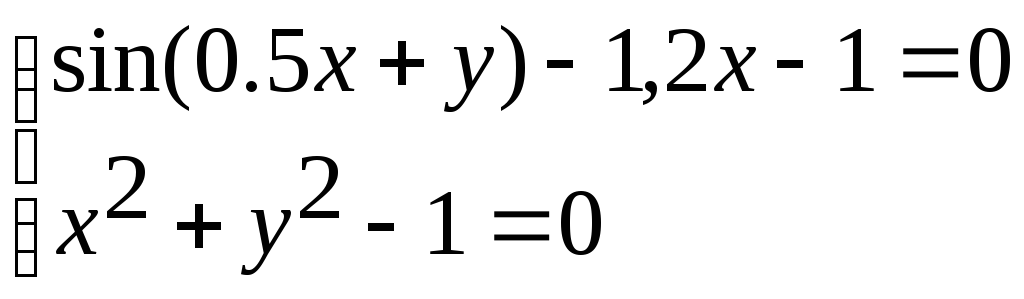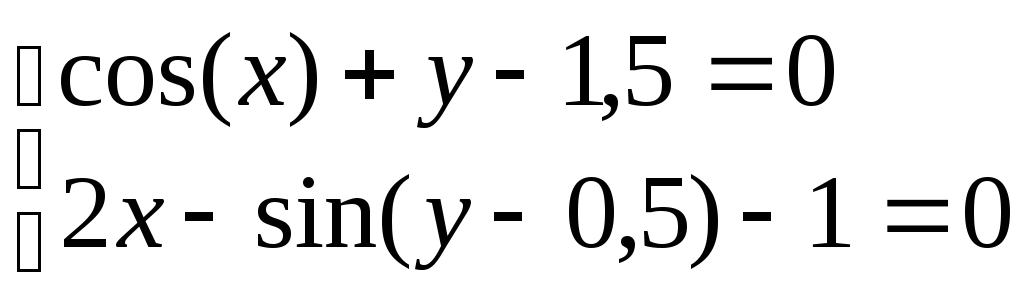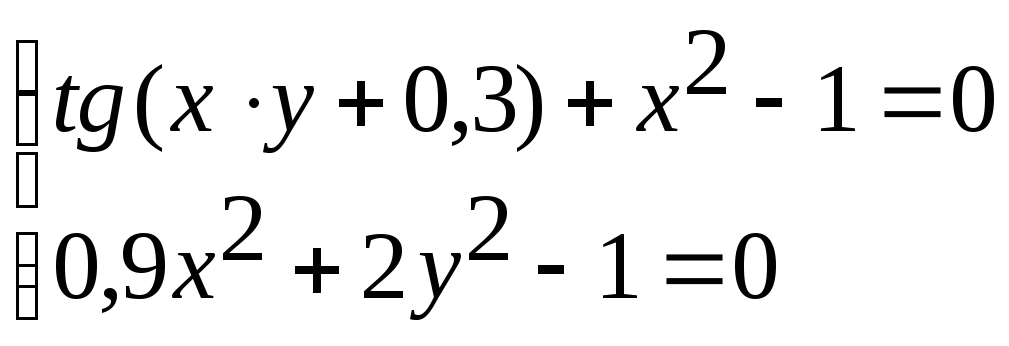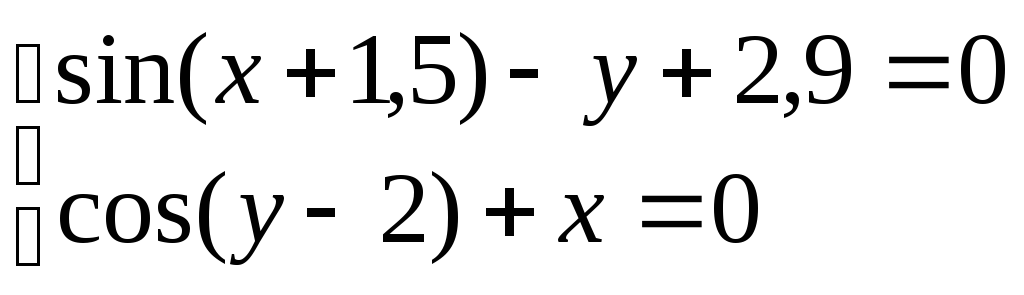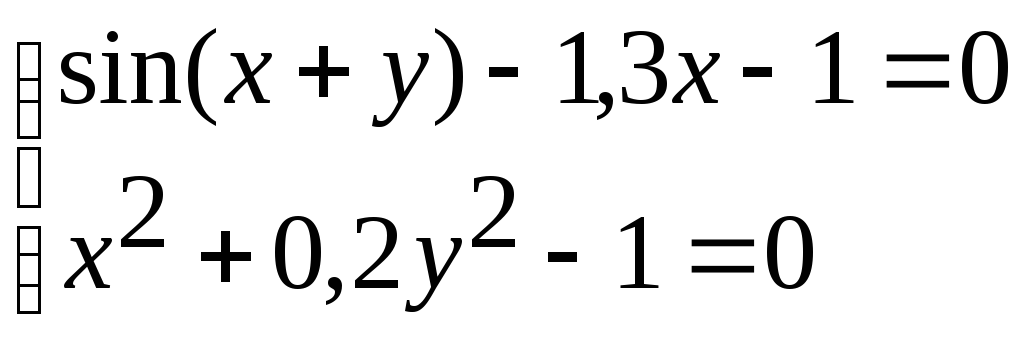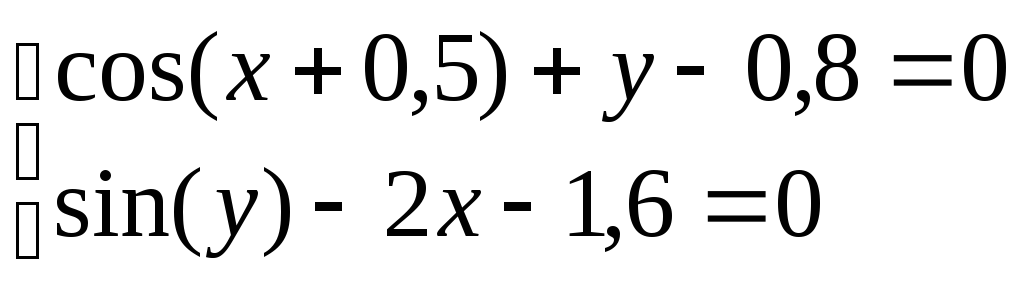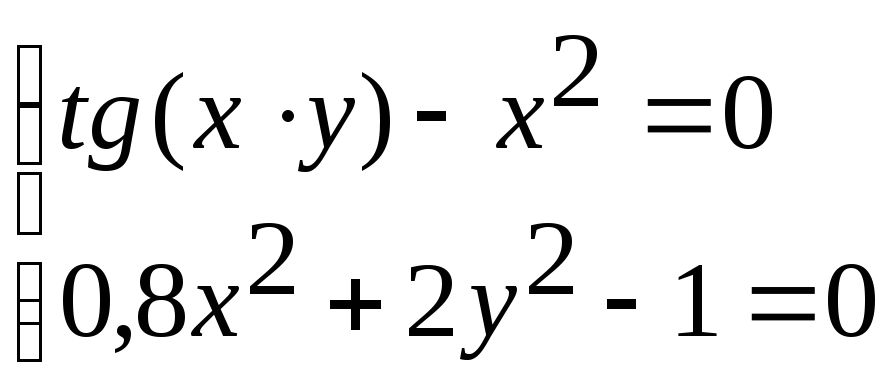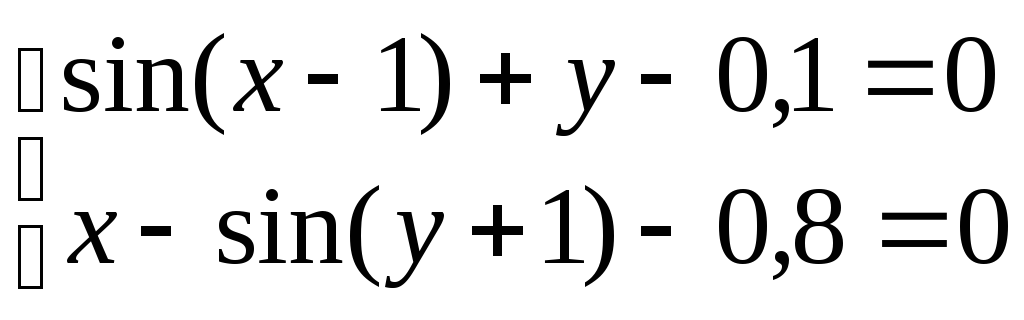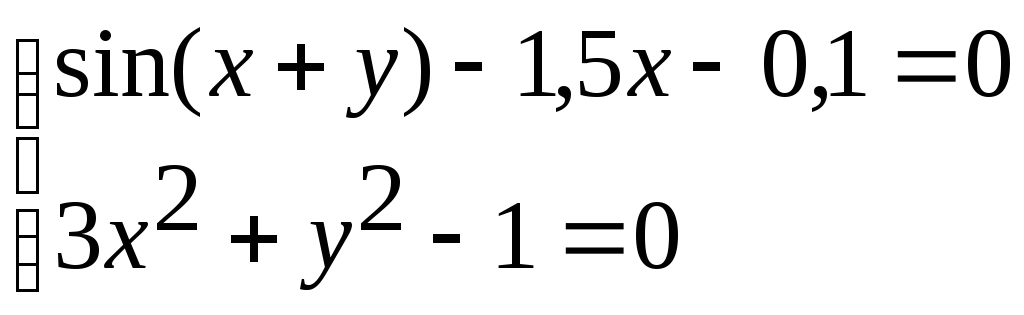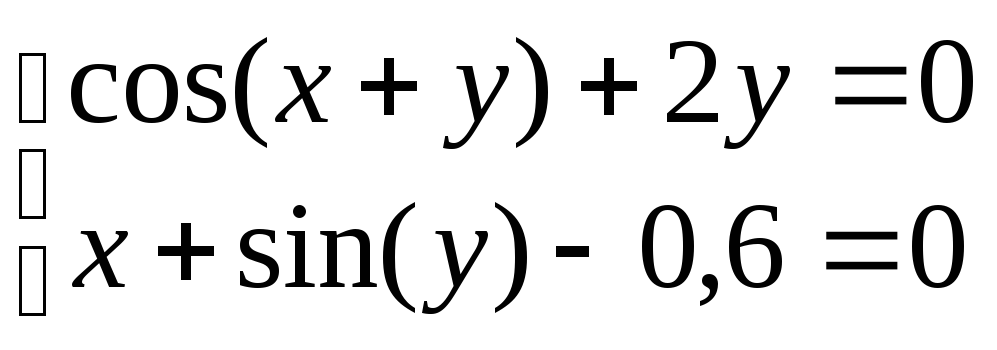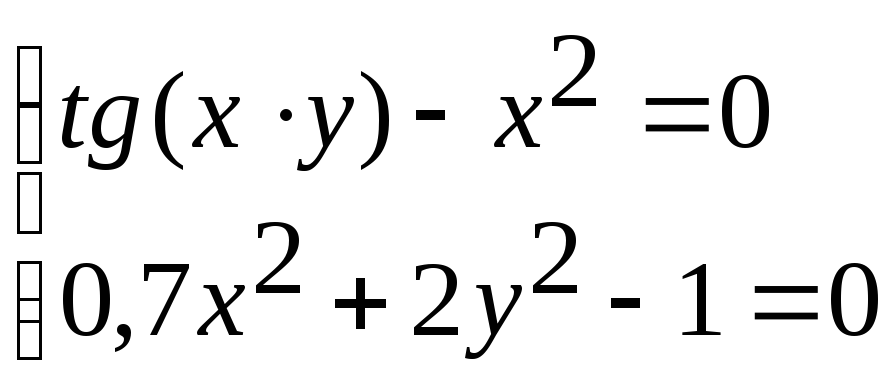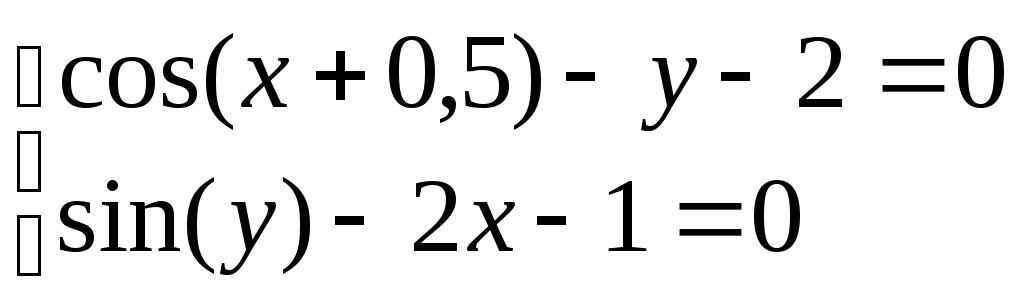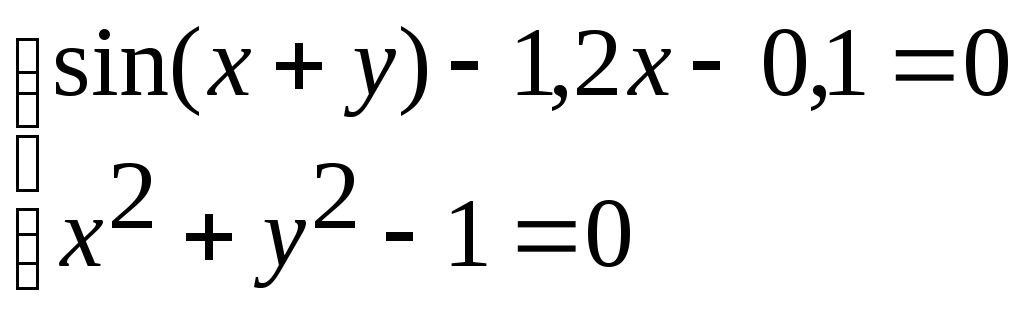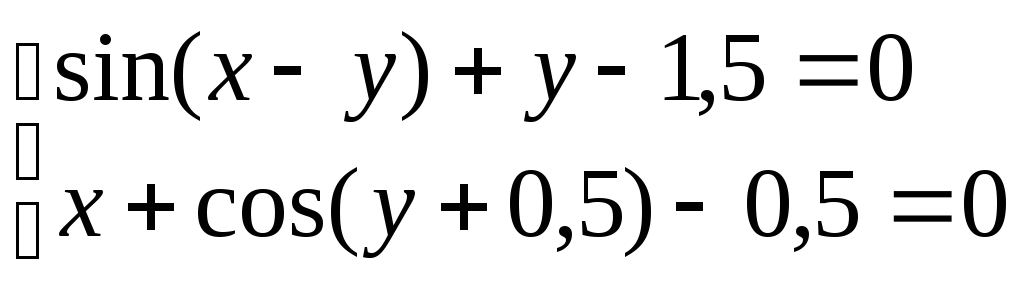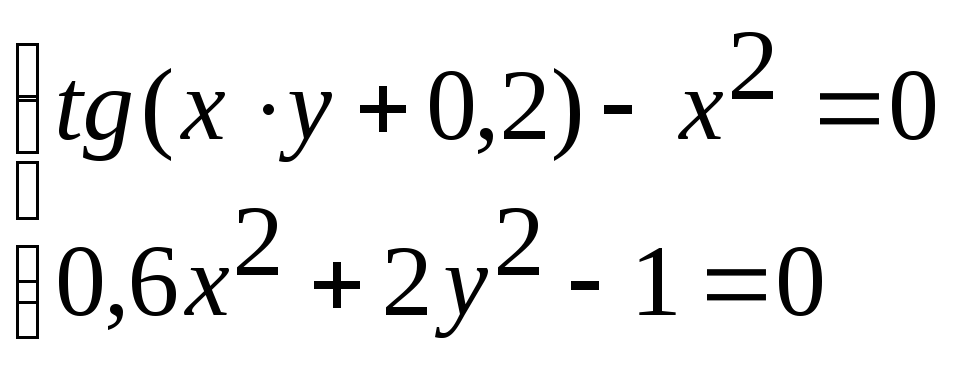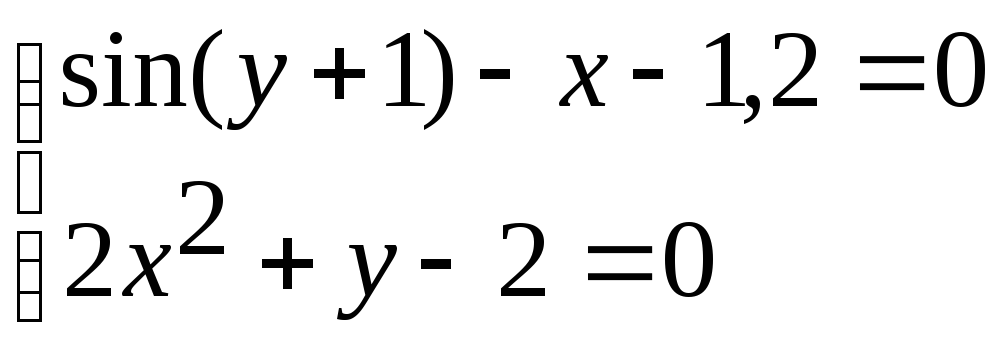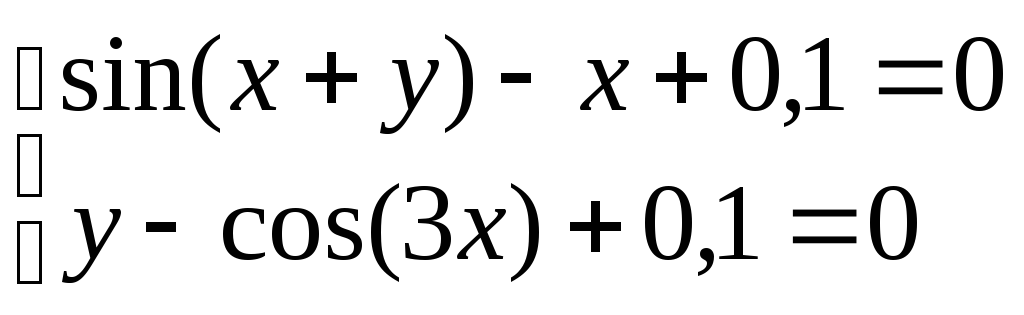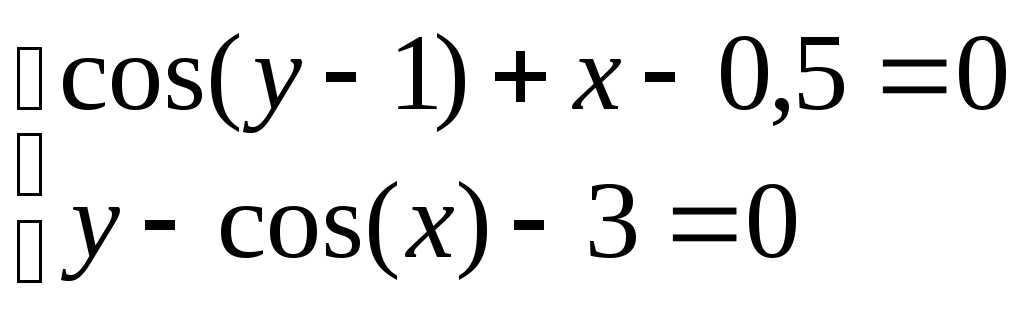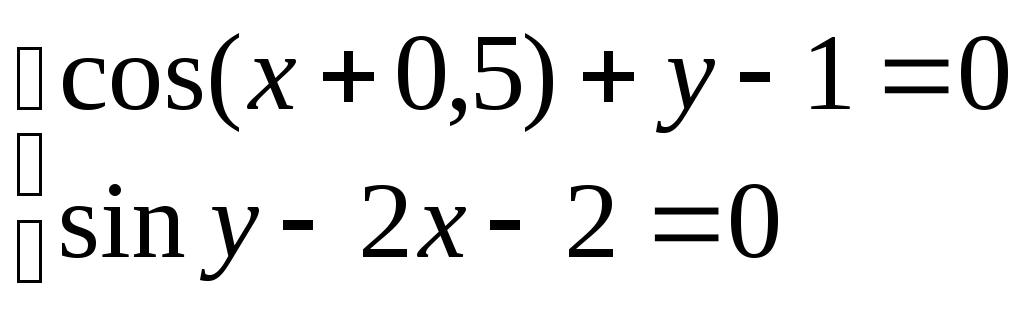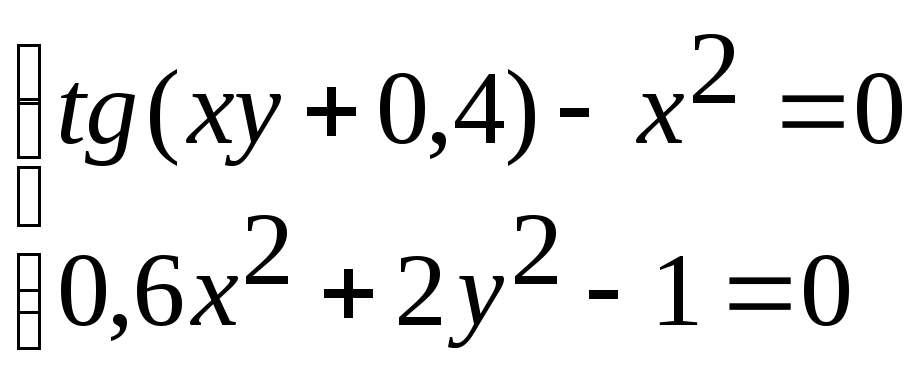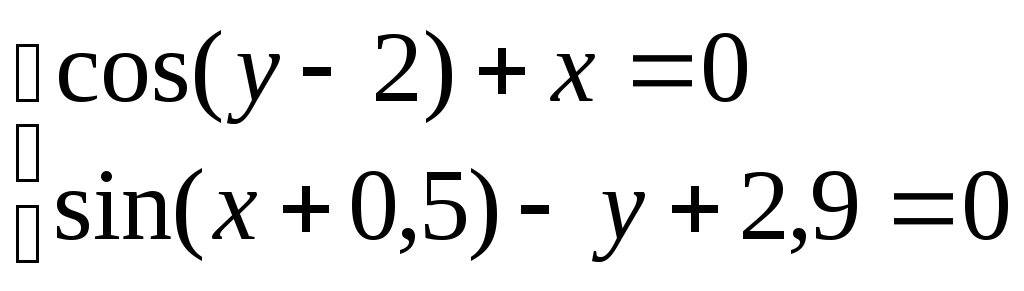- •Посібник з інформатики і системології
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця
- •1.1. Теоретична частина
- •1.2. Завдання для виконання лабораторної роботи
- •1.3 Приклад виконання роботи
- •1. Друкування та форматування тексту
- •2. Складання списків та їх форматування Кондитерська фабрика
- •3.Створення таблиці
- •4. Користування об’єктами WordArt
- •5. Створення формул
- •6. Складання блок-схеми
- •Питання для самоконтролю
- •Тема 2. Використання табличного процесора ms Excel в практичній роботі фахівця
- •2.1. Теоретична частина
- •2.2. Типи даних ет Excel
- •2.3. Сортування та фільтрація даних
- •2.4. Статистична обробка експериментальних даних на еп Excel (Завдання №1)
- •2.5. Завдання для виконання роботи
- •2.6. Приклад виконання роботи
- •2.7. Питання для самоконтролю
- •Тема 3. Алгоритмізація фахових задач та їх програмування на мові Pascal for Windows
- •3.1. Алгоритми
- •Фігури блок-схем
- •А) б)
- •3.2. Основи програмування на мові Pascal for Windows
- •3.3. Завдання для виконання лабораторної роботи
- •Завдання по темі
- •3.5. Питання для самоконтролю
- •Тема 4. Використання системи MathCad для розв’язування фахових задач
- •4.1. Загальні положення
- •4.2. Основи роботи в MathCad
- •1. Визначення змінних та їх результатів
- •4.3. Графічні об’єкти
- •В. Графічний вигляд функції
- •4.4. Символьний режим роботи
- •4.5. Завдання до виконання лабораторних робіт
- •Варіанти завдань
- •Варіанти до завдання 1
- •Варіанти до завдання 2
- •Варіанти до завдання 3
- •Варіанти завдання 4
- •Варіанти до завдання 5
- •4.6. Питання для самоконтролю
- •Тема 5. Розв’язування систем лінійних алгебраїчних рівнянь
- •5.1. Завдання до виконання роботи
- •Варіанти завдань
- •5.2. Питання для самоконтролю
- •Тема 6. Розв’язок нелінійних рівнянь та їх систем
- •6.1. Загальні положення
- •6.2. Етапи відокремлення коренів
- •6.3. Способи уточнення коренів
- •6.3.1. Метод половинного ділення (дихотомії)
- •6.3.2. Уточнення коренів методом хорд
- •6.3.3. Уточнення кореня методом дотичних (Ньютона)
- •6.3.4. Ітераційний метод уточнення кореня
- •6.3.5. Система нелінійних рівнянь
- •Варіанти завдань
- •6.4. Питання для самоконтролю
- •Тема 7. Інтерполяція і апроксимація функцій заданих таблично
- •7.1. Постановка задачі
- •7.2. Інтерполяційний поліном Лагранжа
- •7.3. Табличний метод застосування полінома Лагранжа
- •7.4. Інтерполяційні формули Ньютона
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •7.5. Обернена інтерполяція
- •Обернена інтерполяція
- •7.6. Апроксимація функцій методом найменших квадратів
- •7.7. Нелінійна апроксимація
- •Експоненціальна апроксимація
- •Варіанти завдань
- •7.9. Питання для самоконтролю
- •Тема 8. Чисельне диференціювання та інтегрування функцій
- •8.1. Наближене диференціювання
- •Диференціювання функції на базі
- •Варіанти завдань
- •8.3. Питання для самоконтролю
- •Тема 9: Чисельне інтегрування звичайних диференційних рівнянь
- •9.1. Загальні поняття
- •9.2. Метод Ейлера
- •9.3. Метод Рунге-Кутта
- •9.4. Інтегрування диференційних рівнянь інструментарієм системи MathCad
- •Функції rkfixed, Bulstoer таRkadapt
- •9.5. Завдання до виконання роботи
- •Варіанти завдань
- •9.6. Питання для самоконтролю
- •Тема 10. Чисельні методи оптимізації
- •10.1. Постановка задачі
- •10.2. Постановка задачі лінійного програмування
- •10.3. Геометрична інтерпретація злп
- •Графічний розв’язок злп
- •10.4. Симплекс-метод розв’язку злп
- •10.5. Розв’язок злп з допомогою ms Excel
- •Варіанти завдань
- •10.6. Транспортна задача
- •10.6.1. Постановка задачі
- •10.6.2. Метод північно-західного кута
- •Варіанти транспортної задачі
- •10.7. Питання для самоконтролю
- •Тема 11. Власні значення та власні вектори
- •11.1. Загальні поняття
- •11.2. Власні значення
- •11.3 Власні вектори
- •11.4 Знаходження найбільшого власного числа
- •11.5 Завдання
- •Варіанти завдань
- •11.6 Питання для самоперевірки
- •Література
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця 4
6.3.5. Система нелінійних рівнянь
На відміну від СЛАР для систем нелінійних рівнянь (СНР) не існує прямих методів розв’язку, а тому їх розв’язують лише ітераційними способами. В загальній формі СНР записується так:
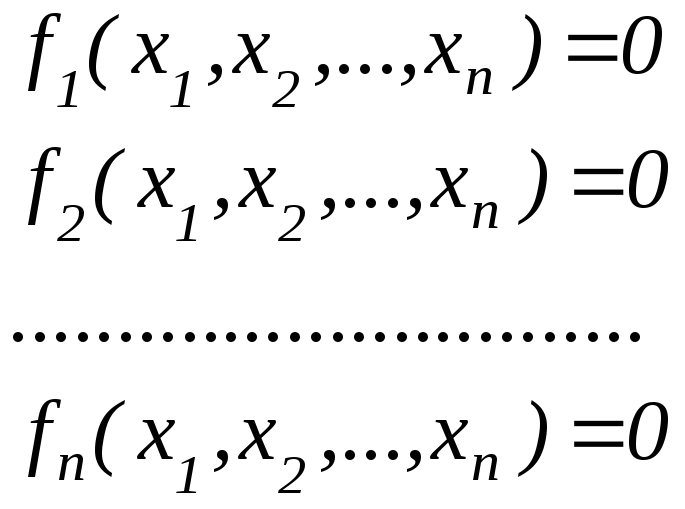 ,
(6.3)
,
(6.3)
або
в векторній формі
![]() ,
деХ
– вектор невідомих,
,
деХ
– вектор невідомих,
![]() – вектор-функція.
– вектор-функція.
Для одержання ітераційної формули створення процесу прямої ітерації приведемо систему (6.3) до вигляду:
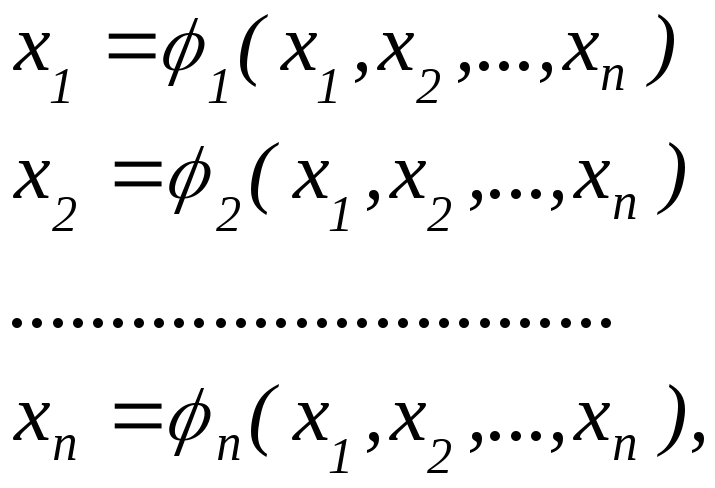
що
в векторній формі записують
![]() .
.
Задавши
початкове значення вектора невідомих
![]() ,
одержуємо ітераційний процес:
,
одержуємо ітераційний процес:![]() і т.д., допоки різниця норм векторівХ
на сусідніх ітераціях не стануть менше
наперед заданого малого числа :
і т.д., допоки різниця норм векторівХ
на сусідніх ітераціях не стануть менше
наперед заданого малого числа :
![]() .
.
Недоліком
таких процесів є те, що початкове значення
![]() потрібно вибирати лише взоні
збіжності
поблизу точки розв’язку. Цю зону
визначають із фізичних властивостей
процесів чи об’єктів, режим роботи яких
описується даною системою нелінійних
рівнянь. В двовимірному просторі зону
збіжності можна визначати графічно.
потрібно вибирати лише взоні
збіжності
поблизу точки розв’язку. Цю зону
визначають із фізичних властивостей
процесів чи об’єктів, режим роботи яких
описується даною системою нелінійних
рівнянь. В двовимірному просторі зону
збіжності можна визначати графічно.
Наступним
обмеженням застосування метода прямої
ітерації є те, що для створення збіжного
ітераційного процесу перетворення
![]() потрібно здійснити таким чином, щоб
потрібно здійснити таким чином, щоб
![]()
Наведемо приклад розв’язку СНР для двох невідомих:
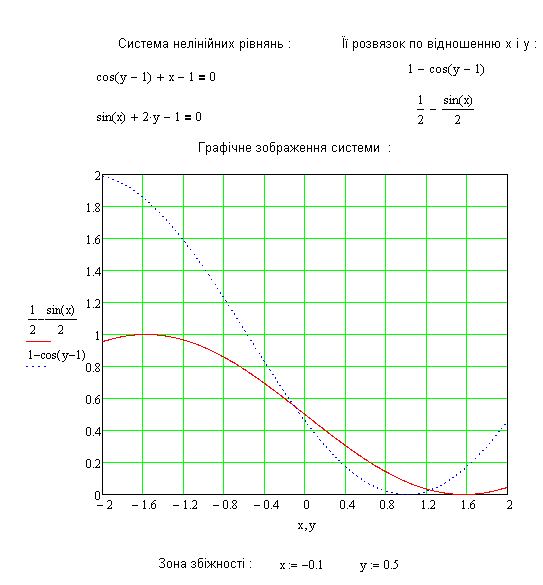
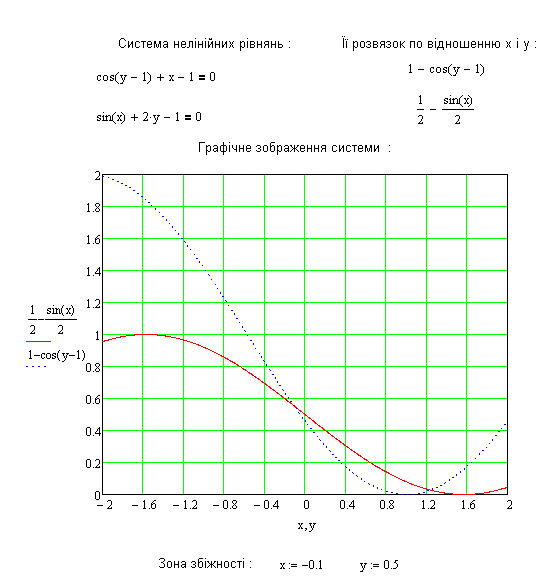

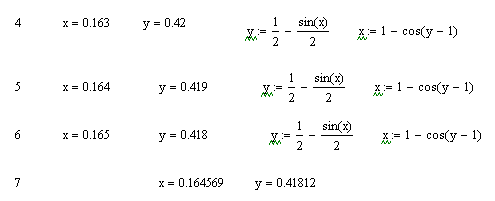
Найбільшого
поширення в інженерній практиці при
розв’язуванні СНР набув метод Ньютона,
який має ряд переваг перед іншими
ітераційними методами. В першу чергу –
це його значна швидкість збіжності. Для
побудови ітераційного процесу за цим
методом вектор-функцію
![]() розкладемо вn-вимірному
просторі в ряд Тейлора:
розкладемо вn-вимірному
просторі в ряд Тейлора:
![]()
Згідно
(6.3)
![]() .
Далі в цьому ряду
.
Далі в цьому ряду
![]() –вектор-функція,
розміщена в зоні збіжності;
–вектор-функція,
розміщена в зоні збіжності;
![]() –матриця
Якобі, яка складається із елементів, що
являють собою частинні похідні від усіх
рівнянь системи по усім невідомим;
–матриця
Якобі, яка складається із елементів, що
являють собою частинні похідні від усіх
рівнянь системи по усім невідомим;
– вектор-нев’язка,
яка наближає вектор
![]() до точки розв’язку системи;
до точки розв’язку системи;![]() – матриця Гессе, що складається із
частинних похідних другого порядку. В
двовимірному випадку маємо ці вектори
на рисунку 26.
– матриця Гессе, що складається із
частинних похідних другого порядку. В
двовимірному випадку маємо ці вектори
на рисунку 26.
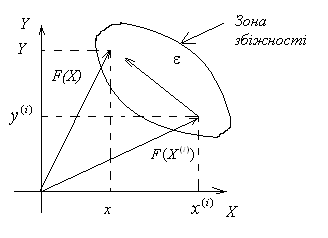
Рисунок 26 – Геометрична інтерпретація метода Ньютона
Враховуючи ітераційний процес, залишимо в ряду лише два перших елемента і одержимо значення вектора :
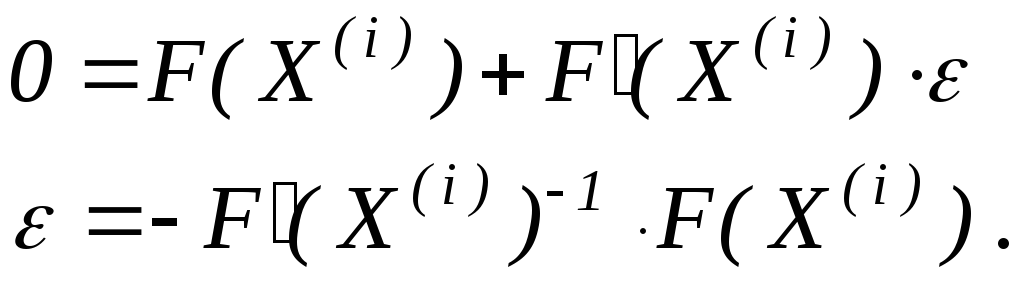
Звідси ітераційна формула буде мати вигляд:
![]() або:
або:
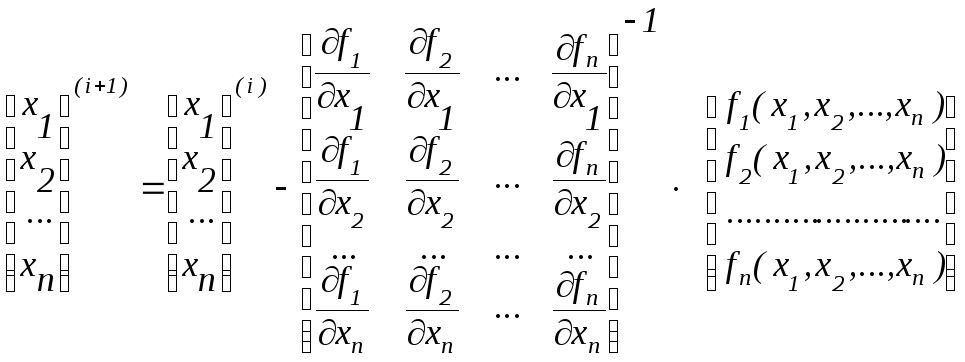 .
.
Таким
чином ітераційний процес по методу
Ньютона реалізуються схемою:
![]() і т.д.
і т.д.
Метод
збігається до точки розв’язку дуже
швидко (2-3 ітерації), але і для нього
існує проблема вибору початкового
вектора
![]() .
.
Застосуємо метод для попередньої задачі.



Перевіримо, розв’язок інструментарієм системи MathCad:

Варіанти завдань
Таблиця 13
|
№ вар |
Нелінійне рівняння f(x) |
№ вар |
Нелінійне рівняння f(x) |
|
1 |
|
14 |
|
|
2 |
|
15 |
|
|
3 |
|
16 |
|
|
4 |
|
17 |
|
|
5 |
|
18 |
|
|
6 |
|
19 |
|
|
7 |
|
20 |
|
|
8 |
|
21 |
|
|
9 |
|
22 |
|
|
10 |
|
23 |
|
|
11 |
|
24 |
|
|
12 |
|
25 |
|
|
13 |
|
26 |
|
Таблиця 14
|
№ вар |
Система нелінійних рівнянь |
№ вар |
Система нелінійних рівнянь |
|
1 |
|
14 |
|
|
2 |
|
15 |
|
|
3 |
|
16 |
|
|
4 |
|
17 |
|
|
5 |
|
18 |
|
|
6 |
|
19 |
|
|
7 |
|
20 |
|
|
8 |
|
21 |
|
|
9 |
|
22 |
|
|
10 |
|
23 |
|
|
11 |
|
24 |
|
|
12 |
|
25 |
|
|
13 |
|
26 |
|