
- •Посібник з інформатики і системології
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця
- •1.1. Теоретична частина
- •1.2. Завдання для виконання лабораторної роботи
- •1.3 Приклад виконання роботи
- •1. Друкування та форматування тексту
- •2. Складання списків та їх форматування Кондитерська фабрика
- •3.Створення таблиці
- •4. Користування об’єктами WordArt
- •5. Створення формул
- •6. Складання блок-схеми
- •Питання для самоконтролю
- •Тема 2. Використання табличного процесора ms Excel в практичній роботі фахівця
- •2.1. Теоретична частина
- •2.2. Типи даних ет Excel
- •2.3. Сортування та фільтрація даних
- •2.4. Статистична обробка експериментальних даних на еп Excel (Завдання №1)
- •2.5. Завдання для виконання роботи
- •2.6. Приклад виконання роботи
- •2.7. Питання для самоконтролю
- •Тема 3. Алгоритмізація фахових задач та їх програмування на мові Pascal for Windows
- •3.1. Алгоритми
- •Фігури блок-схем
- •А) б)
- •3.2. Основи програмування на мові Pascal for Windows
- •3.3. Завдання для виконання лабораторної роботи
- •Завдання по темі
- •3.5. Питання для самоконтролю
- •Тема 4. Використання системи MathCad для розв’язування фахових задач
- •4.1. Загальні положення
- •4.2. Основи роботи в MathCad
- •1. Визначення змінних та їх результатів
- •4.3. Графічні об’єкти
- •В. Графічний вигляд функції
- •4.4. Символьний режим роботи
- •4.5. Завдання до виконання лабораторних робіт
- •Варіанти завдань
- •Варіанти до завдання 1
- •Варіанти до завдання 2
- •Варіанти до завдання 3
- •Варіанти завдання 4
- •Варіанти до завдання 5
- •4.6. Питання для самоконтролю
- •Тема 5. Розв’язування систем лінійних алгебраїчних рівнянь
- •5.1. Завдання до виконання роботи
- •Варіанти завдань
- •5.2. Питання для самоконтролю
- •Тема 6. Розв’язок нелінійних рівнянь та їх систем
- •6.1. Загальні положення
- •6.2. Етапи відокремлення коренів
- •6.3. Способи уточнення коренів
- •6.3.1. Метод половинного ділення (дихотомії)
- •6.3.2. Уточнення коренів методом хорд
- •6.3.3. Уточнення кореня методом дотичних (Ньютона)
- •6.3.4. Ітераційний метод уточнення кореня
- •6.3.5. Система нелінійних рівнянь
- •Варіанти завдань
- •6.4. Питання для самоконтролю
- •Тема 7. Інтерполяція і апроксимація функцій заданих таблично
- •7.1. Постановка задачі
- •7.2. Інтерполяційний поліном Лагранжа
- •7.3. Табличний метод застосування полінома Лагранжа
- •7.4. Інтерполяційні формули Ньютона
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •7.5. Обернена інтерполяція
- •Обернена інтерполяція
- •7.6. Апроксимація функцій методом найменших квадратів
- •7.7. Нелінійна апроксимація
- •Експоненціальна апроксимація
- •Варіанти завдань
- •7.9. Питання для самоконтролю
- •Тема 8. Чисельне диференціювання та інтегрування функцій
- •8.1. Наближене диференціювання
- •Диференціювання функції на базі
- •Варіанти завдань
- •8.3. Питання для самоконтролю
- •Тема 9: Чисельне інтегрування звичайних диференційних рівнянь
- •9.1. Загальні поняття
- •9.2. Метод Ейлера
- •9.3. Метод Рунге-Кутта
- •9.4. Інтегрування диференційних рівнянь інструментарієм системи MathCad
- •Функції rkfixed, Bulstoer таRkadapt
- •9.5. Завдання до виконання роботи
- •Варіанти завдань
- •9.6. Питання для самоконтролю
- •Тема 10. Чисельні методи оптимізації
- •10.1. Постановка задачі
- •10.2. Постановка задачі лінійного програмування
- •10.3. Геометрична інтерпретація злп
- •Графічний розв’язок злп
- •10.4. Симплекс-метод розв’язку злп
- •10.5. Розв’язок злп з допомогою ms Excel
- •Варіанти завдань
- •10.6. Транспортна задача
- •10.6.1. Постановка задачі
- •10.6.2. Метод північно-західного кута
- •Варіанти транспортної задачі
- •10.7. Питання для самоконтролю
- •Тема 11. Власні значення та власні вектори
- •11.1. Загальні поняття
- •11.2. Власні значення
- •11.3 Власні вектори
- •11.4 Знаходження найбільшого власного числа
- •11.5 Завдання
- •Варіанти завдань
- •11.6 Питання для самоперевірки
- •Література
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця 4
Тема 5. Розв’язування систем лінійних алгебраїчних рівнянь
Систему n лінійних алгебраїчних рівнянь (СЛАР) з n невідомими можна представити у вигляді:
|
|
Ця система в матричному представленні має вигляд:
|
Ах = b, |
або
|
|
де а – матриця коефіцієнтів системи;
х – вектор невідомих;
b – вектор вільних членів.
Розв’язком
СЛАР є сукупність чисел
![]() ,
які при підстановці їх на місце
,
які при підстановці їх на місце![]() перетворюють всі рівняння (5.1) в тотожність.
перетворюють всі рівняння (5.1) в тотожність.
Якщо
визначник матриці А
не дорівнює 0, систему називають сумісною.
При
![]() СЛАР немає розв’язку (система несумісна).
СЛАР немає розв’язку (система несумісна).
Всі методи розв’язку сумісних СЛАР поділяються на прямі і ітераційні. В прямих методах розв’язок одержують за цілком певної кількості використаних арифметичних дій. До цих методів відносяться метод виключення невідомих Гауса, застосування формул Крамера, різні методи обернення матриць коефіцієнтів системи (рисунок 18-а).
Недоліком прямих методів розв’язку СЛАР є те, що зі збільшенням порядку системи збільшується похибка одержаного результату за рахунок збільшення операцій з неточними числами.
В ітераційних методах розв’язок системи знаходять в результаті багаторазових повторень однотипних операцій (ітерацій). Збільшуючи кількість таких повторень можна одержати результат з будь-якою наперед заданою точністю. Тому найчастіше при одержанні розв’язку СЛАР на комп’ютері застосовують саме ітераційні методи. До них відносяться прямий ітераційний метод, метод Зейделя, різного роду рекурентні методи.
Так як прямі методи досить детально вивчалися в курсі вищої математики, розглянемо побудову простого ітераційного процесу. Для одержання його ітераційної формули розв’яжемо кожне рівняння системи (5.1) по відношенню до свого невідомого. Тобто перше рівняння розв’яжемо по відношенню до х1, друге по відношенню до х2 і т.д. Одержимо систему:
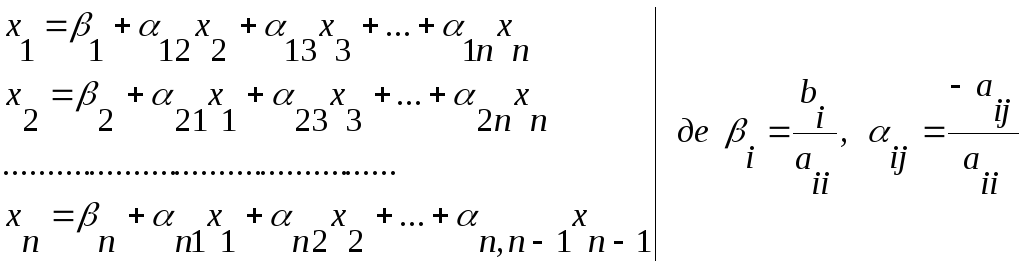 .
.
У вигляді матриць вона має вигляд:
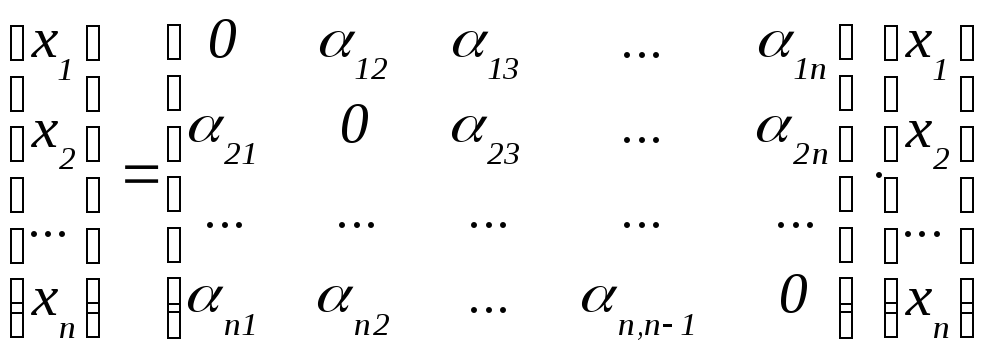 або
або
![]() .
.
Якщо тепер задатись початковим значенням Х(0), то можна одержати ітераційний процес:
![]() і
т.д. допоки елементи вектора Х
на двох сусідніх ітераціях з заданою
точністю не стануть близькими один до
одного (рисунок 18-б).
і
т.д. допоки елементи вектора Х
на двох сусідніх ітераціях з заданою
точністю не стануть близькими один до
одного (рисунок 18-б).
Такий
ітераційний процес буде збіжним при
будь-якому значенні Х(0),
якщо в системі (5.1) модуль діагональних
коефіцієнтів в кожному рівнянні буде
не меншим, ніж сума модулів побічних
коефіцієнтів цих же рівнянь:
![]() .
.
До такого вигляду можна привести будь-яку СЛАР, у якої не особлива матриця А, з допомогою законів лінійного комбінування:
розв’язок СЛАР не зміниться, якщо будь-яке її рівняння помножити на числову величину:
розв’язок СЛАР не зміниться, якщо поміняти місцями будь-які два рівняння;
розв’язок СЛАР не зміниться, якщо будь-яке рівняння замінити сумою (різницею) двох інших рівнянь.
Враховуючи
це, на практиці початковий вектор
невідомих для спрощення беруть в початку
координат
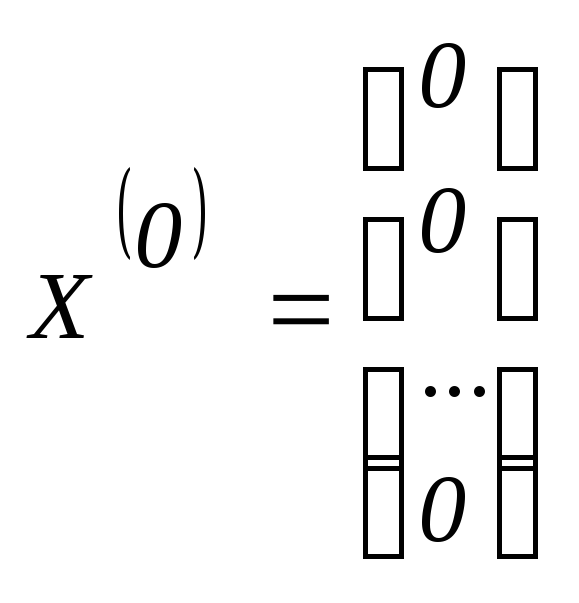 .
.
Ітераційний процес приведений на рисунку 18-б.

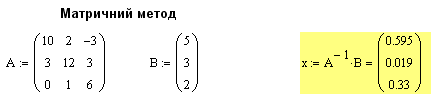
Перевірка:
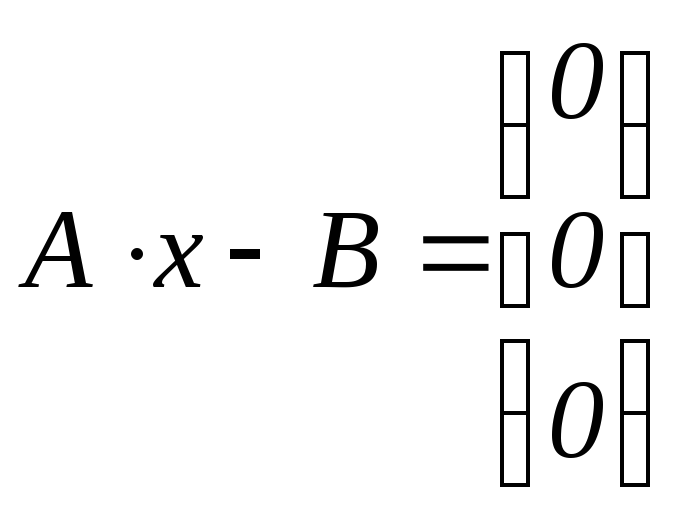 .
.


Умова
збіжності ітераційного процесу
виконується, т.я norme(![]() )<1.
)<1.
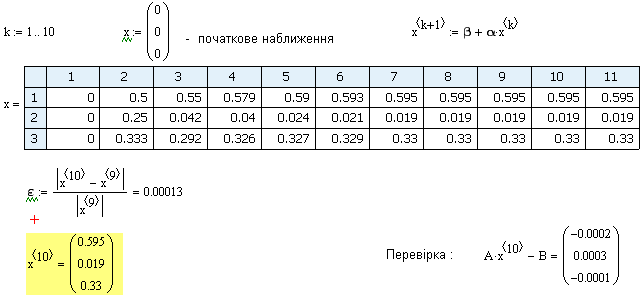
Покроковий розв’язок:

в) Перевірка за допомогою вмонтованих функцій
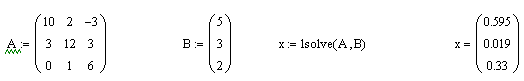


Рисунок 18 – Приклади рішення СЛАР

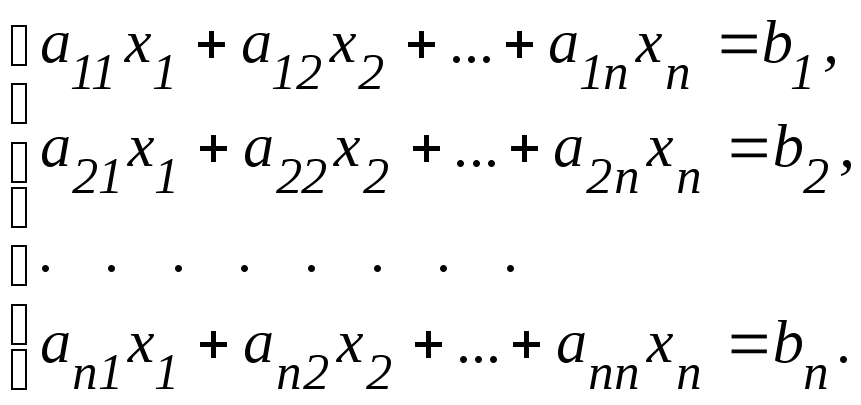 (5.1)
(5.1)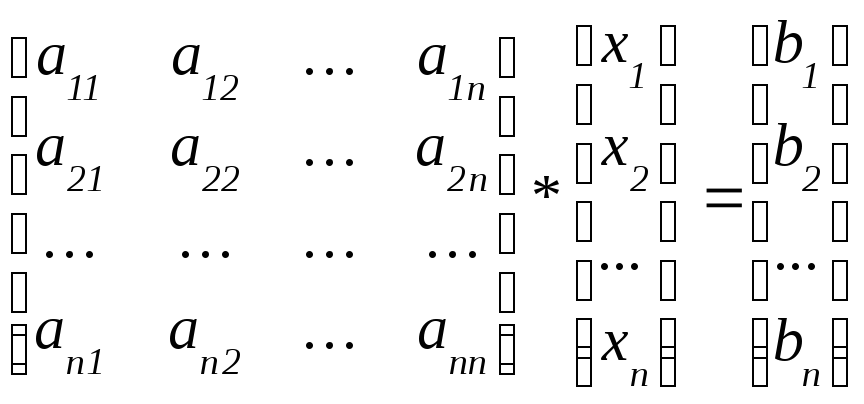 ,
,