6.3. Способи уточнення коренів

6.3.1. Метод половинного ділення (дихотомії)

Це найпростіший метод уточнення коренів. Його сутність полягає в наступному.

Відрізок ізоляції кореня рівнянняділимо навпіл і в серединній точціс знаходимо значення функції . Далі в точкус переносимо одну із точок a або b, в якій знак функції співпадає зі знаком функції в точці с. Таким чином, корінь рівняння залишається в двічі звуженому діапазоні . Тобто,

1. якщо 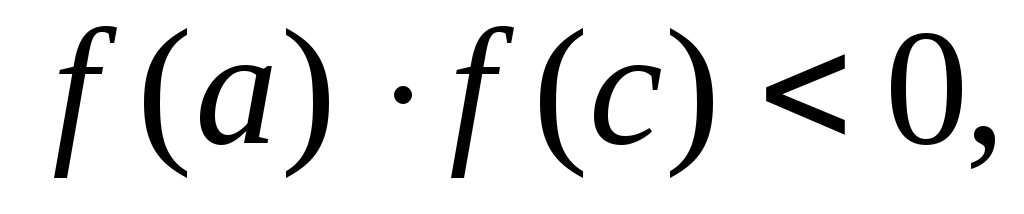то відбувається заміна точок;

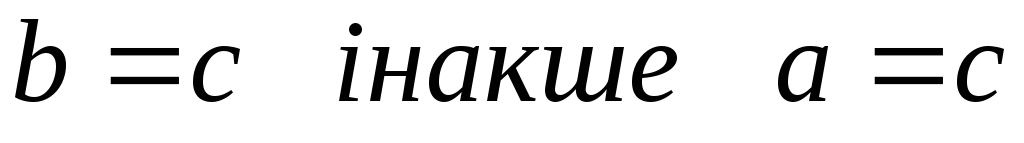2. або якщо 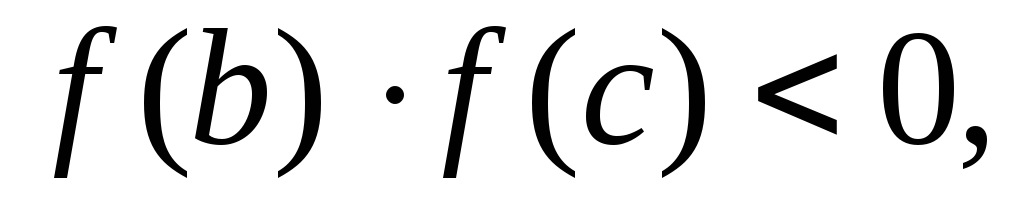то відбувається заміна точок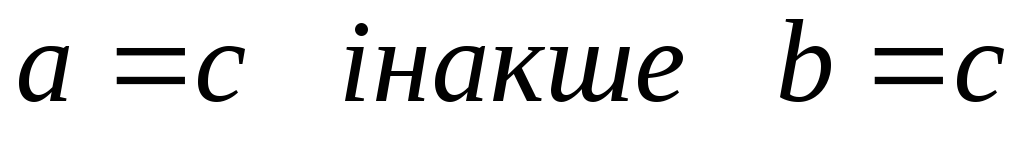

Процес ділення продовжуємо до тих пір, поки значення функції в точціс з заданою точністю не стане близьким до нуля, тобто Хід ітераційного процесу представлений на рисунку 22. Черезn ітерацій інтервал буде звужений вразів.

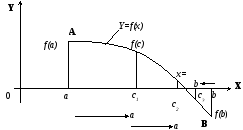
Рисунок 22 – Хід ітераційного процесу в методі дихотомії

Приклад розв’язку рівняння приведений далі:

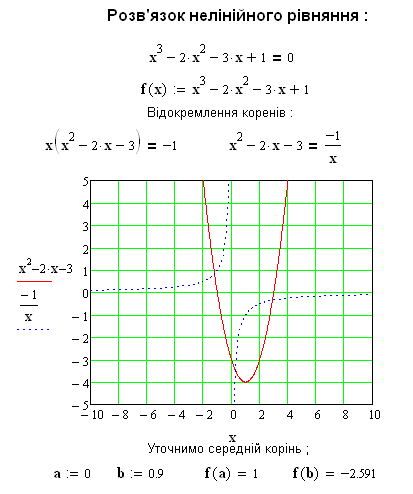
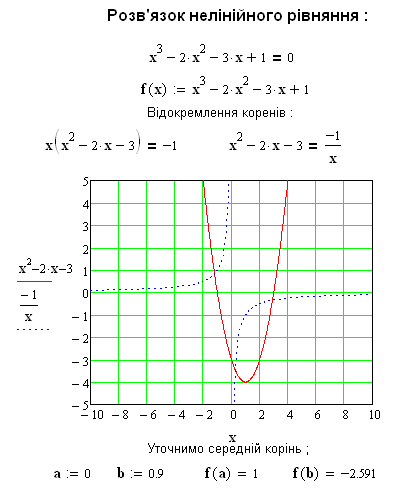
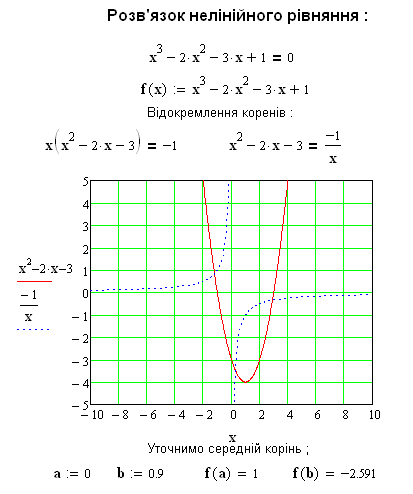
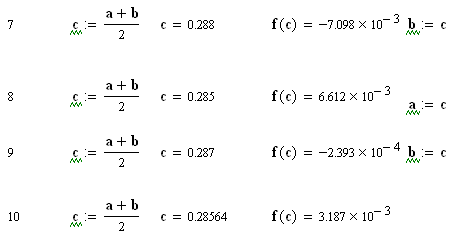
6.3.2. Уточнення коренів методом хорд

В методі дихотомії інтервал ділився навпіл. Процес був би більш ефективним, якби цей інтервал ділився в пропорції. В цьому випадку точкас на кожній ітерації була б ближче до точки кореня , ніж в методі половинного ділення. Ця точка відповідає точці перетину вісіОХ хордою, що зв’язує точки А та В (рисунок 21).

Для одержання ітераційної формули цього методу використаємо рівняння прямої, що з’єднує точки та:

.

Згідно з рисунком 23 визначаємо:

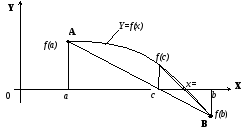
Рисунок 23 – Геометрична інтерпретація методу хорд

Враховуючи, що в точці кореня, маємо рівняння прямої АВ, тобто хорди.

Звідси .

Ітераційний процес по цій формулі ведуть допоки модуль значення функції в новій точці а стане менше наперед заданого числа : .

Приклад застосування методу хорд для наводиться далі.

6.3.3. Уточнення кореня методом дотичних (Ньютона)

Якщо метод хорд лінеаризував функцію хордою, метод Ньютона лінеаризує її дотичною в точціa або b (рисунок 24).

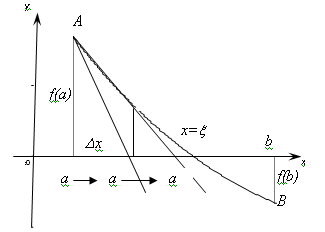
Рисунок 24 – Графічне представлення методу дотичних

При використанні цього методу дуже важливо правильно вибрати точку (a або b) його застосування. Як видно із рисунка 24 дотична з точки А буде наближати точку а до кореня, чого зовсім не можна сказати про дотичну в точці В. Точкою цього процесу потрібно вибрати ту із них, для якої знак функції та знак другої її похідної співпадають: .

Для виведення ітераційної формули для цього методу розкладено в ряд Тейлора функцію в точці кореня:

де – величина на осіОХ, що наближає початкову точку (a або b) до кореня .

Враховуючи ітераційний процес, залишимо в ряду лише два перші члени: . Нуль в лівій частині рівності записаний тому, що в точці кореня. Звідси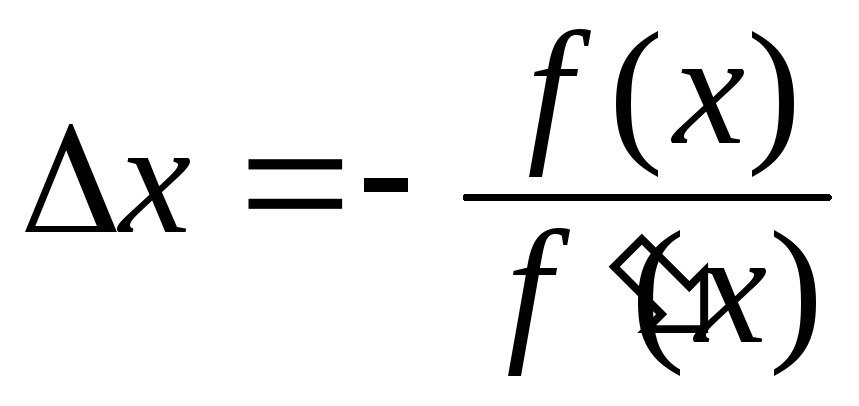. А нове наближення кореня.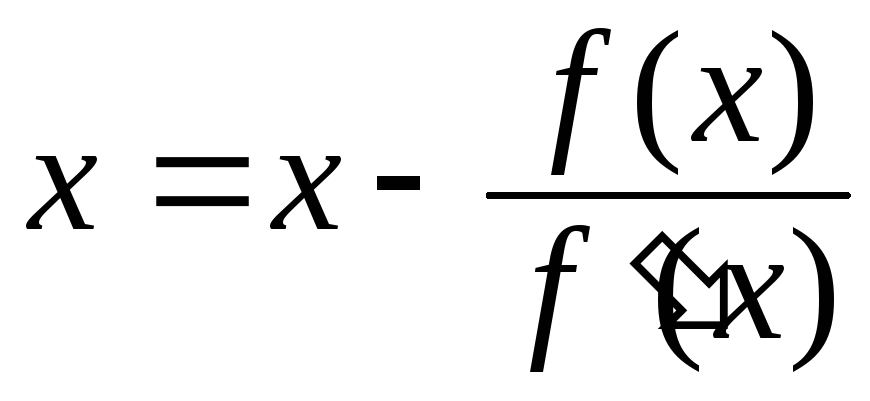

Враховуючи знак другої похідної в точках a або b, вибираємо для інтерполяційного процесу по цьому методу одну з формул:

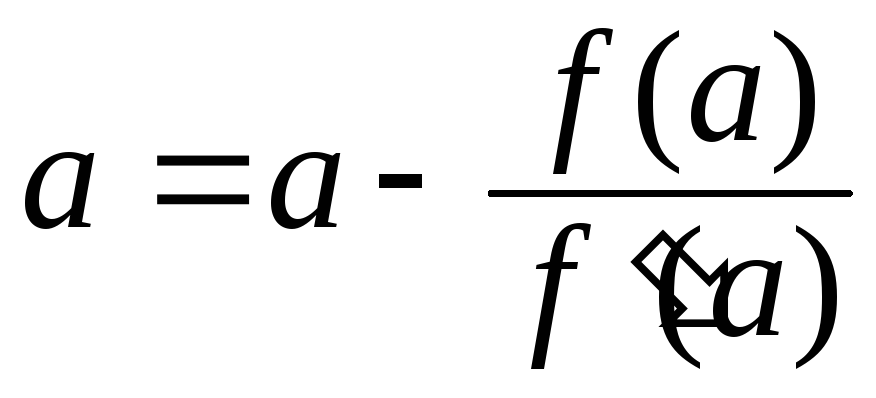або .

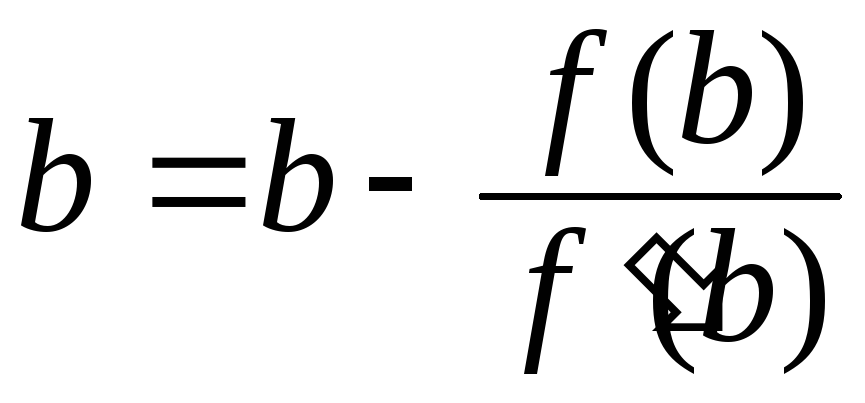Далі наводимо застосування метода:

6.3.4. Ітераційний метод уточнення кореня

Для ітераційного уточнення кореня рівняння приводять до виглядутаким чином, щоб виконувалась нерівність:.

Тоді задавши значенняa або b, одержуємо ітераційний процес:

і т.д. доти, поки .

В залежності від знака та величини ітераційний процес може бути монотонно збіжним (рисунок 25-а), збіжним коливним (рисунок 25-б), монотонно розбіжним (рисунок 25-в) та розбіжним коливним (рисунок 25-г).

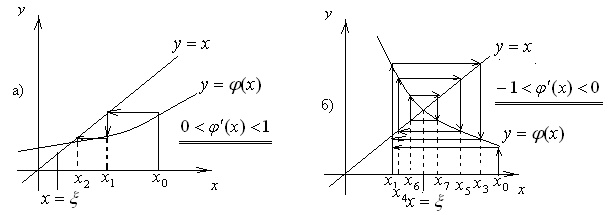
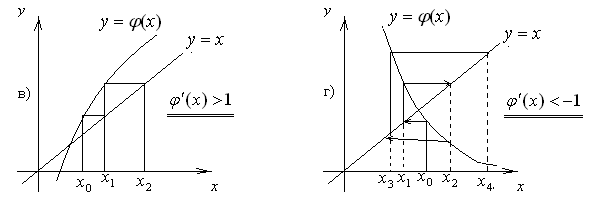
Рисунок 25 – Геометрична інтерпретація ітераційного процесу уточнення кореня нелінійного рівняння

Для рівняння варіації не дають значення меншого 1. І лише рівняннядаєзначення.

Сам ітераційний процес має вигляд:

Маємо коливний збіжний процес.

Перевіримо, розв’язок інструментарієм системи MathCad: