10.7. Питання для самоконтролю

1. Що таке задача оптимізації?

2. Проблеми оптимізації.

3. Критерій оптимальності.

4. Цільова функція.

5. Безумовні задачі оптимізації.

6. Умовні задачі оптимізації.

7. Область допустимих розв’язків.

8. Задача лінійного програмування.

9. Геометрична інтерпретація ЗЛП.

10. Симплекс-метод розв’язку ЗЛП.

11. Критерії допустимості базиса в симплекс-методі.

12. Критерії оптимальності таблиці в симплекс-методі.

13.Критерій відсутності розв’язку в симлекс-методі.

14. Критерій існування ведучого існування в симплекс-методі.

15. Алгоритм перетворення симплекс-таблиці.

16. Транспортна задача.

17. Метод північно-західного кута.

18. Метод найменшої вартості.

19. Метод подвійної переваги.

20. Метод потенціалів в оптимізації опорного плану.

Тема 11. Власні значення та власні вектори

11.1. Загальні поняття

Досить багато технічних задач успішно розв’язуються з застосуванням власних значень та власних векторів. При дослідженні динамічних процесів власні значення моделі відповідають частотам коливань, а власні вектори характеризують форми цих коливань. При розрахунках конструкцій на стійкість власні значення дають змогу оцінити критичні навантаження, спричиняють втрату стійкості об’єктом.

Перевірка міцності конструкційного матеріалу вимагає знання, так званих головних напружень, що зумовлюють напружений стан у точці. В цьому випадку головні напруження відповідають власним значенням, а власні вектори визначають орієнтацію площин, по нормалі до яких ці напруження діють.

Раніше ми розглядали збіжність ітераційних процесів СЛАР. Такі процеси будуть збіжними лише тоді, коли в матриці коефіцієнтів системи всі власні значення по модулю будуть менші за одиницю. Саме тому систему приводять до вигляду, коли .

Лише в такій системі всі власні значення по модулю менші за одиницю.

11.2. Власні значення

Якщо матриця здійснює відображення вектора:, то найчастіше векторперетворюється у вектор, змінюючись по величині та повертаючись на деякий кут (рисунок 11.1). Однак для будь-якої матриціA можна в просторі знайти такі особливі вектори, які при множенні на цю матрицю міняють не лише довжину, але й зберігають напрям (рисунок 11.2). Такі вектори називаютьсявласними векторами матриці А, а напрями, по яким вони розміщуються називаються головними осями матриці. Коефіцієнти, що відповідають зміні довжин власних векторів при їх відображенні через матрицю А називаються власними значеннями матриці А.

Наведемо два простих приклади. Нехай маємо матрицю та два ненульових векторита.

Множення цих векторів на матрицю справа дають результат:

Рисунок 11.1 – Відображення вектора Х1 через матрицю А.

Рисунок 11.2 – Відображення вектора Х2 через матрицю А

Як видно з рисунку 11.2 видно, якщо маємо справу з власним вектором Х матриці А, то повинно виконуватися співвідношення: ,

де  – власне значення матриці А.

Розглянемо матричний запис:

або

Повернемось до матричного запису:

.

Одержана матриця здійснює гомоморфне відображення вектора Х на початок координат. Гомоморфне відображення дає зворотне зображення не однозначним, а Отже матриця являється особливою. А, власні значення такої матриці можна знайти з умови:

.

Цей визначник грає велику роль в теорії матриць і називається віковим визначником. При розкритті цього визначника одержуємо характеристичне рівняння n-ого степеню, розв’язок якого дає n, в загальному випадку, різних значень . Якщо матриця дійсна та симетрична, то всі  будуть являти собою дійсні числа. В інших випадках – можуть бути і комплексно-спряжені числа.

Після розкриття вікового визначника будемо мати поліном n-го степеню:

.

Тут

–слід матриці: ,

–сума діагональних мінорів другого порядку ,

–сума діагональних мінорів третього порядку .

В загальному випадку дорівнює сумі всіх загальних мінорівго порядку матриціА. Вільний член дорівнює визначнику матриціА.

Приклад. Знайти власні значення матриці

.

Для запису вікового визначника знайдемо :

;

;

.

Мінори формули одержані шляхом викреслювання рядка і стовпця, де розміщені елементи матриці.

Якщо розмірність матриці , мінори одержують викреслюваннямрядків та стовпців для елементів.

;

;

;

;

;

;

+++++=.

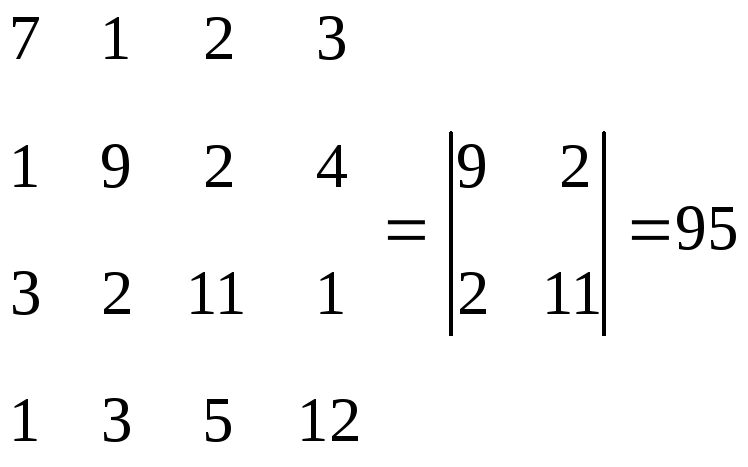
Сам визначник:

або

Розв’яжемо рівняння з допомогою символьного процесора MathCad:

.

Отже, для матриці маємо три власні числа;;.

Перевірка:

1. ;

2. ;

3.