7. Геометричний розподіл

Нехай проводяться незалежні випробування в кожному з яких ймовірність появи події А дорівнює р(0<р<1) і, отже, ймовірність її не появи q=l-р. Випробування закінчуються, як тільки з’явиться подія А. Таким чином, якщо подія А з’явилася в k-му випробуванні, то в попередніх k-1 випробуваннях вона не з’являлася.

Позначимо через Х дискретну випадкову величину - число випробувань, які потрібно провести до першої появи події А. Очевидно, що можливими значеннями Х є натуральні числа: х₁=1, х₂=2, ...

Нехай в перших k-1 випробуваннях подія А не наступила, а в k-му випробуванні з’явилася. Ймовірність цієї «складної події», за теоремою множення ймовірностей незалежних подій,

. (*)

Вважаючи k=1, 2, ... у формулі (*), отримаємо геометричну прогресію з першим членом р і знаменником q (0<q<1;

p, qp, q²p, …, q^k-1p, … (**)

З цієї причини розподіл (*) називають геометричним.

Легко переконатися, що ряд (**) сходиться і сума його дорівнює одиниці. Дійсно, сума ряду (**)

p/(1-q)=p/p=1/

Приклад, із гармати проводиться стрільба по цілі до першого влучення. Ймовірність влучення в ціль р=0,6. Знайти ймовірність того що, що влучення відбудеться при третьому пострілі.

Рішення. За умовою, р=0,6, q=0,4, k=3. Шукана ймовірність за формулою (*)

P=q^k-1p=0,4²*0,6=0,096.

8. Гіпергеометричний розподіл

Перш ніж дати визначення гіпергеометричного розподілу, розглянемо задачу. Хай в партії із N виробів є М стандартних (М<N). З партії випадково відбирають n виробів (кожний виріб може бути відібраний з однаковою ймовірністю), причому відібраний виріб перед відбором наступного не повертається до партії (тому формула Бернуллі тут незастосовна). Позначимо через Х випадкову величину - число m стандартних виробів серед n відібраних. Очевидно, можливі значення Х такі: 0, 1, 2, ..., min(M, n).

Знайдемо ймовірність того, що Х=m, тобто, що серед відібраних виробів рівно m стандартних. Використовуємо для цього класичне визначення ймовірності.

Загальне число можливих елементарних результатів випробування дорівнює числу способів, якими можна вийняти n виробів з N виробів, тобто числу сполучень .

Знайдемо число результатів, що сприяють події Х=m (серед узятих n виробів рівно m стандартних); m стандартних виробів можна вийняти з М стандартних виробів способами; при цьому інші n-m виробів повинні бути нестандартними; узяти ж n-m нестандартних виробів з N- m нестандартних виробів можнаспособами. Отже, число сприятливих результатів дорівнює (за правилом множення).

Шукана ймовірність дорівнює відношенню числа результатів, що сприяють події Х=m, до числа всіх елементарних результатів

. (*)

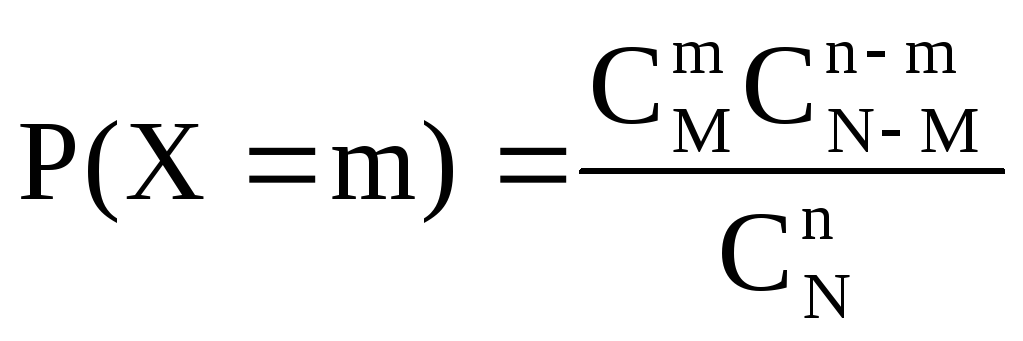Формула (*) визначає розподіл ймовірностей, який називають гіпергеометричним.

Враховуючи, що m – випадкова величина, робимо висновок, що гіпергеометричний розподіл визначається трьома параметрами: N, М, n. Іноді в якості параметрів цього розподілу розглядають N, n і р=М/N, де р – ймовірність того, що перший вийнятий виріб стандартний.

Відмітимо, що якщо n значно менше N (практично якщо n<0,1N, то гіпергеометричний розподіл дає ймовірності, близькі до ймовірностей, знайдених