9.3. Графік функції розподілу

Доведені властивості дозволяють представити, як виглядає графік функції розподілу безперервної випадкової величини.

Графік розташований в смузі, обмеженій прямими у=0, у=1 (перша властивість).

При зростанні х в інтервалі (а, b), у якому укладені всі можливі значення випадкової величини, графік підіймається вверх (друга властивість).

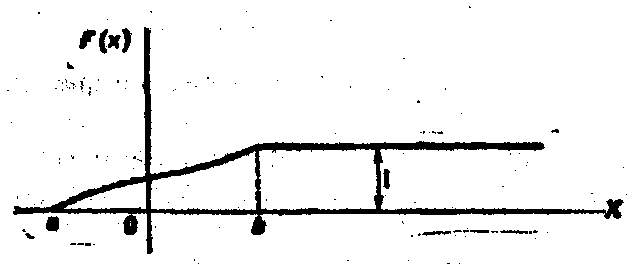
Рис. 1

При ординати графіка рівні нулю; приординати графіка рівні одиниці (третя властивість).

Графік функції розподілу безперервної випадкової величини зображений на рис. 1.

Зауваження. Графік функція розподілу дискретної випадкової величини має ступінчастий вигляд (рис. 2).

Приклад. Дискретна випадкова величина Х задана таблицею розподілу

X	1	4	8
p	0,3	0,1	0,6

Знайти функцію розподілу і накреслити її графік.

Розв’язок. Якщо то (третя властивість)

Якщо , то . Дійсно,Хможе прийняти значення 1 з ймовірністю 0,3.

Якщо , то . Дійсно, якщохзадовольняє нерівність , то дорівнює ймовірності події , яка може бути здійснена, коли Х прийме значення 1 (ймовірність цієї події дорівнює 0,3) або значення 4 (ймовірність цієї події дорівнює 0,1). Оскільки ці дві події несумісні, то за теоремою додавання ймовірностей ймовірність події рівна сумі ймовірностей 0,3+0,1=04.

Якщо , то. Дійсно, подія достовірна, отже, її ймовірність дорівнює одиниці.

Отже, функція розподілу аналітично може бути записана так:

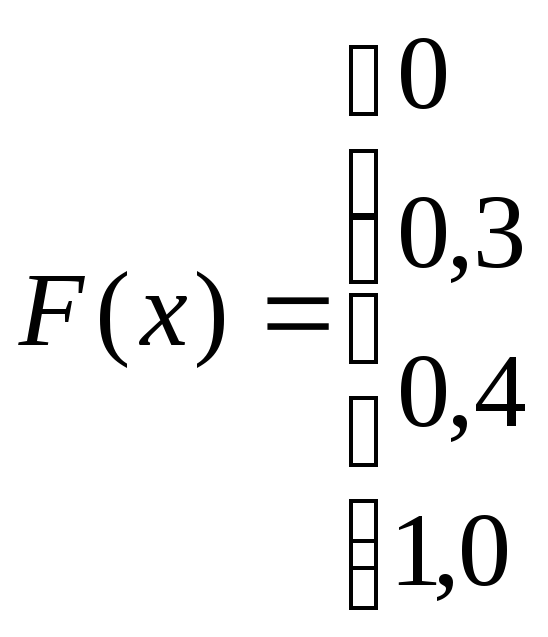
Графік цієї функції наведений на рис. 3.

Рис. 2.

Запитання для самоперевірки:

1. Дайте визначення випадкової величини.

2. Яку випадкову величину називають дискретною?

3. Яку випадкову величину називають неперервною?

4. Якими способами можна задати закон розподілу?

5. Як називають графічне зображення закону розподілу дискретної випадкової величини?

6. Дайте визначення біноміального закону розподілу. Чому його називають біноміальним?

7. При яких умовах для задання закону розподілу використовують асимптотичну формулу Пуассона?

8. Що називають потоком подій?

9. Які властивості притаманні найпростішим потокам подій?

10. У чому полягає властивість стаціонарності потоку?

11. У чому полягає властивість відсутності післядії?

12. У чому полягає властивість ординарності потоку?

13. Якою формулою можна описати властивості найпростішого потоку?

14. Дайте характеристику геометричного розподілу.

15. Дайте визначення і поясніть сутність функції розподілу випадкової величини.

16. Наведіть властивості функції розподілу.

17. Зобразіть графік функції розподілу.

ЧИСЛОВІ ХАРАКТЕРИСТИКИ ДИСКРЕТНИХ ВИПАДКОВИХ ВЕЛИЧИН

Як уже відомо, закон розподілу повністю характеризує випадкову величину. Однак часто закон розподілу невідомий і доводиться обмежуватися меншими відомостями. Іноді навіть вигідніше користуватися числами, які описують випадкову величину сумарно; такі числа називають числовими характеристикам випадкової величини. До числа важливих числових характеристик ставиться математичне сподіванння і дисперсія.

1. Математичне сподіванння дискретної випадкової величини

Математичне сподіванння, як буде показано далі, приблизно дорівнює середньому значенню випадкової величини. Для рішення багатьох задач досить зиати математичне сподіванння. Наприклад, якщо відомо, що математичне сподіванння числа оочок, що вибивають, у першого стрільця більше, ніж у другого, то перший стрілець у середньому вибиває більше оочок, чим другий, і, отже, стріляє краще другого. Хоча математичне сподіванння дає про випадкову величину значно менше відомостей, чим закон її розподілу, але для розв’язання задач, подібних наведеній й багатьох інших, знання математичного сподіванння виявляється достатнім.

Математичним сподіваннням дискретної випадкової величини називають суму добутків всіх її можливих значень на їхні імовірності.

Нехай випадкова величина Xможе приймати тільки значеннях_1, х₂,...,x_nймовірності яких відповідно рівнір₁, р₂, …, р_n. Тоді математичне сподіваннняМ(X)випадкової величиниXвизначається рівністю

.

Якщо дискретна випадкова величина Xприймає рахункову множину можливих значень, то

,

причому математичне сподіванння існує, якщо ряд у правій частині рівності сходиться абсолютно.

Зауваження. Із визначення слідує, що математичне сподіванння дискретної випадкової величини є невипадкова (постійна) величина. Рекомендуємо запам’ятати це твердження, тому що далі воно використається багаторазово. Надалі буде показано, що математичне сподіванння безперервної випадкової величини також є постійна величина.

Приклад 1. Знайти математичне сподіванння випадкової величиниX, знаючи закон її розподілу:

X	3	5	2
p	0,1	0,6	0,3

Розв’язок.Шукане математичне сподіванння дорівнює сумі добутків всіх можливих значень випадкової величини на їхні ймовірності:

.

Приклад 2. Знайти математичне сподіванння числа появ подіїАв одному випробуванні, якщо ймовірність подіїАдорівнюєр.

Розв’язок. Випадкова величинаХ– число появ подіїАв одному випробуванні – може приймати тільки два значення: (подія А наступила) з ймовірністюрі (подіяАне наступило) з ймовірністю . Шукане математичне сподіванння

.

Отже, математичне сподіванння числа появ події А одному випробуванні дорівнює ймовірності цієї події. Цей результат буде використаний нижче.