4. Біноміальний розподіл

• Хай проводиться п незалежних випробувань, в кожному з яких подія А може з’явитися або не з’явитися. Ймовірність настання події у всіх випробуваннях постійна і рівна р (отже, ймовірність непояви q=1-р). Розглянемо в якості дискретної випадкової величини Х число появ події А в цих випробуваннях.

Поставимо перед собою завдання знайти закон розподілу величини Х. Для її рішення потрібно визначити можливі значення Х і їх ймовірності . Очевидно, подія А в n випробуваннях може або не з’явитися, або з’явитися 1 раз, або 2 рази, ..., або n разів. Таким чином, можливі значення Х наступні: х₁=0, х₂=1, х₃=2, ...,_хn+1=n. Залишається знайти ймовірності wих можливих значень, для чого достатньо скористатися формулою Бернуллі:

, (*)

де 0, 1, 2, ..., n.

Формула (*) і є аналітичним вираженням шуканого закону розподілу.

Біноміальнимназивають розподіл ймовірностей, що визначається формулою Бернуллі. Закон названий біноміальним тому, що праву частину рівності (*) можна розглядати як загальний член розкладання бінома Ньютона:

.

Таким чином, перший член розкладання pⁿвизначає ймовірність настання даної події n разів в n незалежних випробуваннях; другий член визначає ймовірність настання події n-1 раз; … ; останній член qⁿвизначає ймовірність того, що подія не з’явиться жодного разу. Напишемо біноміальний закон у вигляді таблиці:

X	n	n-1	…	k	...	0
P					...

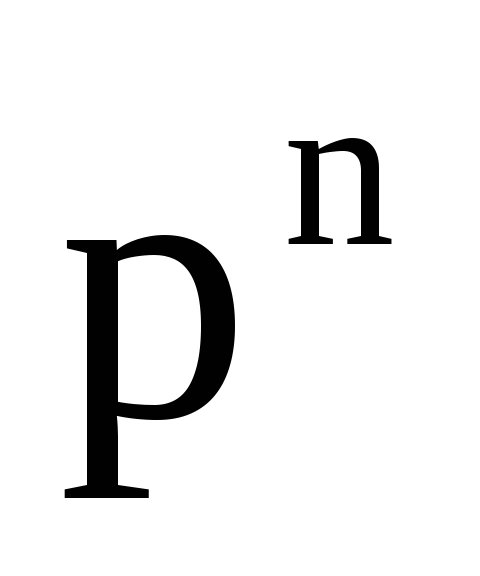
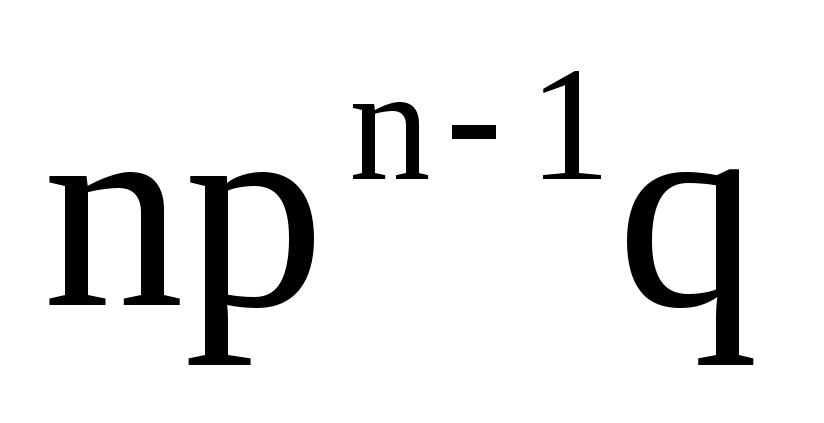
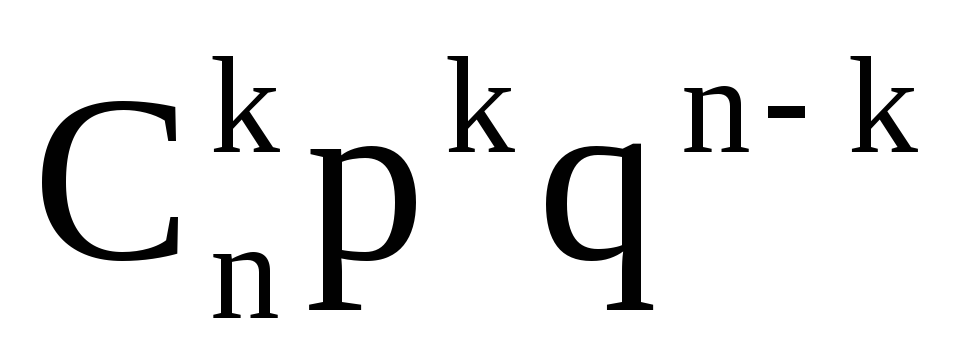
Приклад.Монета кинута 2 рази. Написати у вигляді таблиці закон розподілу випадкової величини Х - числа випадань „герба”.

Рішення. Ймовірність появи „герба» в кожному випробуванні р=1/2, отже, ймовірність непояви „герба”q=1-1/2=1/2.

При двох киданнях монети гербќ може з’явитися або 2 раз, або 1 раз, або зовсім не з’явитися. Таким чином, можливі ачения Х такі: х₁=2, х₂=1, х₃=0. Знайдемо ймовірності цих можливих значень за формулою Бернуллі:

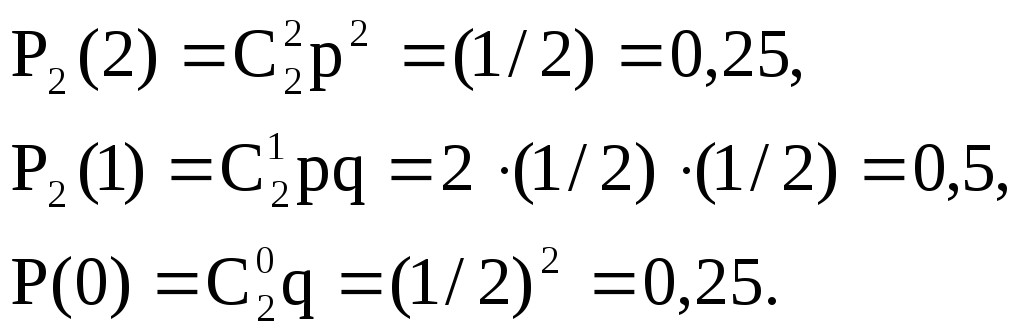
Напишемо шуканий закон розподілу:

Х	2	1	0
р	0,25	0,5	0,25

Контроль: 0,25+0,5+0,25=1.

5. Розподіл Пуассона

Нехай проводиться n незалежних випробувань, в кожному з яких ймовірність появи події А рівна р. Для визначення ймовірності k появ події A в цих випробуваннях використовують формулу Бернуллі. Якщо ж n велике, то користуються асимптотичною формулою Лапласа. Проте ця формула непридатна, якщо ймовірність події мала (р<0,1). В цих випадках (n велике, р малe) вдаються до асимптотичної формули Пуассона.

Отже, поставимо перед собою задачу знайти ймовірність того, що при дуже великому числі випробувань, в кожному з яких ймовірність настання події дуже мала, подія настане рівно k разів. Зробимо важливе допущення: добуток np зберігає постійне значення, а саме . Як буде виходити з подальшого, це означає, що середнє число появ події в різних серіях випробувань, тобто при різних значеннях n, залишається незмінним.

Скористаємося формулою Бернуллі для обчислення ймовірності, що цікавить нас:

.

Так як ,то. Отже

.

Взявши до уваги, що n має дуже велике значення, замість P_n(k) знайдемо. При цьому буде знайдено лише наближене значення відшукуваної ймовірності : n хоча й велике, але кінечне, а при відшуканні межі спрямуємо n до бескінечності. Відмітимо, що оскільки добуток nр зберігає постійне значення, то приймовірність.

Отже,

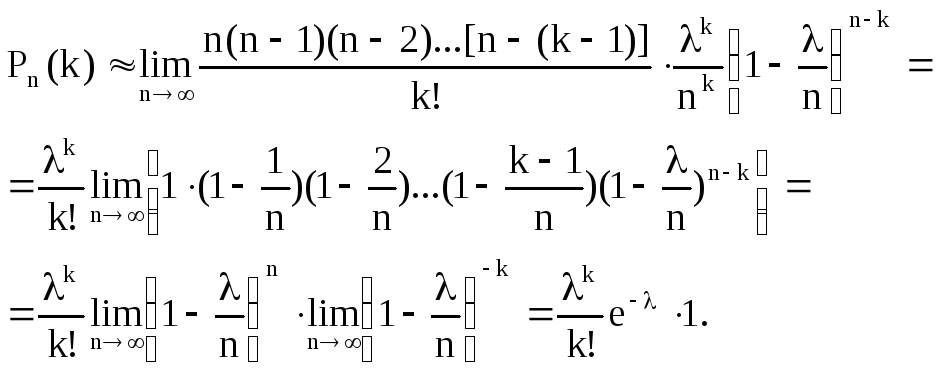
Таким чином (для простоти запису знак приблизної рівності опущено),

.

Ця формула виражає закон розподілу Пуассона ймовірностей масових (n велике) і рідких (р мале) подій.

Зауваження. Є спеціальні таблиці, користуючись якими можна знайти , знаючиі.

Приклад.Завод відправив на базу 5000 доброякісних виробів. Ймовірність того, що в дорозі виріб буде пошкоджений, дорівнює 0,0002. Знайти ймовірність того, що на базу прибудуть 3 непридатні вироби.

Рішення. За умовою, n=5000, р=0,0002, k=3. Знайдемо :

.

За формулою Пуассона шукана ймовірність приблизно дорівнює

.