Тема 3. Чисельне інтегрування
Лекція 5. Метод трапецій
Якщо функція f (x) безперервна на відрізку [a,b] й відома її первісна F (x), то певний інтеграл від цієї функції може бути обчислений по формулі
Ньютона-Лейбница:
∫b f (x)dx = F (b)− F (a), |
(5.1) |
a
де F′(x)= f (x). Однак, у багатьох випадках, виникають більші труднощі,
пов'язані зі знаходженням первісної, або ця задача не може бути вирішена елементарними способами. Тому в багатьох випадках буває важко або неможливо застосувати формулу (5.1). Крім того, подінтегральна функція
f (x) часто буває задана таблицею. Тому чисельні методи обчислення
інтегралів мають важливе значення.
Задача чисельного інтегрування функції полягає в обчисленні певного інтеграла на підставі ряду значень подінтегральної функції.
Чисельне обчислення однократного інтеграла називають механічною квадратурою, а подвійного - механічною кубатурою. Відповідні формули називають квадратурними й кубатурнимі формулами.
Постановка задачі
Нехай потрібно знайти певний інтеграл |
|
||
|
F = ∫b |
f (x)ρ(x)dx , ρ(x)> 0 |
(5.2) |
де функція f (x) |
a |
|
функція ρ(x) |
безперервна на відрізку [a,b], а вагарня |
|||
безперервна на інтервалі (a,b). Виразити інтеграл через елементарні функції вдається рідко, а компактний і зручний для доведення до числа відповідь виходить ще рідше. Тому звичайно заміняють f (x) на таку апроксимуючу функцію ϕ(x,a)≈ f (x), щоб інтеграл від її обчислювався в елементарних функціях.
Найчастіше f (x) заміняють деяким узагальненим інтерполяційним
багаточленом. Оскільки така апроксимація ленійна щодо параметрів, то функція при цьому заміняється деяким лінійним вираженням, коефіцієнтами якого служать значення функції у вузлах:
n |
|
f (x)= ∑ f (xi ) ϕi (x)+ r (x) |
(5.3) |
i=0
де r (x) – залишковий член апроксимації. Підставляючи (5.3) в (5.2), одержимо формулу чисельного інтегрування (квадратурну формулу):
38
n |
|
F = ∑ci f (xi )+ R , |
|
i=0 |
(5.4) |
|
|
ci = ∫b ϕi (x) ρ(x)dx , |
R = ∫b r (x) ρ(x)dx |
a |
a |
де величини xi – називають вузлами, ci |
– вагами, а R – погрішністю або |
залишковим членом формули. Інтеграл приблизно заміняється сумою, схожої на інтегральну суму, причому вузли й коефіцієнти цієї суми не залежать від
функції f (x). Інтерполяційний багаточлен (5.3) може бути не тільки
лагранжева, але й эрмитова типу; в останньому випадку в суму (5.4) увійдуть похідні функції у вузлах.
Найкраще вивчена заміна функції f (x) алгебраїчним багаточленом, що і розглянемо нижче.
Формула трапецій
Геометрична інтерпретація певного інтеграла F = ∫b f (x)dx полягає в
a
тому, що він чисельно дорівнює площі криволінійної трапеції обмеженою частиною осі абсцис, двома прямими x = a , x = b і подінтегральною кривою
y = f (x) (рис. 5.1).
R
y = f (x)
a |
b |
Рис. 5.1 Геометричні побудови для методу трапецій
Заміняючи приблизно функцію f (x) лінією, одержимо трапецію, площу якої дорівнює F 1 = 21 (b − a) ( f (a)+ f (b)), або
F = ∫b |
f (x)dx ≈ |
1 |
(b − a) ( f (a)+ f (b)). |
(5.5) |
|
2 |
|||||
a |
|
|
|
39
Формула (5.5) це формула трапецій для наближеного обчислення певного інтеграла. Помилка квадратурної формули – це площа рівна R . Знайдемо її погрішність.
Погрішність формули трапецій
Для цього розкладемо f (x) по формулі Тейлора, вибираючи середину
відрізка за центр розкладання й припускаючи наявність у функції необхідних по ходу міркувань безперервних похідних:
f (x)= f (x )+ (x − x ) f ′(x )+ |
1 |
(x − x )2 |
f ′′(x )+ ..., |
||||
2 |
|||||||
|
|
1 |
|
|
|
||
де |
x = |
(a + b) |
|
|
(5.6) |
||
2 |
|
|
|||||
|
|
|
|
|
|
||
Погрішність є різниця точного й наближеного значень інтеграла. Підставляючи в (5.5) розкладання (5.6) одержимо головний член погрішності:
R = ∫b |
f (x)dx − b − a |
( f (a)+ |
f (b))≈ − |
1 |
(b − a)3 f ′′(x ), |
(5.7) |
|
12 |
|||||||
a |
2 |
|
|
|
|
де члени, відкинуті при заміні точної рівності наближеним, містять старші похідні й більше високі ступені довжини відрізка інтегрування. Помітимо, що
утримуючі f (x ) й f ′(x )члени розкладання (5.6) знищилися й не далечіні
внеску в погрішність; це було неважко передбачати, тому що формула трапецій по самому висновку точна для багаточлена першого ступеня.
Це ж можна одержати іншим способом:
Припускаємо, |
що |
|
|
функція |
y = f (x) |
належить |
y C(2) [a,b] |
і двічі |
||||||||||||||||||||||
дифференцируема. |
Будемо |
розглядати |
|
R = R(h) |
як |
функцію |
кроку |
|||||||||||||||||||||||
h = x1 − x0 = b − a . Тоді можна покласти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
R(h)= |
x0 +h |
h |
|
|
|
(x0 )+ y |
(x0 + h) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
∫ |
ydx − |
|
|
|
|
|
(5.8) |
||||||||||||||||
|
|
|
|
|
|
|
2 |
y |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Диференціюємо цю формулу два рази по h. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
′ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
h |
|
′ |
(x0 + h)= |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
R (h)= y(x0 + h)− |
2 |
y(x0 )+ y(x0 + h) − |
2 |
y |
(5.9) |
|||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y(x0 ) |
|
|
|
|
(x0 + h) |
|
|
|
|
||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
y(x0 + h)− |
− |
2 |
y |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R′′(h)= |
1 |
y′(x0 + h)− |
|
1 |
|
y′(x0 + h)− |
h |
|
y′′(x0 + h) |
= − h |
y′′(x0 + h) |
(5.10) |
||||||||||||||||||
|
|
2 |
2 |
|||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
(0)= 0 . |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
причому R(0)= 0 ; |
|
R′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Звідси, інтегруючи |
|
R′′(h) по h й використовуючи теорему про середній, |
||||||||||||||||||||||||||||
одержуємо, послідовно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
R′(h)= R′(0)+ ∫h R′′(t )dt = 0 − |
|
1 |
|
∫h t y′′(x0 + t )dt = − |
|
1 |
y′′(ξ1 )∫h tdt = − h2 |
y′′(ξ1 ), (5.11) |
||||||||||||||||||||||
2 |
|
2 |
||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
4 |
|
|
||||||
40
де ξ1 (x0 , x0 + h)
R(h)= R(0)+ ∫h R′(
0
де ξ (x0 , x0 + h),
, звідси:
t )dt = 0 − 1 ∫h t y′′(x0 + t )dt
4 0
т. е:
R(h)= − 12h3 y′′(ξ )
= − |
1 |
y′′(ξ )∫h t2dt = − h3 |
y′′(ξ ), (5.12) |
||
4 |
|||||
|
0 |
12 |
|
||
|
|
|
|
(5.13) |
|
Знак різниці вказує на те, що якщо друга похідна на відрізку позитивна, то формула (5.5) апроксимується з надлишком, у противному випадку - з недоліком.
Загальна формула трапецій
Взагалі, довжина відрізка b − a не малий, тому залишковий член (5.7) може бути великий. Для підвищення точності на відрізку [a,b] вводять досить густу сітку a = x0 < x1 < x2 < ...< xn = b (розбивають відрізок на n частин). Інтеграл
розбивають на суму інтегралів по кроках сітки й до кожного кроку застосовують формулу (5.5). Одержують загальну (узагальнену) формулу трапецій:
b |
1 |
n |
|
∫ f (x)dx ≈ |
∑(xi − xi−1 ) ( fi−1 + fi ), |
||
|
|||
a |
2 i=1 |
||
(5.14)
R ≈ − 1 ∑n (xi − xi−1 )3 f ′′(xi )
12 i=1
На рівномірній сітці вона спрощується:
b |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
∫ f (x)dx ≈ h |
|
f0 |
+ |
f1 + |
f2 + ...+ |
fn−1 + |
|
fn |
, |
||
2 |
2 |
||||||||||
a |
|
|
|
|
|
|
|
|
|||
|
|
|
|
(5.15) |
|
|
1 |
n |
1 |
b |
|
R ≈ − |
∑h3 f ′′(xi )≈ − |
h2 ∫ f ′′(x)dx , h = xi − xi−1 = const |
|||
12 |
12 |
||||
|
i=1 |
a |
Приклад розрахунку представлений на рис. 5.2
Формула (5.13) не завжди зручна при обчисленнях, тому в більшості випадків застосовують оцінку погрішності по методу Рунге:1 :
|
R = |
Ih − I2h |
|
(5.16) |
|
||||
3 |
|
|
||
Де Ih й I2h - значення інтеграла обчислені на сітці |
з одинарним і |
|||
подвійним кроком розбивки відповідно. |
|
|||
|
|
|
||
1 Вывод данной формулы выносится на самостоятельное изучение. |
|
|||
41
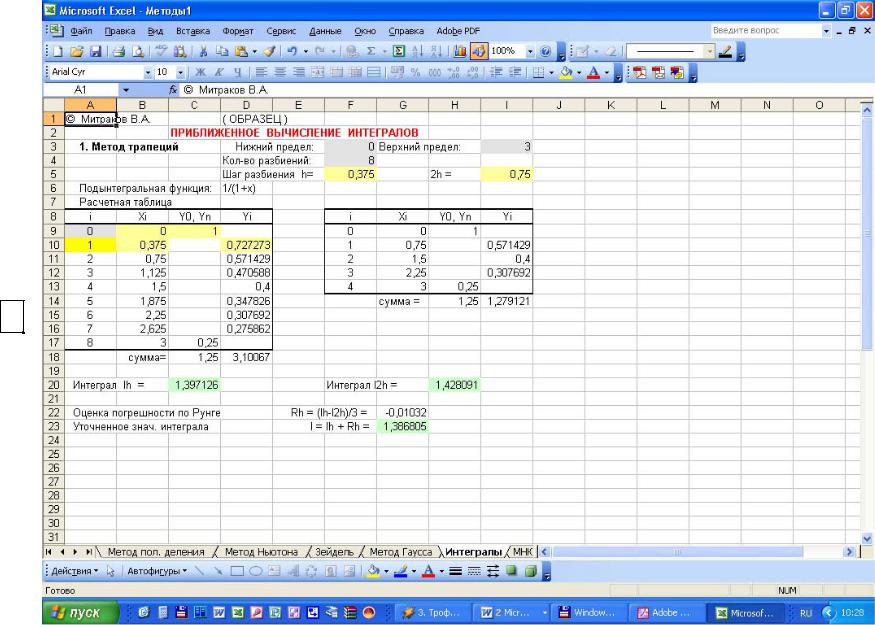
42
Рис. 5.2
Приклад розрахунку по методу трапецій в
Microsoft Excel