Помилка ділення на нуль.

Очевидною пасткою в методі Ньютона є можливість ділення на нуль у формулі (4.3), що виникає, якщо f ' (x(k ) )= 0 . Цілком імовірно, що f (x(k ) )

досить близько до нуля й x(k ) прийнятне наближення до кореня. Розглянемо дану ситуацію й визначимо швидкість збіжності ітерації.

Визначення (порядок кореня): Припустимо, що функція f (x) і її похідні f ' (x),..., f (M ) (x) визначені й безперервні на інтервалі в околиці крапки

f ' (−2)= 9 , так, що M = 1 відповідно до (4.9), тому x* = −2 – простий корінь.

Розглянемо наступні властивості збіжності. Якщо x* - простий корінь рівняння f (x)= 0 , то метод Ньютона сходиться швидко й кількість десяткових

знаків точності приблизно подвоюється з кожною ітерацією. З іншого боку, якщо x* є кратним коренем, то помилка в кожному наступному наближенні

дорівнює частини попередньої помилки. Відзначимо, що метод Ньютона характеризується другим порядком збіжності поблизу кореня й першим порядком - удалині від нього.

1 Вспомогательное предложение, употребляемое при доказательстве одной или нескольких теорем.

33

Модифікації методу Ньютона.

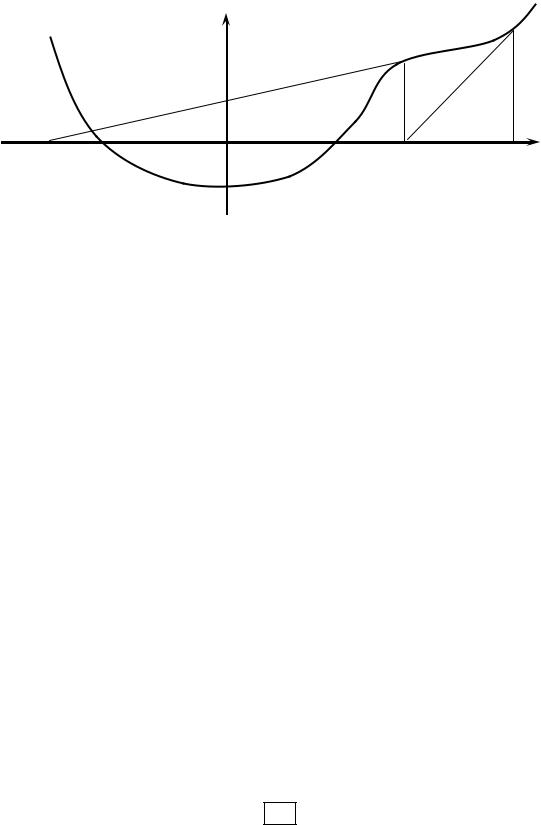
Метод дотичних, будучи досить ефективним засобом чисельного аналізу, на жаль, має досить тверді обмеження. Дійсно, він не може застосовуватися для сіткових рівнянь; при порушенні знакопостоянства похідних (рис. 4.3); при існуванні необмежених других похідних і ін. Так, якщо навіть умова

знакопостоянства порушена вдалині від кореня, де обрано x(0) , а поблизу кореня виконується, то однаково метод дотичних не застосуємо (рис. 4.3), якщо не зробити звуження початкового відрізка.

y

y = f (x)

Рис. 4.3 Приклад незастосовності методу дотичних

Крім цього, у випадку, якщо функція f (x) досить складна, то буде

складної і її похідна, і тому на кожній ітерації доводиться розраховувати дві функції, що знижує ефективність методу дотичних.

У силу цього в ряді випадків можуть виявитися більше кращими модифікації методу дотичних. Розглянемо основні з них:

Спрощений метод Ньютона

Методика його застосування збігається з викладеної для методу Ньютона,

Відмінність від методу Ньютона полягає в тому, що похідна функції f (x)

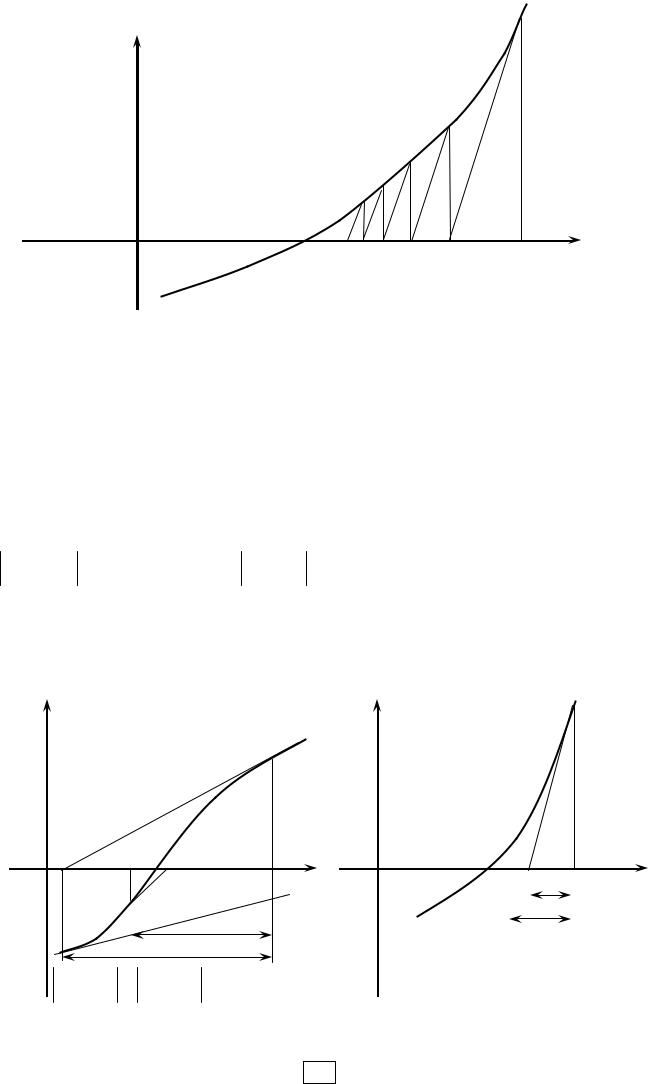
підраховується тільки в крапці початкового наближення, а на наступних ітераціях не уточнюється. Процес послідовних наближень відбитий на рис. 4.4. Перша ітерація збігається з першою ітерацією методу Ньютона. На наступних ітераціях відповідні відрізки паралельні дотичній, проведеної в початковій крапці.

Для цієї модифікації знімаються деякі обмеження методу дотичних, наприклад умова знакопостоянства похідних. Збіжність спрощеного методу Ньютона лінійна.

34

y

y = f (x)

Рис. 4.4 Геометричні побудови для спрощеного методу Ньютона

Метод Ньютона-Бройдена

Цей метод дозволяє збільшити швидкість збіжності послідовних

де ck - число, що вибирається на кожній ітерації так, щоб зменшити значення f (x(k+1) ) в порівнянні с. f (x(k ) ) При ck = 1 метод Ньютона-Бройдена

збігається з методом Ньютона.

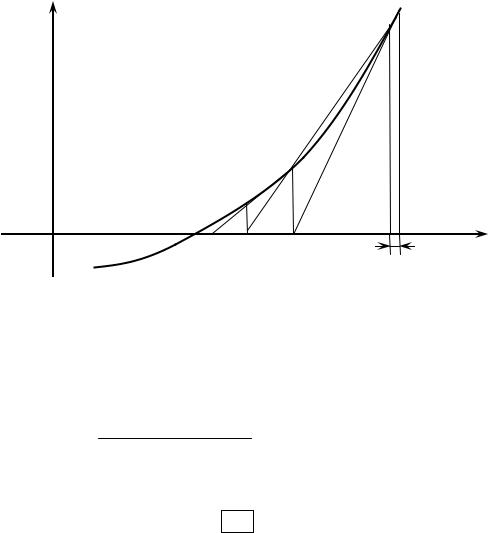
Як правило, при поганій збіжності або її відсутності думають 0 < ck < 1 (рис. 4.5,а), а при гарній збіжності для ck = 1 думають ck > 1 (це прискорює збіжність (рис. 4.5, б)).

f (x(1) ) > f (x(0) )

Рис. 4.5 Геометричні побудови для методу Ньютона-Бройдена

35

y

Методика застосування методу січних збігається з методикою застосування методу Ньютона, але замість (4.3) використається формула:

x(k+1) = x(k ) − f (x(k )f)(−x(fk )()x(k−1) ) (x(k ) − x(k−1) ), k = 1,2,... (4.13)

36

Зауваження:

1.Метод січних є більше економічним у порівнянні з методом Ньютона по

кількості функцій, що підлягають розрахунку: на кожній ітерації в методі січних необхідно розрахувати тільки значення f (x(k ) ), тому що величина

f(x(k−1) ) вже підрахована на попередній ітерації.

2.Для всіх описаних модифікацій швидкість збіжності p в порівнянні з методом дотичних знижується: p < 2 . Однак для деяких з них (метод січних) значення p > 1 й може досягати p = 1,5 .

37