
- •Список прийнятих скорочень
- •Тема 1. Методи розв'язання систем лінійних рівнянь
- •Лекція 1. Метод Гауса
- •Концепція методів
- •Метод Гауса
- •Верхня трикутна система лінійних рівнянь
- •Метод виключення Гауса й вибір головного елемента
- •Схема єдиного ділення
- •Лекція 2. Ітераційні методи
- •Метод ітерацій
- •Зауваження про точність розрахунку
- •Достатня умова
- •Приведення лінійної системи до виду зручному для ітерації.
- •Метод Зейделя
- •Тема 2. Методи рішення нелінійних рівнянь
- •Лекція 3. Метод половинного ділення
- •Наближене рішення нелінійних рівнянь
- •Відділення корінь
- •Метод половинного ділення
- •Лекція 4. Метод Ньютона
- •Методика рішення задачі
- •Помилка ділення на нуль.
- •Швидкість збіжності.
- •Модифікації методу Ньютона.
- •Спрощений метод Ньютона
- •Метод Ньютона-Бройдена
- •Метод січних
- •Тема 3. Чисельне інтегрування
- •Лекція 5. Метод трапецій
- •Постановка задачі
- •Формула трапецій
- •Погрішність формули трапецій
- •Загальна формула трапецій
- •Лекція 6. Метод Сімпсона
- •Формула Сімпсона
- •Залишковий член формули Сімпсона
- •Загальна (узагальнена) формула Сімпсона
- •Тема 4. Обробка експериментальних даних
- •Лекція 7. Інтерполяція
- •Постановка задачі
- •Линейная інтерполяція
- •Квадратична інтерполяція
- •Інтерполяційна формула Лагранжа.
- •Обчислення Лагранжевых коефіцієнтів
- •Інтерполяція сплайном
- •Лекція 8. Метод найменших квадратів
- •Постановка задачі
- •Метод найменших квадратів
- •Лінійна апроксимація (інтерполяція)
- •Коефіцієнт лінійної кореляції
- •Квадратична апроксимація
- •Додатка
- •Транспонування
- •Обчислення визначника матриці
- •Знаходження зворотної матриці
- •Додавання й вирахування матриць
- •Множення матриці на число
- •Множення матриць
- •Ітераційні методи рішення рівнянь
- •Стандартні форми рівнянь
- •Пошук корінь графічним методом
- •Простий ітераційний метод здогаду й перевірки
- •Подання рівняння у формі 2
- •Пряма підстановка
- •Ітерації в осередку
- •Введення в надбудову Пошук рішення
- •Активування надбудови Пошук рішення
- •Установка надбудови Пошук рішення
- •Застосування надбудови Пошук рішення
- •Додаток 3. Контрольні питання
- •Додаток 4. Список лабораторних робіт
- •Частина 1. Обчислювальна техніка
- •Частина 2. Чисельні методи
- •Список літератури.
- •Основна література
- •Додаткова література
- •Інтернет-ресурси
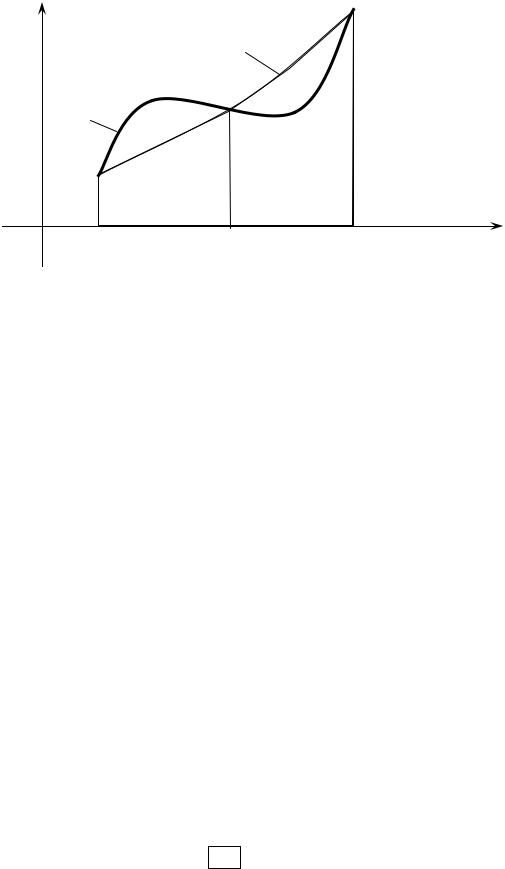
Лекція 6. Метод Сімпсона
Геометрично формула Сімпсона виходить у результаті заміни подінтегральної функції y = f (x) параболою y = L2 (x), що проходить через
три крапки M0 (x0 , y0 ), M1 (x1 , y1 ) і M2 (x2 , y2 ) (рис. 6.1).
M2 (x2 , y2 )
L2 (x)
M1 (x1 , y1 )
f (x)
M0 (x0 , y0 )
Рис. 6.1 Геометричні побудови для методу Сімпсона
Формула Сімпсона
З виду залишкового члена (5.15) треба, що результат, отриманий по формулі трапецій, можна уточнювати методом Рунге. Проводячи таке
уточнення для |
|
відрізка, |
що |
містить |
вузли |
x0 , |
x1 , x2 , |
одержимо |
формулу |
||||||||||||||
Сімпсона. |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ≈ |
|
|
4 F (h)− F (2 h) |
= |
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
трап |
|
трап |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
||
= |
|
|
|
4 h |
|
f0 |
+ f1 + |
|
|
f2 |
|
− 2 |
h |
|
|
f0 |
+ |
|
f |
2 |
|
= |
(6.1) |
3 |
|
|
2 |
|
2 |
2 |
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
1 |
|
h ( f0 + 4 f1 + f2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де h = xi − xi−1 .
Залишковий член формули Сімпсона
Таким чином, залишковий член формули Сімпсона дорівнює:
x
R = ∫2 ydx − h (y0 + 4 y1 + y2 ), де y = f (x) (6.2)
x0 3
43

Припускаємо, що функція y C(4) [a,b], одержимо більше просте вираження й для формули Сімпсона. Фіксуємо середню крапку x1 й розглядаючи R = R(h), будемо мати:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 +h |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= ∫ ydx |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.3) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
y(x1 − h)+ 4 y(x1 )+ y(x1 + h) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 −h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = R(h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Звідси, |
|
диференціюючи функцію |
|
по h послідовно трьох разу, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
одержимо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
R |
(h)= y(x1 + h) |
+ y(x1 − h) |
|
3 |
y(x1 − h)+ 4 y(x1 )+ y(x1 + h) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||
|
|
|
− |
|
|
|
|
|
′ |
(x1 |
|
′ |
(x1 |
|
|
|
|
|
= |
|
|
|
|
|
|
(x1 + h) |
|
|
|
|
|
|
|
|
− |
y(x1 )− |
(6.4) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
−y |
|
− h)+ y |
+ h) |
3 |
|
|
y |
+ y(x1 − h) |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
− |
h |
|
|
|
|
|
′ |
(x1 |
|
′ |
(x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
3 |
|
|
−y |
|
− h)+ y |
+ h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
′′ |
(h)= |
|
|
|
|
|
|
′ |
(x1 − h)+ |
|
|
|
′ |
(x1 + h) |
|
|
|
|
|
|
|
|
|
|
|
′ |
(x1 |
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
||||||||||||||||||||||||||||||||||||
|
R |
3 |
|
−y |
|
y |
|
3 |
|
|
−y |
− h)+ y |
|
(x1 + h) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
− |
h |
|
|
′′ |
(x1 − h)+ y |
′′ |
(x1 |
|
|
|
|
= |
1 |
|
|
|
|
|
′ |
(x1 − h)+ |
|
′ |
|
|
|
|
|
|
|
|
(6.5) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
y |
|
|
|
|
+ h) |
3 |
|
−y |
|
y |
(x1 + h) − |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
− |
h |
|
|
′′ |
(x1 − h)+ y |
′′ |
(x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
3 |
|
y |
|
|
|
|
+ h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
′′′ |
|
|
|
|
|
|
′′ |
(x1 |
− h)+ y |
′′ |
(x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
(x1 − h)+ y |
′′ |
(x1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
(h)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
R |
|
3 |
|
y |
|
|
|
|
|
|
+ h) − |
3 |
|
|
y |
|
|
|
+ h) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
− |
h |
|
−y |
′′′ |
(x1 − h)+ y |
′′′ |
(x1 |
|
|
|
|
= − |
|
h |
|
|
|
′′′ |
(x1 |
− h) |
+ y |
′′′ |
(x1 |
|
+ h) |
|
= |
(6.6) |
||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
+ h) |
|
3 |
− y |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= − |
|
h2 yIV (ξ3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де ξ3 (x1 − h, x1 + h). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Крім того, |
маємо R(0)= 0 ; R′(0)= 0 ; |
|
R′′(0)= 0 . Послідовно інтегруючи |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
R′′′(h) й використовуючи теорему про середній, знаходимо: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R′′(h)= R′′(0)+ ∫h R′′′(t )dt = − |
2 |
|
∫h t 2 yIV (ξ3 )dt = − |
|
2 |
yIV (ξ2 )∫h t2dt = − |
2 |
h2 yIV (ξ2 ) |
(6.7) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
3 |
9 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
де ξ2 (x1 − h, x1 + h). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
R′(h)= R′(0)+ ∫h R′′(t )dt = − |
|
2 |
|
∫h t3 yIV (ξ2 )dt = − |
|
2 |
yIV |
(ξ1 )∫h t 3dt = − |
|
1 |
|
h4 yIV (ξ1 ) |
(6.8) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 |
|
9 |
18 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
де ξ1 (x1 − h, x1 + h). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
R(h)= R(0)+ ∫h R′(t )dt = − |
|
1 |
|
∫h t4 yIV (ξ1 )dt = − |
1 |
|
|
yIV (ξ )∫h t4dt = − |
|
1 |
|
h5 yIV (ξ ) |
(6.9) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
18 |
|
18 |
|
90 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
44

де ξ (x1 − h, x1 + h).
Таким чином, залишковий член формули Сімпсона дорівнює:
R = − |
h5 |
yIV (ξ ), де ξ (x0 , x2 ) |
(6.10) |
|
|||
90 |
|
|
|
Т.о. формула Сімпсона більше точна, чим формула трапецій.
Загальна (узагальнена) формула Сімпсона
|
|
Нехай |
|
n = 2 m є |
|
парне |
число й |
yi = f (xi ) |
(i = 0,1,2,...,n) |
значення |
|||||||||||||||
функції |
|
y = f (x) |
для рівновіддалених крапок |
a = x0 < x1 < x2 < ...< xn = b із |
|||||||||||||||||||||
кроком h = b − a = b − a . |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
2 m |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Застосовуючи |
|
формулу |
Сімпсона |
до |
кожного |
подвоєного |
проміжку |
||||||||||||||||
x |
, x |
2 |
|
, x |
2 |
, x |
|
|
... x |
2 m− |
2 |
, x |
довжини 2 h одержимо: |
|
|
|
|||||||||
|
0 |
|
|
|
|
|
4 |
|
|
|
2 m |
|
|
|
|
|
|
|
|
||||||
∫b |
ydx ≈ h |
(y0 + 4 y1 + y2 ) |
+ h (y2 + 4 y3 + y4 )+ ...+ h |
(y2 m−2 + 4 y2 m−1 + y2 m ) |
|||||||||||||||||||||
a |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
b |
|
Звідси одержуємо загальну (узагальнену) формулу Сімпсона: |
|
|
|||||||||||||||||||||
|
|
|
|
h |
|
|
|
|
|
+ y2 m )+ 4 (y1 + y3 + ...+ |
y2 m−1 )+ |
|
|
|
|
|
|||||||||
∫ ydx ≈ |
|
|
|
|
|
|
|
|
|
(6.11) |
|||||||||||||||
3 |
(y0 |
|
2 (y2 + y4 + ...+ y2 m−2 ) |
||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Або: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
b |
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
2 m−1 |
|
2 m− |
2 |
|
|
|
|
|
|
|
∫ ydx ≈ |
|
|
|
+ y2 m )+ 4 ∑ yi нечёт. |
+ 2 |
|
|
|
|
|
|||||||||||||
|
|
3 |
|
(y0 |
∑ yi чёт. |
|
(6.12) |
||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
i=2 |
|
|
|
|
|
||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 m−1 |
|
|
|
1, |
при i − нечёт. |
|
|
||||
∫ ydx ≈ h |
|
|
|
+ y2 m )+ ∑ (3 |
|
|
(6.13) |
||||||||||||||||||
(y0 |
+ Ci ) yi , де C = |
|
при i − чёт. |
||||||||||||||||||||||
a |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
−1, |
|
|
||||
Залишковий член загальної формули Сімпсона дорівнює сумі залишкових членів на кожній з m ділянок. Якщо ввести середнє значення четвертої похідної yc IV (ξ ), то:
R = − |
h5 |
yc IV (ξ )= −(b − a) |
h4 |
yc IV (ξ ) |
(6.14) |
|
180 |
||||
90 |
|
|
|
||
Частіше цю формулу не застосовують, а виконують прорахунок із кроком h і 2 h . Одержуємо:
R = −(b − a) |
h4 |
|
yIV |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
h |
|
|
180 |
|
|
|
R2h |
= 16 |
|
|
|
|
(6.15) |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
(2 |
h)4 |
|
|
|
|
|
|
||||
R |
= −(b − a) |
|
yIV |
|
Rh |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
2h |
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
||
I = Ih + Rh |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ih + Rh = I |
2h + 16 Rh Rh = |
I |
h |
− I |
2h |
(6.16) |
||||||||||
|
|
|
|
|||||||||||||
I = |
|
|
15 |
|
||||||||||||
I2h + R2h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Формула (6.16) - перевірка погрішності по Рунге. Приклад розрахунку представлений на рис. 6.2
45

Рис. 6.2
Приклад
розрахунку по методу Сімпсона в
Microsoft Excel
46
