a0 |
= A−1 B |
(8.13) |
a1 |
|
|
Знайдені параметри регресії a0 , a1 підставляють у рівняння (8.8) і в такий
спосіб одержують емпіричне лінійне рівняння щонайкраще описує експериментальні дані.
Коефіцієнт лінійної кореляції1
Для оцінки відповідності підібраної прямої й експериментальних даних уводять поняття коефіцієнта лінійної кореляції, що обчислюється по формулі:
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
∑(xk − |
|
) (yk − |
|
) |
|
|
||||
|
|
|
|
|
|
|
Ryx |
|
x |
y |
||||||||||
|
|
|
|
|
|
|
= |
k=1 |
|
|
|
|
|
(8.14) |
||||||
|
|
|
|
|
|
|
N |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
||||||||||
|
|
|
|
|
|
|
|
|
|
∑(xk − |
|
)2 |
∑(yk − |
|
)2 |
|
||||
|
|
|
|
|
|
|
|
|
|
x |
y |
|||||||||
|
|
|
|
|
|
|
|
|
|
k=1 |
k=1 |
|||||||||
де: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
N |
1 |
|
N |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= |
∑xk , |
|
= |
|
∑yk – середні величини змінних х и в. |
|||||||||||||
|
x |
y |
||||||||||||||||||
|
N |
|
||||||||||||||||||
|
|
|
k=1 |
N |
k=1 |
|
|
|
|
|
|
|
|
|
|
|
||||
Коефіцієнт кореляції характеризує тісноту лінійної залежності й приймає |
||||||||||||||||||||
значення в інтервалі |
−1 ≤ Ryx ≤ 1. Чим ближче Ryx до 1 або -1, тих тесней |
|||||||||||||||||||
лінійний зв'язок (пряма або зворотна) між змінними х и в.
Квадратична апроксимація
При m = 2 одержуємо функцію:
f(x)= a0 + a1 x + a2 x2
Уцьому випадку нормальна система має вигляд:
|
∂F (a0 , a1 ,a2 ) |
N |
||||||
|
= 2∑(a0 + a1 xk + a2 xk 2 − yk )= 0 |
|||||||
∂a0 |
|
|
|
|
||||
|
|
|
|
|
k=1 |
|||
|
∂F (a , a |
|
,a |
|
) |
N |
||
|
1 |
2 |
= 2∑(a0 + a1 xk + a2 xk 2 − yk ) xk = 0 |
|||||
|
0 |
|
|
|
||||
∂a1 |
|
|
|
|
||||
|
|
|
|
|
k=1 |
|||
|
∂F (a0 , a1 ,a2 ) |
N |
||||||
|
= 2∑(a0 + a1 xk + a2 xk 2 − yk ) xk 2 = 0 |
|||||||
∂a |
|
|
|
|
|
|||
|
2 |
|
|
|
|
k=1 |
||
|
|
|
|
|
|
|
||
(8.15)
(8.16)
Після перетворення маємо нормальну систему трьох рівнянь щодо невідомих параметрів регресії a0 , a1 , a2 .
1 Данный раздел предназначен для самостоятельного изучения
55
|
|
N |
N |
N |
|
a0 N + a1 ∑xk + a2 ∑xk2 = |
∑yk |
|
|||
|
|
k=1 |
k=1 |
k=1 |
|
|
N |
N |
N |
N |
|
a0 |
∑xk |
+ a1 ∑xk2 + a2 ∑xk3 = ∑xk yk |
(8.17) |
||
|
k=1 |
k=1 |
k=1 |
k=1 |
|
|
N |
N |
N |
N |
|
a0 |
∑xk2 + a1 ∑xk3 + a2 ∑xk4 = ∑xk2 yk |
|
|||
|
k=1 |
k=1 |
k=1 |
k=1 |
|
Вирішивши систему (8.17) щодо параметрів a0 , a1 , a2 одержуємо
конкретний вид функції (8.15). Зміна кількості параметрів не приведе до зміни суті самого підходу, а виразиться в зміні кількості рівнянь у системі (8.17).
Значення разностей |
|
yk − F (a0 ,a1 ,a2 )= εk |
(8.18) |
називають відхиленнями обмірюваних значень від обчислених по формулах
(8.8) або (8.15).
Сума квадратів відхилень
N |
|
|
σ = ∑εk2 |
(8.19) |
|
k= |
1 |
|
відповідно до принципу найменших квадратів для заданого виду функції, що наближає, повинна бути найменшої.
Із двох різних наближень однієї й тієї ж табличної функції кращим уважається те, для якого (8.19) має найменше значення.
Аналогічно можна записати систему для полінома будь-якого ступеня m ≤ N :
f (x)= a0 + a1 x + a2 x2 + ...+ am xm |
(8.20) |
При цьому, якщо m = N , те крапкова середня квадратична апроксимація алгебраїчним багаточленом збігається з лагранжевой інтерполяцією. Отже, підвищення ступеня апроксимуючого полінома на певному кроці приведе до погіршення якості й викличе необхідність використати апроксимацію сплайнами. Інший шлях підвищення якості апроксимації пов'язаний з вибором замість алгебраїчних поліномів інших ортогональних поліномів, а також функцій виду:
y = a xb |
y = a bx |
y = a + |
b |
|
|||
x |
|||||||
|
|
|
|
|
|||
|
1 |
|
x |
|
(8.21) |
||
y = |
y = |
y = a lg x |
|||||
a x + b |
a x + b |
||||||
|
|
|
|
|
|||
і інших, які легко линеаризуются шляхом логарифмування або заміни змінних.
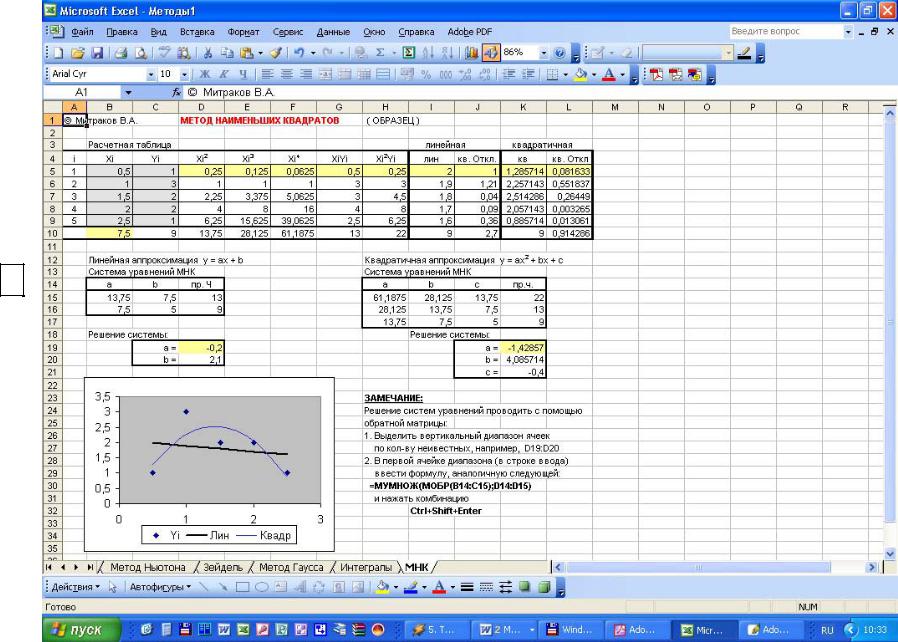
Приклад реалізації методу найменших квадратів у середовищі Microsoft Excel представлений на рис. 8.2.
56
57
Рис. 8.2
Приклад
розрахунку по методу найменших квадратів в
Microsoft Excel