Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасская национальная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

КЛ по ВТиП-часть2_укр.pdf

Скачиваний:

Добавлен:

21.02.2016

Размер:

3.34 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2111 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Тема 4. Обробка експериментальних даних

Лекція 7. Інтерполяція1

Найпростіше завдання інтерполяції полягає от у чому. Нехай на деякому відрізку [a,b] задані n + 1 крапки x0 , x1 ,..., xn , які називаються вузлами

інтерполяції, і значення функції f (x) в цих крапках

Потрібно побудувати функцію F (x) (интерполирующая функція), принадлежащею певному класу й приймаючу у вузлах інтерполяції ті ж значення, що й f (x), тобто F (x0 )= y0 , F (x1 )= y1 , F (xn )= yn .

Геометрично це означає, що потрібно знайти криву y = F (x) певного

типу, що проходить через задані крапки.
У	такій постановці задача або має незліченну множину рішень або не
одного.		Fn (x) ступеня n, то
Якщо ж функцію F шукати у вигляді полінома
задача	стає однозначною. Отриману інтерполяційну	формулу y = F (x)

звичайно використають для наближеного обчислення значень даної функції f (x) при значеннях аргументу x , відмінних від вузлів інтерполяції. Така

операція називається інтерполяцією функції f (x). Більш точно, розрізняють інтерполяція у вузькому змісті, коли x x0 , xn й екстраполювання, коли x x0 , xn . Ми будемо й першу й другу операцію розуміти як інтерполяція.

Постановка задачі

Деяка функція		y = f (x) задана		таблицею	своїх	значень на множині
равностоящих значень аргументу x .
	x		x1	x2	…	xn
	y		y1	y2	…	yn

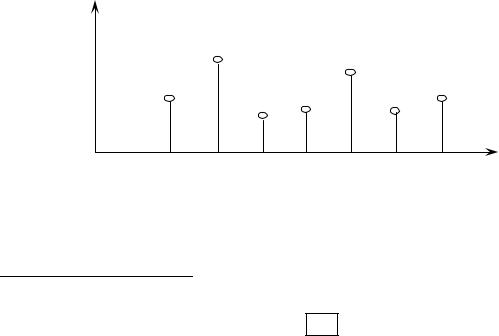
На графіку це виглядає в такий спосіб (рис. 7.1):

		y2
	y1		yn
	x1	x2	xn
Рис. 7.1	Значення функції		y = f (x) на множині равностоящих

значень аргументу x

1 Данная тема предназначена для самостоятельного изучения

Щоб знайти значення функції при будь-якім значенні аргументу x , необхідно побудувати аналітичну функцію F (x), що збігалася б з невідомою

функцією f (x) у вузлах таблиці й наближалася б до неї поза вузлами. Тим самим, буде, як би відновлена невідома функція f (x) замінена тепер на відому

– F (x). Ступінь погрішності інтерполяції, тобто різниця f (x)− F (x) при заданому значенні x залежить від ширини інтервалу h = xi+1 − xi й від виду функції, що інтерполює.

Линейная інтерполяція

Значення функції поза вузлами таблиці найпростіше обчислити, заміняючи невідому функцію на кожному відрізку [xi , xi+1 ] лінійною функцією

	F1 (x)= b0 + b1 x ,			(7.1)
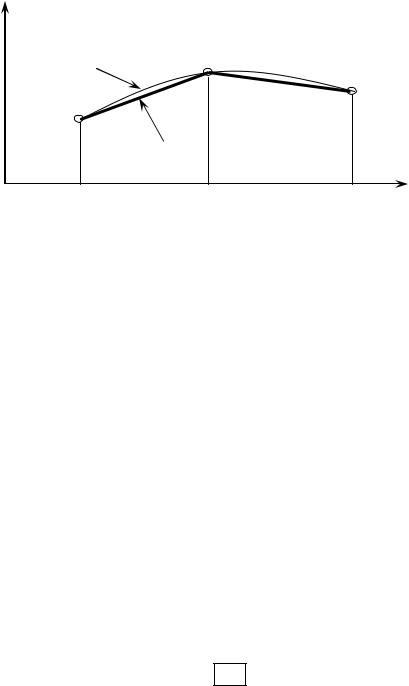
т.е. відрізком прямої, що з'єднує вузлові крапки таблиці (рис. 7.2).
y
	f(x)	y2
	y1
		F(x)
	x1	x2	x
			x
Рис. 7.2	Графічне подання лінійної інтерполяції
Невідомі коефіцієнти b0 , b1 визначаються з рішення системи рівнянь,
отриманої із припущення,		що значення невідомої функції		f (x) й значення
функції F1 (x)	збігаються у вузлах x1 і x2 .

Квадратична інтерполяція

Лінійна інтерполяція, як це видно з рис. 7.2, має більшу погрішність. Щоб зменшити погрішність, невідому функцію f (x) інтерполюють поліномом другого ступеня.

F2 (x)= b0 + b1 x + b2 x2

(7.2)

Т. е. через три крапки (y1 , x1 ); (y2 , x2 ); (y3 , x3 ) проводять параболу (7.2). Значення коефіцієнтів b0 , b1 , b2 знаходять вирішуючи систему трьох рівнянь,

отриманих із припущення, що значення невідомої функції f (x) й значення полінома F2 (x) збігаються у вузлах x1 , x2 , x3 .

Інтерполяційний поліном кожної n-ой ступеня можна побудувати, маючи n + 1 вузол таблично заданої функції. Ці поліноми Fn (x) називаються

інтерполяційними поліномами Лагранжа.

Поліноми Лагранжа дають гарна якість інтерполяції при великій кількості вузлів і високого ступеня полінома. Однак у поліномів Лагранжа є два важливих недоліки:

9Існують функції, при інтерполяції яких, збільшення ступеня полінома не дає гарного наближення.

9Інтерполяційні поліноми Лагранжа у вузлах з'єднання мають злами.

Це вкрай небажане явище, тому що виникають труднощі з диференціюванням

іінтегруванням такої функції.

Інтерполяційна формула Лагранжа.

Лагранжем уведена формула для інтерполяції, що є більше загальної, тому що вона застосовна для випадку довільного розташування вузлів інтерполяції

(нерівномірно розташованих)

Нехай на відрізку [a,b]

дані n + 1 різних значень аргументу x0 , x1 ,..., xn й

відомі відповідні значення функції

f (x);

f (x0 )= y0 , f (x1 )= y1 ,…, f (xn )= yn

Потрібно побудувати поліном Fn (x) ступеня не вище n, що має в заданих

вузлах x0 ,x1 ,..., xn ті ж значення,

що

й функція

f (x),

тобто

Fn (x0 )= y0 ,

Fn (x1 )= y1 ,…, Fn (xn )= yn ...

1) Спочатку вирішимо таку задачу: побудувати поліном Pi (x)

такий, що

Pi (x j )= 0 при

j ≠ i й Pi (xi )= 1, тобто це можна записати так:

Pi (x j )

=δij

(символ Кронекера)

Тому

що

вихідний

поліном

звертається

в 0

крапках:

x0 ,x1 ,..., xi−1 ,xi+1 ,..., xn , те він має вигляд:

Pi (x)= Ci (x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )

(7.3)

де Ci

– постійний коефіцієнт; не залежний від x .

Ci знайдемо з (7.3) поклавши x = xi

й з огляду на, що Pi (xi )= 1, тобто

Ci (xi − x0 ) (xi − x1 ) ... (xi − xi−1 ) (xi − xi+1 ) ... (xi − xn )= 1

= 1

((xi − x0 ) (xi

− x1 ) ... (xi − xi−1 ) (xi − xi+1 ) ... (xi − xn ))

Підставивши це в (7.3), одержимо:

(x)=

(x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )

((xi − x0 ) (xi

− x1 ) ... (xi − xi−1 ) (xi

− xi+1 ) ... (xi

− xn ))

Т.е. задача перша вирішена.

2) Тепер вирішимо більше загальну задачу відшукання Fn (x)

Цей поліном має вигляд:

	n
Fn (x)= ∑Pi (x) yi
	i=0
Справді, ступінь його не вище n й він приймає значення						yi в крапках
x = xi . Т.е. шуканий поліном має вигляд:
n			(x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )
Fn (x)= ∑yi							(7.4)
Fn (x)= ∑yi		((xi − x0 ) (xi − x1 ) ... (xi		− xi−1 ) (xi	− xi+1 ) ... (xi	− xn ))	(7.4)
i=0		((xi − x0 ) (xi − x1 ) ... (xi		− xi−1 ) (xi	− xi+1 ) ... (xi	− xn ))
Це – інтерполяційна формула Лагранжа
Обчислення Лагранжевых коефіцієнтів
Якщо формулу (7.4) записати у вигляді:
	n
Fn (x)= ∑Fi(n) (x) yi , те
F (n) (x)=i=			0 (x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )				(7.5)
F (n) (x)=i=							(7.5)
i			((xi − x0 ) (xi − x1 ) ... (xi	− xi−1 ) (xi	− xi+1 ) ... (xi	− xn ))
			((xi − x0 ) (xi − x1 ) ... (xi	− xi−1 ) (xi	− xi+1 ) ... (xi	− xn ))

називають Лагранжевыми коефіцієнтами.

У випадку постійного кроку h існують таблиці для Лагранжевых коефіцієнтів і обчислювати їх не треба.

Інтерполяція сплайном

Для проведення гладкої кривої через вузлові крапки (y1 , x1 ); (y2 , x2 ); … (yn , xn ) звичайно використають гнучку сталеву лінійку. Її ставлять на ребро й

закріплюють у вузлах. Вісь лінійки описує при цьому гладку криву, що і буде інтерполювати задану таблицею функцію. Отримана в такий спосіб інтерполяційна функція називається сплайном. Сплайн функція не має недоліків поліномів Лагранжа. У неї немає зламів, і гнучка крива легко приймає на одній ділянці вид прямій, а на сусідньому вид параболи.

Чисельні значення коефіцієнтів сплайн поліномів визначають із наступних умов:

9Значення полінома дорівнює значенню шуканої функції у вузлах

таблиці.

91-я й 2-я похідні сплайн поліномів ліворуч і праворуч від будьякого вузла таблиці рівні один одному. Це означає, що сплайн функція не має у вузлах таблиці не тільки зламів, але й зміни радіусів кривизни.