
- •Список прийнятих скорочень
- •Тема 1. Методи розв'язання систем лінійних рівнянь
- •Лекція 1. Метод Гауса
- •Концепція методів
- •Метод Гауса
- •Верхня трикутна система лінійних рівнянь
- •Метод виключення Гауса й вибір головного елемента
- •Схема єдиного ділення
- •Лекція 2. Ітераційні методи
- •Метод ітерацій
- •Зауваження про точність розрахунку
- •Достатня умова
- •Приведення лінійної системи до виду зручному для ітерації.
- •Метод Зейделя
- •Тема 2. Методи рішення нелінійних рівнянь
- •Лекція 3. Метод половинного ділення
- •Наближене рішення нелінійних рівнянь
- •Відділення корінь
- •Метод половинного ділення
- •Лекція 4. Метод Ньютона
- •Методика рішення задачі
- •Помилка ділення на нуль.
- •Швидкість збіжності.
- •Модифікації методу Ньютона.
- •Спрощений метод Ньютона
- •Метод Ньютона-Бройдена
- •Метод січних
- •Тема 3. Чисельне інтегрування
- •Лекція 5. Метод трапецій
- •Постановка задачі
- •Формула трапецій
- •Погрішність формули трапецій
- •Загальна формула трапецій
- •Лекція 6. Метод Сімпсона
- •Формула Сімпсона
- •Залишковий член формули Сімпсона
- •Загальна (узагальнена) формула Сімпсона
- •Тема 4. Обробка експериментальних даних
- •Лекція 7. Інтерполяція
- •Постановка задачі
- •Линейная інтерполяція
- •Квадратична інтерполяція
- •Інтерполяційна формула Лагранжа.
- •Обчислення Лагранжевых коефіцієнтів
- •Інтерполяція сплайном
- •Лекція 8. Метод найменших квадратів
- •Постановка задачі
- •Метод найменших квадратів
- •Лінійна апроксимація (інтерполяція)
- •Коефіцієнт лінійної кореляції
- •Квадратична апроксимація
- •Додатка
- •Транспонування
- •Обчислення визначника матриці
- •Знаходження зворотної матриці
- •Додавання й вирахування матриць
- •Множення матриці на число
- •Множення матриць
- •Ітераційні методи рішення рівнянь
- •Стандартні форми рівнянь
- •Пошук корінь графічним методом
- •Простий ітераційний метод здогаду й перевірки
- •Подання рівняння у формі 2
- •Пряма підстановка
- •Ітерації в осередку
- •Введення в надбудову Пошук рішення
- •Активування надбудови Пошук рішення
- •Установка надбудови Пошук рішення
- •Застосування надбудови Пошук рішення
- •Додаток 3. Контрольні питання
- •Додаток 4. Список лабораторних робіт
- •Частина 1. Обчислювальна техніка
- •Частина 2. Чисельні методи
- •Список літератури.
- •Основна література
- •Додаткова література
- •Інтернет-ресурси

Тема 2. Методи рішення нелінійних рівнянь1
Лекція 3. Метод половинного ділення
Наближене рішення нелінійних рівнянь
Для досить складних алгебраїчних і трансцендентних рівнянь не завжди можна знайти точне рішення, тому дуже часто доводиться застосовувати наближені (чисельні) методи знаходження корінь таких рівнянь.
Нехай дане нелінійне рівняння
f (x)= 0 |
(3.1) |
Де f (x) – функція певна й безперервна на якімсь (навіть нескінченному) інтервалі a < x < b. У деяких випадках на функцію f (x) можуть бути
накладені додаткові обмеження, наприклад, безперервність першої й другої похідних, що спеціально обмовляється.
Потрібно знайти корінь рівняння (3.1). Т. е. Числаx*1 , x*2 ,..., які шляхом підстановки їх в (3.1) перетворюють рівняння у вірну числову рівність. Числа x*1 , x*2 ,... також називаються нулями функції f (x).
Визначення 1 коренем рівняння (3.1) називається значення x = x* , що обертає функцію f (x) в нуль, тобто f (x* )≡ 0 .
Визначення 2 ізольований корінь – це значення x , що задовольняє (3.1) і не утримуючих інших корінь у своїй околиці.
Умова існування кореня рівняння (3.1) треба з теореми:
Якщо безперервна функція f (x) приймає значення різних знаків на кінцях відрізка [a,b], тобто f (a) f (b)< 0 , то усередині цього відрізка втримується, принаймні, один корінь рівняння f (x)= 0 . Виходить, найдеться хоча б одне число x* (a,b) таке, що f (x* )= 0 . Якщо ж f (x) безперервна й диференцуєма і її перша похідна зберігає знак усередині відрізка [a,b], то на
даному відрізку перебуває тільки один (ізольований) корінь x = x* рівняння.
Таким чином, при знаходженні корінь рівняння (3.1) чисельним методом, крім безперервності f (x) передбачається:
1.Функція приймає на кінцях відрізка різні знаки;
2.Похідні f ' (x) й f "(x) безперервні на відрізку;
3.Похідні на відрізку не міняють знака.
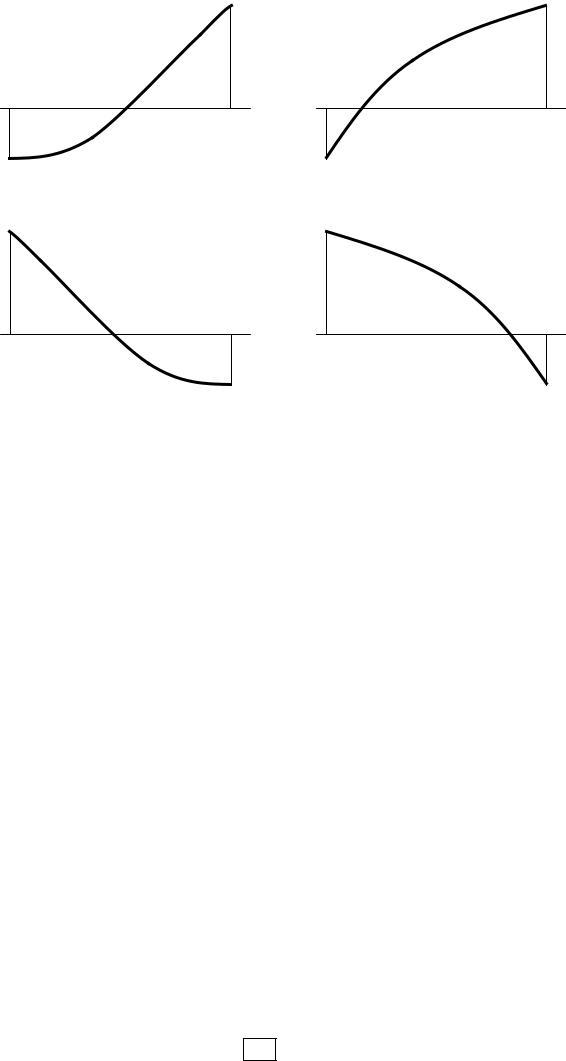
Геометрично остання умова означає, що передбачається одна із чотирьох схем (рис. 3.1).
1 В приложении 2 рассмотрены способы решения уравнений с помощью итерационных методов
23
а |
b |
а |
b |
а |
b |
а |
b |
Рис. 3.1. Геометричне трактування знакопостійності похідних
Наближене знаходження ізольованих дійсних корінь рівняння (3.1) здійснюється у два етапи:
1.Перебувають відрізки ai ,bi , усередині кожного з яких утримується один і тільки один корінь рівняння. Цей етап називається процедурою відділення корінь. По суті, на ньому здійснюється грубе знаходження корінь x = x*i .
2.Грубе значення кожного кореня x = x*i уточнюється до заданої точності
одним із чисельних методів, у яких реалізуються послідовні наближення. Перший етап значно складніше другого. Тому що не існує досить
ефективних методів відділення всіх корінь. Найчастіше використають наступні способи знаходження відрізків ізоляцій: графічний (за допомогою побудови й дослідження графіків функцій); аналітичний (заснований на докладному дослідженні функції); метод послідовного перебору (заснований на обчисленні функції із заданим кроком аргументу й виділенні тих відрізків, де функція міняє знак).
Відділення корінь
Відділення корінь починається із установлення знаків f (x) у граничних
крапках області визначення функції.
Після цього, або аналітично, або графічно, використовуючи особливості функції, знаходять значення функції в деяких проміжних крапках x = x1 , x2 ,... і
вибирають інтервали, у яких функція має різні знаки на кінцях інтервалу. За умовами вищевикладеної теореми в таких інтервалах існує корінь рівняння.
Після цього необхідно переконається в тім, що в кожному інтервалі перебуває тільки один корінь. У противному випадку змінювати інтервал.
24
Зауваження 1: якщо відомі коріння рівняння f ' (x)= 0 , то процес відділення корінь можна спростити. Для цього досить визначити знаки функції f (x) в крапках нулів її похідній f ' (x)= 0 і граничним крапкам визначення функції x = a й x = b .
Зауваження 2: дійсних корінь рівняння f (x)= 0 можна відокремити приблизно, як крапки перетинання графіком y = f (x) осі абсцис.
Цей метод зручний своєю наочністю, але при обчисленнях вручну ним не завжди можна скористатися, оскільки:
1. f (x) являє собою функцію, графік якої побудувати складно (наприклад, y = ex + sin x ).
2. Обмеженість розмірів креслення дозволяє знайти корінь тільки в деякому обмеженому проміжку.
Перший недолік можна усунути, якщо вдається записати вихідне рівняння f (x)= 0 у вигляді ϕ(x)= g(x), при якому y =ϕ(x) й y = g(x) побудувати значно простіше. Тоді корінь рівняння перебувають як абсциси крапок
перетинання графіків |
y =ϕ(x) |
і y = g(x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Приклад 1. Відокремити корінь рівняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x ln x = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рішення. Запишемо це рівняння у вигляді ln x = |
1 |
. Побудуємо графіки й |
|||||||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||||
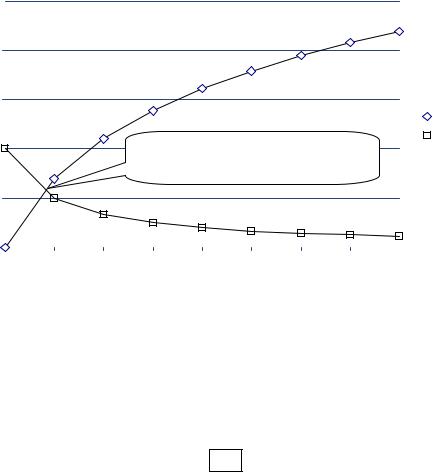
визначимо крапку їхнього перетинання (рис. 3.2). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Точка пересечения – корень |
|
|
|
|
|
|
|
|
|
|
|
1/x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0,5 |
|
|
|
|
|
|
|
|
уравнения x ln x = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|||||||||||||||||
Рис. 3.2. Рішення рівняння x ln x = 1.
Достоїнством графічного методу (крім його наочності) є те, що часто він дає можливість оцінити кількість корінь і їхні знаки.
Перейдемо до другого етапу чисельного рішення рівнянь - уточненню корінь до потрібної точності. На цьому етапі застосовують кілька методів.
25

Метод половинного ділення
Інакше цей метод називають метод Больцано ділення навпіл або метод бісекцій.
Нехай дане рівняння f (x)= 0 , є відрізок [a,b] ізоляції кореня x* для даного рівняння, f (x) безперервна на відрізку [a,b]. Тоді графік функції
y = f (x) перетинає вісь OX на відрізку [a,b] в крапці x* |
й значення функції |
на кінцях відрізка мають різні знаки, тобто |
|
f (a) f (b)< 0 . |
(3.2) |
Відрізок [a,b], у цьому випадку, називається початковим інтервалом
невизначеності, тому що відомо, що корінь йому належить, але його місце розташування з необхідною точністю не визначено.
Основна ідея методу бісекцій: ділимо відрізок ізоляції навпіл і вибираємо ту половину, де функція міняє знак, одержуємо новий відрізок ізоляції, довжина якого у два рази менше попереднього. Цю процедуру повторюємо доти, поки довжина відрізка ізоляції не стане менше заданої точності. Розглянемо це більш докладно.
|
Для знаходження кореня ділимо відрізок [a,b] |
a |
+ b |
||||||||||
|
навпіл. Якщо f |
2 |
= 0 , |
||||||||||
|
|
a + b |
|
|
|
|
|
|
|
|
|||
то |
c = |
|
є коренем. Уважаємо, що f (c)≠ 0 . Тоді виберемо ту з половинок |
||||||||||
|
|||||||||||||
|
|
|
2 |
|
a + b |
a + b |
|
|
|
|
|||
відрізка |
|
|
|
знаки, і |
|||||||||
a; |
2 |
|
або |
2 |
;b , на кінцях якої функція має різні |
||||||||
|
|
|
|
|
|
|
|
|
|
||||
позначимо цей відрізок a1 ;b1 . Довжина цього відрізка: b1 − a1 = b −2 a .
Відрізок a1 ;b1 знову ділимо навпіл і вибираємо новий відрізок a2 ;b2 аналогічно. Будуємо послідовність відрізків an ;bn , кожний з яких удвічі
менше попереднього, таким чином Одержимо послідовність вкладених друг у |
|||||||
друга проміжків a ;b таких, що |
f (a |
) f (b ) |
< 0 (i = 1,2,3,...,n). |
||||
i i |
|
i |
|
|
i |
|
|
Цей процес послідовного ділення навпіл продовжуємо доти, поки не |
|||||||
виконається одне із двох умов: |
|
an + bn |
|
|
|
||
1. Або найдеться така крапка cn |
= |
, |
у |
якій f (cn )= 0 і cn – точне |
|||
|
|||||||
|
|
|
2 |
|
|
|
|
значення кореня (на практиці виходить досить рідко).
2.Або на деякому кроці одержимо відрізок ізоляції an ;bn , довжина якого менше необхідної точності:
b |
− a |
|
= b − a |
< ε |
(3.3) |
n |
|
n |
2n |
|
|
Ліві кінці відрізків утворять монотонну неубутну послідовність an , а праві
– bn , утворять монотонну незростаючу послідовність. Отже, ці послідовності
26

мають той самий межу x* :
x* = lim an = lim bn
n→∞ n→∞
Підставляючи x* в (3.2) перейдемо до межі. Одержимо
lim f (an ) f (bn )= f (x* ) f (x* )< 0 .
n→∞
Це протиріччя, значить f (x* )= 0 .
Тому що корінь належить відрізку ізоляції an ;bn . ТЕ в цьому випадку,
будь-яке число із цього відрізка відрізняється від точного значення кореня менше, ніж на ε . Числа an і bn є наближеними значеннями шуканого кореня з
недоліком і надлишком відповідно. Звичайно беруть як відповідь число із середини останнього відрізка ізоляції:
x* = |
an + bn |
= cn |
(3.4) |
|
|||
2 |
|
|
|
Можна заздалегідь оцінити кількість ділень |
навпіл вихідного відрізка. |
||
Тому що щораз довжина відрізка зменшується у два рази, то по досягненні
необхідної точності |
|
ε |
за n |
кроків |
одержимо відрізок |
довжиною |
||||||||
b − a |
|
= b − a < ε . Звідси можна виразити, прологарифмировав, n: |
|
|||||||||||
n |
n |
2n |
|
|
|
|
b − a |
|
|
|
||||
|
|
|
|
|
|
|
lg |
ε |
|
|
|
|
||
|
|
|
|
|
n > |
|
|
|
|
(3.5) |
||||
Або |
|
|
|
lg 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
lg (b − a) |
|
|
|
|
|
|
|||||
|
|
|
|
|
n > |
− |
lgε |
|
(3.6) |
|||||
|
|
|
|
|
|
lg 2 |
||||||||
|
|
|
|
|
|
|
lg 2 |
|
|
|
||||
Із цієї формули можна оцінити кількість кроків. Крім того, з її видно, що |
||||||||||||||
для того, щоб поліпшити точність у k раз, |
тобто Поклавши ε* = ε |
, необхідно |
||||||||||||
|
|
|
|
lg k |
|
|
|
|
|
|
|
|
k |
|
зробити додатково n |
> |
кроків. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
lg 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основним достоїнством методу бісекцій є надійність, стійкість до помилок округлення, відсутність обмежень на вид функції f (x) (потрібно тільки
безперервність). Головний недолік – повільна збіжність до точного рішення. На практиці метод бісекцій використають у комбінації з яким-небудь
швидкозходящимся методом: методом бісекцій спочатку грубо визначають початкове наближення, а потім застосовують швидкозходящийся метод (наприклад, методНьютона).
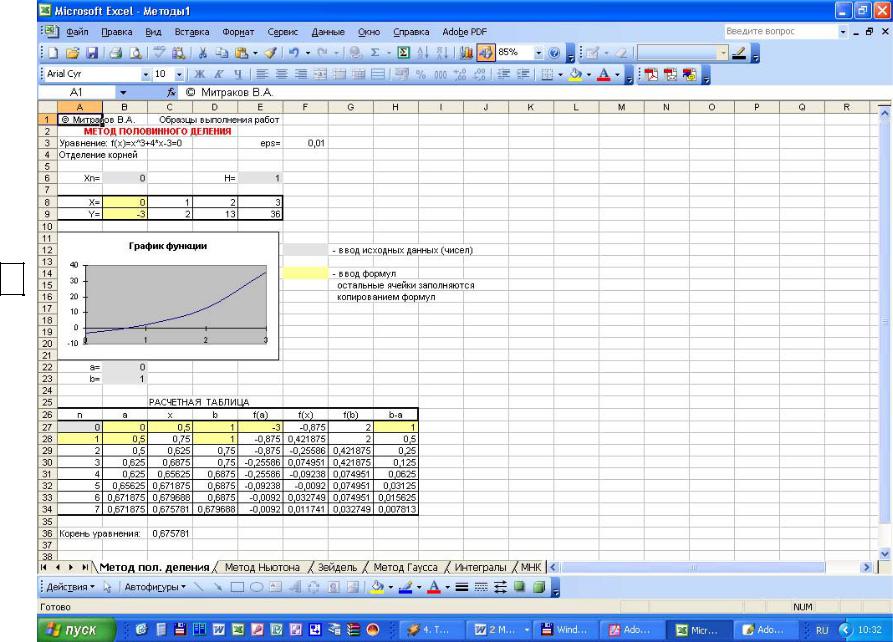
Приклад реалізації методу половинного ділення в середовищі Microsoft Excel представлена на рис. 3.3.
27
28
Рис. 3.3
Приклад
розрахунку по методу половинного ділення в
Microsoft Excel
