
- •Список прийнятих скорочень
- •Тема 1. Методи розв'язання систем лінійних рівнянь
- •Лекція 1. Метод Гауса
- •Концепція методів
- •Метод Гауса
- •Верхня трикутна система лінійних рівнянь
- •Метод виключення Гауса й вибір головного елемента
- •Схема єдиного ділення
- •Лекція 2. Ітераційні методи
- •Метод ітерацій
- •Зауваження про точність розрахунку
- •Достатня умова
- •Приведення лінійної системи до виду зручному для ітерації.
- •Метод Зейделя
- •Тема 2. Методи рішення нелінійних рівнянь
- •Лекція 3. Метод половинного ділення
- •Наближене рішення нелінійних рівнянь
- •Відділення корінь
- •Метод половинного ділення
- •Лекція 4. Метод Ньютона
- •Методика рішення задачі
- •Помилка ділення на нуль.
- •Швидкість збіжності.
- •Модифікації методу Ньютона.
- •Спрощений метод Ньютона
- •Метод Ньютона-Бройдена
- •Метод січних
- •Тема 3. Чисельне інтегрування
- •Лекція 5. Метод трапецій
- •Постановка задачі
- •Формула трапецій
- •Погрішність формули трапецій
- •Загальна формула трапецій
- •Лекція 6. Метод Сімпсона
- •Формула Сімпсона
- •Залишковий член формули Сімпсона
- •Загальна (узагальнена) формула Сімпсона
- •Тема 4. Обробка експериментальних даних
- •Лекція 7. Інтерполяція
- •Постановка задачі
- •Линейная інтерполяція
- •Квадратична інтерполяція
- •Інтерполяційна формула Лагранжа.
- •Обчислення Лагранжевых коефіцієнтів
- •Інтерполяція сплайном
- •Лекція 8. Метод найменших квадратів
- •Постановка задачі
- •Метод найменших квадратів
- •Лінійна апроксимація (інтерполяція)
- •Коефіцієнт лінійної кореляції
- •Квадратична апроксимація
- •Додатка
- •Транспонування
- •Обчислення визначника матриці
- •Знаходження зворотної матриці
- •Додавання й вирахування матриць
- •Множення матриці на число
- •Множення матриць
- •Ітераційні методи рішення рівнянь
- •Стандартні форми рівнянь
- •Пошук корінь графічним методом
- •Простий ітераційний метод здогаду й перевірки
- •Подання рівняння у формі 2
- •Пряма підстановка
- •Ітерації в осередку
- •Введення в надбудову Пошук рішення
- •Активування надбудови Пошук рішення
- •Установка надбудови Пошук рішення
- •Застосування надбудови Пошук рішення
- •Додаток 3. Контрольні питання
- •Додаток 4. Список лабораторних робіт
- •Частина 1. Обчислювальна техніка
- •Частина 2. Чисельні методи
- •Список літератури.
- •Основна література
- •Додаткова література
- •Інтернет-ресурси
|
|
|
Лекція 4. Метод Ньютона |
|
|||
Якщо |
f (x), f ' (x) і f '' (x) безперервні в околиці кореня, цю додаткову |
||||||
інформацію про властивості функції |
f (x) можна використати для побудови |
||||||
алгоритмів, які породжують послідовності, що сходяться до кореня швидше, |
|||||||
ніж при методі ділення навпіл або методі фальшивого становища. Метод |
|||||||
Ньютона-Рафсона (або просто Ньютона, також має назви метод дотичних і |
|||||||
метод лінеаризації) є одним з найбільш корисних і найвідоміших алгоритмів, у |
|||||||
якому використається безперервність |
f ' (x) |
і f '' (x). Він швидко сходиться |
|||||
(має квадратичну збіжність) і допускає різні модифікації, пристосовані для |
|||||||
рішення векторних задач і інших рівнянь. Однак, цей метод ефективний при |
|||||||
досить твердих обмеженнях на характер функції |
f (x): |
|
|||||
1. існування другій похідній функції f (x) на множині G ={a ≤ x ≤ b}; |
|||||||
2. задоволення першої похідної умові |
f ' (x)≠ 0 для всіх x G ; |
||||||
3. знакопостійність |
f ' (x), f '' (x) для всіх x G . |
|
|||||
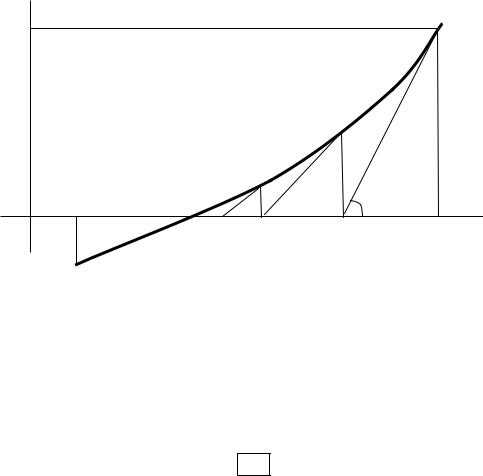
Геометрична інтерпретація методу Ньютона полягає в наступному. |
|||||||
Задається |
початкове наближення x(0) . Далі |
проводиться |
дотична до кривої |
||||
y = f (x) |
в крапці |
x(0) (рис. 4.1), тобто крива заміняється прямою лінією. Як |
|||||
наступне наближення вибирається крапка перетинання цій дотичній з віссю |
|||||||
абсцис. Процес побудови дотичних і знаходження крапок перетинання з віссю |
|||||||
абсцис повторюється доти, поки приріст не стане менше заданої величини ε . |
|||||||
f (x(0) ) |
|
|
|
|
|
В |
|
|
|
|
|
|
|
||
|
|
a |
C |
|
A |
α |
b |
|
|
|
|
||||
0 |
|
|
x* |
x(2) |
|
x(1) |
x(0) |
Рис. 4.1 |
Геометричні побудови для методу Ньютона |
||||||
Одержимо розрахункову формулу методу Ньютона. Замість ділянки кривій ВР (крапка З відповідає x* ) візьмемо ділянку АВ – дотичну, проведену в крапці
(x(0) , f (x(0) )). Для цього відрізка справедливо кінцеве співвідношення:
29

|
f (x(0) )− 0 |
|
= f ' (x |
(0) |
)≡ tgα |
(4.1) |
|||||||||||||
|
x |
(0) |
− x |
(1) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де α - кут нахилу дотичній у крапці (x(0) , f (x(0) )) до осі абсцис. |
|
||||||||||||||||||
Дозволяючи це співвідношення відносно |
x(1), одержуємо: |
|
|||||||||||||||||
|
x |
(1) |
= x |
(0) |
− |
|
f (x(0) ) |
|
|
|
|
(4.2) |
|||||||
|
|
|
|
|
|
|
f ' (x(0) ) |
|
|
|
|
|
|||||||
Повторюючи процес, знаходимо загальну формулу: |
|
||||||||||||||||||
x |
(k |
+1) |
= x |
(k ) |
− |
f (x(k ) |
) |
|
, де k = 0,1,2,... |
(4.3) |
|||||||||
|
|
|
|
|
f ' (x(k ) ) |
|
|||||||||||||
Відзначимо, що якщо відкинути ітераційний індекс, те (4.3) записується у вигляді нелінійного рівняння:
x = x − |
f (x) |
≡ϕ(x) |
(4.4) |
|
f ' (x) |
||||
|
|
|
яке, однак, на [a,b] не рівносильно вихідному, а є таким тільки в одній крапці при x = x* . Тому даний метод не служить різновидом методу простих ітерацій.
Застосуємо тепер для висновку формули (4.3) метод лінеаризації. Покладемо, що ітераційний процес має вигляд:
x(k+1) = x(k ) +δ (k ) , де k = 0,1,2,... |
(4.5) |
де δ (k ) - виправлення до k -му наближення, яку необхідно знайти.
Припускаючи, |
що |
f (x) має |
безперервну |
другу |
похідну, |
розкладемо |
f (x(k ) +δ (k ) ) |
по формулі Тейлора щодо крапки x(k ) : |
|
|
|||
f (x(k ) +δ |
(k ) )= f (x(k ) )+δ (k ) f ' (x(k ) )+ |
(δ (k ) )2 |
f "(ξ ) |
(4.6) |
||
де ξ (x(k ) , x(k+1) ) |
|
|
2 |
|
|
|
. З огляду |
на, що f (x(k ) +δ (k ) )= 0 (це |
відповідає |
||||
знаходженню крапки перетинання з віссю абсцис), і залишаючи тільки лінійну (відносно δ (k ) ) частина розкладання (звідси й назва – метод лінеаризації), записуємо лінійне відносно δ (k ) рівняння:
f (x(k ) )+δ (k ) f ' (x(k ) )= 0 |
(4.7) |
|
|
||||
Звідси виражається виправлення δ |
(k ) |
= − |
f (x(k ) ) |
Підставляючи δ |
(k ) |
|
|
|
|
. |
|
в |
|||
|
f ' (x(k ) ) |
|
|||||
(4.5), одержуємо (4.3).
Зауваження:
30

1)Із графіка видно, що якщо почати будувати дотичні із крапки а, те x(1) найдеться взагалі поза відрізком [a,b], де функція може бути навіть не
визначена. Із простих міркувань можна вивести правило вибору початкової крапки x(0) : як вихідна крапка x(0) вибирається той кінець інтервалу [a,b], якому відповідає ордината того ж знака, що й f "(x).
Ичи у вигляді формули:
|
(0) |
|
|
|
x |
a, если f (a) f "(a)> 0 |
(4.8) |
||
|
= |
f (a) f "(a)< 0 |
||
|
|
b, если |
|
|
|
|
|
|
f ' (x) і f "(x): |
2) Із графічної аналогії методу ясна вимога збереження знаків |
||||
функція на відрізку [a,b] не повинна мати перегинів і зміни монотонності.
Теорема (про достатні умови збіжності методу Ньютона):
|
Нехай виконуються наступні умови: |
|
|
|
|
|
|
|
|
|
|||||||||||||
1. |
Функція |
f (x) визначена й двічі дифференцируема на ділянці [a,b]. |
|
||||||||||||||||||||
2. |
Відрізку |
[a,b] |
належить |
тільки один |
простий |
корінь |
x* , |
так що |
|||||||||||||||
|
f (a) f (b)< 0 . |
f "(x) на [a,b] |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3. |
Похідні |
f ' (x), |
зберігають знак, і |
f ' (x)≠ 0 . |
|
|
|||||||||||||||||
4. |
Початкове наближення |
x(0) |
задовольняє |
нерівності |
f (x(0) ) f "(x(0) )> 0 |
||||||||||||||||||
|
(знаки функцій f (x) і |
f "(x) в крапці x(0) |
збігаються). |
|
|
||||||||||||||||||
|
Тоді за допомогою методу Ньютона (4.3) можна обчислити корінь |
||||||||||||||||||||||
рівняння |
|
|
f (x)= 0 з будь-якою точністю ε . |
|
|
|
|
|
|
||||||||||||||
Методика рішення задачі |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1. Задати |
) |
початкове |
|
наближення |
|
x(0) |
так, щоб |
|
виконувалася нерівність |
||||||||||||||
|
f (x(0) |
f "(x(0) |
)> 0 , а також рисе позитивне число ε . Покласти k = 0 . |
||||||||||||||||||||
2. Обчислити x |
(k+1) |
по формулі x |
(k |
+1) |
= x |
(k ) |
− |
|
f (x(k ) ) |
|
. |
|
|
|
|||||||||
|
|
|
|
f ' (x(k ) ) |
|
|
|
||||||||||||||||
3. Якщо |
|
|
x(k+1) − x(k ) |
|
≤ ε , |
процес |
завершити |
й покласти x |
x(k+1) , |
інакше |
|||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
покласти k = k + 1 й перейти до пункту 2. |
|
|
|
|
|
|
||||||||||||||||
31
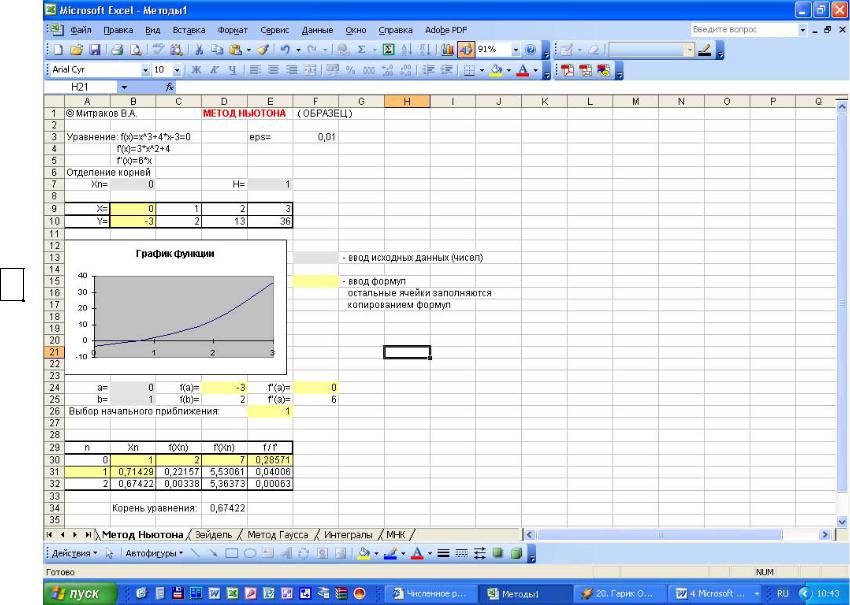
Приклад 1 рішення представлений на рис. 4.2.
32
Рис.4.2
Приклад розрахунку по методу Ньютона.
