Додаток 2.

Реалізація в MS Excel ітераційних методів

Ітераційні методи рішення рівнянь

Описуючи метод ітерацій, звичайно про нього говорять як про метод «здогаду й перевірки». Майже у всіх ітераційних методах потрібно, щоб користувач задав початкове наближення. Потім, за допомогою цього початкового наближення, вирішується рівняння й обчислюється результат, після чого виконується перевірка, у процесі якої з'ясовується, чи досить близько знайдене рішення до щирого. Якщо точність рішення, отриманого на черговому кроці, незадовільна, процес повторюється, тобто виконується нова ітерація. Для ефективного одержання ітераційних рішень важливо скласти алгоритм, по якому обробляється початкове наближення. Розглянемо наступні ітераційні методи рішення нелінійних рівнянь:

1.Пошук корінь із використанням графіка.

2.Метод здогаду й перевірки.

3.Метод прямої підстановки.

4.Метод ітерації в осередку.

5.Рішення рівнянь за допомогою надбудови Пошук рішення.

Стандартні форми рівнянь

Перед рішенням рівняння ітераційними методами його потрібно привести до стандартної форми. Розглянемо, приміром, стандартні форми рівняння x3 + 4 = 12 x (табл. П2.1).

Таблиця П2.1

Стандартні форми рівняння

У методі прямої підстановки й методі ітерації в осередку використається форма 2. Форма 1 звичайно більше зручна для пошуку рішення графічним методом; при використанні надбудови Пошук рішення застосовується різновид цієї форми (у правій частині рівняння може перебувати будь-яка константа, а не тільки нуль). Якщо пошук рішення методом «здогаду й перевірки» здійснюється вручну, то підійде кожна із цих двох форм.

Пошук корінь графічним методом

Якщо є вказівки на те, що корінь або корінь рівняння перебувають у якому-небудь кінцевому інтервалі значень, то в цьому інтервалі можна задати

68

послідовність значень. По черзі підставляючи члени цієї послідовності в рівняння, перевіряємо, наскільки добре воно задовольняється при кожному з них, причому, для наочності, дані зручно представити в графічному виді. При використанні графічного методу для пошуку корінь зручна перша форма рівняння, у якій всі його члени перенесені в одну частину. Наведене вище рівняння у формі 1 можна записати так:

рівнянню, звичайно в результаті підстановки різних значень у ліву частину рівняння точний нуль отриманий не буде (якщо тільки випадково не потрапимо на корінь). Тому перепишемо рівняння П2.1 у такому виді:

У ході пошуку рішення підставляємо різні значення змінної x , і обчислюємо значення функції f (x) й будуємо графік залежності функції

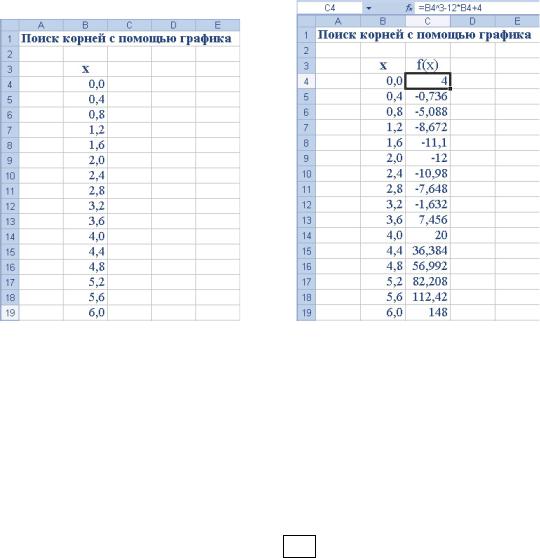
f (x) від x . Коріннями рівняння будуть значення змінної x , при яких f (x)= 0 . Спочатку введемо в електронну таблицю стовпець значень x в інтервалі 0 ≤ x ≤ 6 (рис. П2.1).

Потім для кожного x обчислимо значення f (x) (рис. П2.2).

Після цього будуємо крапкову діаграму із графіком функції f (x)

(рис. П2.3).

69

Рис. П2.4 Графік функції f (x)= x3 − 12 x + 4

70

Здіаграми П2.4 видно, щотретійкоріньперебуваєбілякрапки x = −3,8 . Графічний метод знаходження корінь досить простий, але має низьку

точність. Для знаходження корінь із більше високою точністю можуть виявитися корисними чисельні ітераційні методи. Застосовуючи ці методи, варто вказувати початкові наближення, засобом одержання яких є графічний метод.

Простий ітераційний метод здогаду й перевірки

Якщо відомо, що біля крапки x = 0,3 перебуває корінь, одним з найпростіших способів пошуку цього кореня є створення електронної таблиці, у яку вводилися б наближені значення й формула для обчислення функції f (x) (рис. П2.5).

Рис. П2.5 Обчислення функції f (x)

Потім варто підібрати таке значення x , для якого f (x) перебуває

якнайближче до нуля (у тому випадку, якщо рівняння записане у формі 1) (рис.

П2.6).

Рис. П2.6 Обчислення функції f (x)

Рис. П2.7 показує, що до кореня вдалося дібратися досить близько, однак його точне значення усе ще не знайдене, тому значення функції f (x) трохи

відрізняється від нуля. Якщо зажадати, щоб значення функції f (x) точно

рівнялося нулю, ітераційні методи можуть продовжувати свою роботу нескінченно. Замість цього пошук корінь здійснюється з точністю, що задовольняє ті або інші потреби. Для оцінки точності використається значення допуску (задана точність), що розглядається далі, а поки відзначимо, що знайдене наближення задовольняє рівнянню з точністю до двох десяткових цифр.

Іноді легше стежити за ітераційним процесом, якщо в таблиці відображені значення попередніх оцінок і відповідні їм значення функції (рис. П2.7).

71