Глава 2. Случайные величины

2.1 Дискретные случайные величины и их числовые характеристики

Большинство экспериментов завершаются появлением некоторого числа:

– в результате выявления бракованных изделий появляется число X – количественная характеристика брака;

– в результате приобретения n лотерейных билетов выявляется число X выигрышей;

– в опыте по подбрасыванию n раз монеты выявляется число X выпадения «решки»;

– при стрельбе по мишени из n опытов X оказались точными попаданиями, и т.д.

Во всех этих примерах говорится о величине, характеризующей некоторое случайное событие (опыт, эксперимент). Эти величины принимают то, или иное числовое значение в зависимости от исхода конкретного испытания.

2.1.1 Функция распределения случайной величины

Результат эксперимента  будем называть случайной величиной (СВ), если для любого xR неравенство <x является событием, т.е. определена вероятность Р(<x). Эта вероятность как функция от x называется функцией распределения (ФР) случайной величины  и обозначается F_ (x) или F(x).

Итак, по определению функцией распределения называют вероятность того, что случайная величина  в результате испытания примет значение, меньшее x:

(2.1)

Свойства функции распределения:

1. Функция распределения монотонно не убывает на R, т.е.  х₁, х₂R если х₁<х₂, то F(х₁)F(х₂).

Это очевидно, т.к. событие (<х₂) является суммой двух несовместных событий (<х₁) и (х₁<<х₂). Значит P(<х₂)=P(<х₁)+P(х₁  <х₂)P(<х₁) в силу неотрицательности вероятности.

2. Т.к. событие <+ – достоверное, а < – невозможное, то

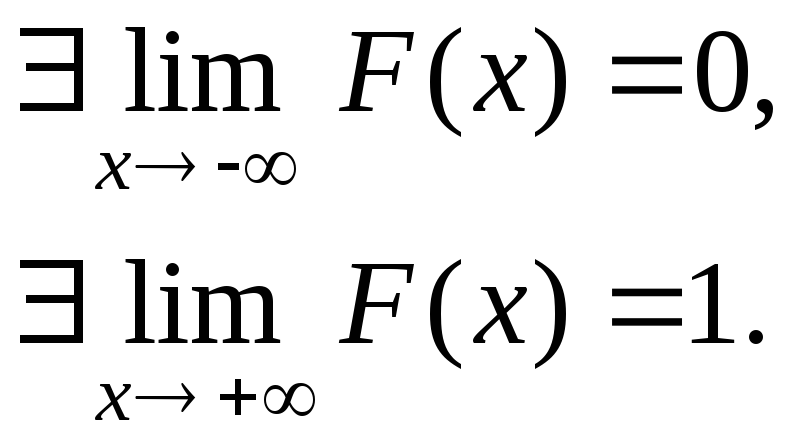
3. Поскольку функция распределения монотонна и ограничена на R, она может иметь не более чем счетное множество точек разрыва первого рода.

4. Функция распределения непрерывна слева при любом значении x:.

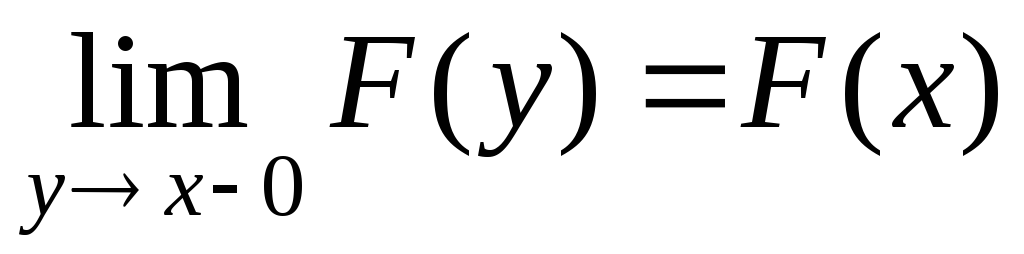5. Вероятность того, что случайная величина  примет значение в полуинтервале [a,b), равна

P{a   b}=F(b)F(a). (2.2)

6. Вероятность того, что случайная величина  примет значение в точности равное x, равна нулю: Р{=x}=F(x+0)F(x)=0.

Эти свойства непосредственно вытекают из определения функции распределения.

2.1.2 Дискретные случайные величины

Случайная величина называется дискретной (ДСВ), если она принимает отдельные, изолированные возможные значения с определенными (ненулевыми) вероятностями. Тогда каждому элементарному исходу X ставится в соответствие одно из не более, чем счетного набора пар чисел (Х₁, р₁), ..., (Х_n, p_n), n,

Правило, устанавливающее связь между значением случайной величины и ее вероятностью, называется законом распределения случайной величины.

Случайные величины обозначаются заглавными буквами латинского алфавита X,Y..., а значения, которые они принимают – прописными: x, y...

Например, дискретная случайная величина X представляет собой конечный (или бесконечный) ряд чисел x₁, x₂, x₃, ..., x_n... Его называют также рядом распределений.

Обычно закон распределения случайной величины задается в виде таблицы:

xi	x1	x2	x3	...	xn
pi	p1	p2	p3	...	pn

При этом сумма вероятностей всех возможных значений случайной величины X равна 1:

.

Задача 1. В результате подбрасывания двух игральных костей появляется некоторое число X – случайная величина, характеризующая сумму выпавших очков с определенной вероятностью. Найти закон распределения такой случайной величины X.

Решение: В этой задаче число равновозможных исходов n=66=36, а число благоприятных исходов, например, для x=4 может быть получено тремя способами (вариантами):

4=1+3=2+2=3+1.

Закон распределения такой случайной величины будет задан таблицей:

Xi	2	3	4	5	6	7	8	9	10	11	12
pi

Дискретная величина считается заданной, если указан закон ее распределения, т.е. известны все ее значения и указана вероятность каждого из них.

Так как каждому значению x ДСВ ставится в соответствие ее вероятность, то закон распределения ДСВ можно задавать с помощью функции распределения (ФР) ДСВ.

Функцией распределения F(x) ДСВ  называется вероятность события <x: F(x)=P{<x}. Очевидно, она обладает всеми общими свойствами функции распределения.

Свойства функции распределения ДСВ:

Пусть задана ДСВ X: (х_i,p­_i), p­_i0, p_i =1. Тогда

1. функция распределения непрерывна при xх_i и имеет разрыв первого рода при x=х_i, равный р_i;

2. функция распределения постоянна на полуинтервале (x_i, x_i+1­­];

3. F(x_i+0)-F(x_i)=p_i;

4. свойство накопительной вероятности:

. (2.3)

График функции распределения произвольной ДСВ представляет собой «возрастающую ступеньку». Приведем характерный вид (Рис.7) графика функции распределения ДСВ, заданной аналитически формулой

:

Пусть - некоторая детерминированная функция, определенная на пространстве элементарных исходов Ω случайной величины X. Тогда каждому возможному значению x_i случайной величины X соответствует

Рис.7

определенное значение y_i= (x_i). В таком случае исходу y_i благоприятствует элементарный исход x_i с той же вероятностью p_i, т.е. функция  задает новое пространство элементарных исходов  (Ω), на котором задана случайная величина Y, называемая функцией одного случайного аргумента Y= (X).

Если одному значению y_i соответствуют различные значения x₁… x_k, то полная вероятность осуществления y_i равна сумме вероятностей всех исходов, влекущих y_i, т.е. P(X= x₁ или… или X=x_k)==.

Пример. Дискретная случайная величина X задана рядом распределений:

X	-2	2	5
P(хi)	0.35	0.42	0.23

Составить закон распределения ДСВ Y=X².

Решение. Составим закон распределения ДСВ Y=X²:

X	-2	2	5
Х2	4	4	25
P(хi)	0.35	0.42	0.23

Т.к. двум различным значениям СВ X (x=-2, x=2) соответствуют равные значения СВ Y (y=4), то составим новый закон распределения ДСВ Y=X²_, сложив вероятности, соответствующие этим значениям СВ X:

Х2	4	25
P(хi)	0.77	0.23