2.13.3 Пуассоновский процесс
Из всех процессов, протекающих в системе с дискретными состояниями и непрерывным временем, рассмотрим те, у которых переходы системы из одного состояния в другое происходят под действием некоторых потоков событий: потока заявок, потока вызовов, потока неисправностей, потока посетителей и т.д.
Простейший
дискретный поток можно описать формулой
Пуассона для редких явлений
,
где
– среднее число заявок в единицу времени.
При переходе к непрерывному времени t
для сохранения определения величины
как числа заявок в единицу времени, ее
нужно заменить на t.
Итак, пуассоновским процессом называют случайный марковский процесс с непрерывным временем и дискретными состояниями с вероятностью:
. (2.74)
Простейший поток обладает тремя основными свойствами: ординарностью, стационарностью и отсутствием последействия. Пуассоновский поток является стационарным, т.к. его интенсивность – постоянная величина, равная среднему числу событий, наступающих за единицу времени, т.е. =MX(t)|t=1.
Поток называют ординарным, если в отдельный малый промежуток времени наступает не более одной события.
Требование отсутствия последействия означает, что события, образующие поток, появляются в последующие моменты времени независимо от того, когда и в какой последовательности.
Можно доказать, что требования ординарности, стационарности и отсутствия последействия являются достаточными для того, чтобы процесс являлся пуассоновским.
Пуассоновский поток событий обладает важным свойством: промежуток времени между двумя соседними событиями T распределен по показательному закону
P(T<t)=
,
а
его среднее значение
и среднеквадратическое отклонение(T)
равны величине, обратной ,
т.е.
где
– интенсивность потока.
Пуассоновский процесс можно описать с помощью дифференциальных уравнений Колмогорова для функций pj(t):
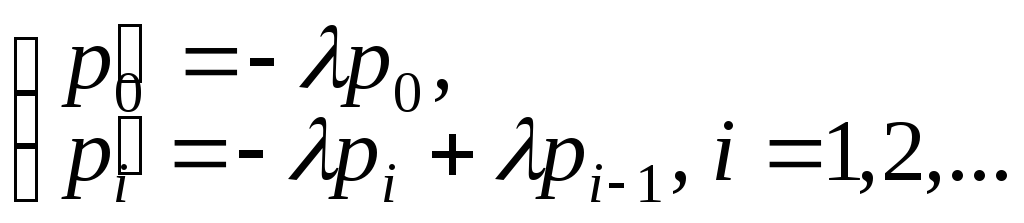(2.75)
с начальными условиями p0(0)=1, pi(0)=0, для iN. Такая система дифференциальных уравнений с указанными начальными условиями имеет единственное решение (2.80).
Отсюда видно, что ординарность пуассоновского потока приводит к тому, что элементы матрицы плотности вероятности переходов ij отличны от нуля только для j=i+1 и j=i. Простое вычисление приводит к следующей матрице
(2.76)
т.е. из состояния i можно непосредственно перейти лишь в следующее состояние j=i+1 (i=0; 1; 2;…).
Размеченный граф состояний пуассоновского процесса имеет вид (Рис.28):
Рис.28
С практической точки зрения значительный интерес представляют управляемые случайные процессы, которые возникают, например, при экономическом планировании. Так, анализируя реальную экономическую ситуацию, можно выделить как детерминированные, так и случайные факторы. К случайным факторам мы отнесем различные экономические и демографические ситуации, новейшие научные открытия, колебания спроса, метеоусловия и т.д. Для учета таких факторов используют стохастические модели. Например, зная состояние системы на начальном этапе, а также задачи, сформулированные в виде некоторого плана, можно вычислить распределение вероятностей находиться системе в каждом из возможных состояний, в том числе, в конце периода, а значит, управлять случайным процессом. В таком случае появляется возможность рассматривать совокупность решений, принимаемых на отдельном шаге, и разрабатывать стратегию поведения для принятия оптимального управленческого решения. В частности, цепи Маркова используют в реальной жизни при моделировании и прогнозировании социально-экономических процессов.