2.11 Распределения, связанные с нормальными

Нормальное распределение является исключительным в теории вероятностей, поскольку при достаточно общих условиях многие распределения стремятся по вероятности к нормальному (см. п. 2.5). В математической статистике на практике чаще всего используются три «специальных» закона распределения, получаемые из нормального – распределения Стъюдента, Пирсона и Фишера.

2.11.1 Распределение 2 (распределение к. Пирсона)

Пусть независимые случайные величины X₁, X₂, …, X_k являются стандартно нормально распределенными величинами, т.е.

X_iN(0, 1), где i=1, 2, …k.

Распределение случайной величины

называется распределением «хи-квадрат» с k степенями свободы, а сама величина ²(k)0 – величиной «хи-квадрат с k степенями свободы». Если величины X₁, X₂, …, X_k не являются независимыми (т.е. между ними существует l1 функционально независимых уравнений связи), то число независимых случайных величин будет равно разности между числом суммируемых случайных величин и числом связей, ограничивавших свободу изменения этих величин, т.е. kl. Если все уравнения связи линейны, то тогда величина будет также распределена по² , но с kl степенями свободы. Число степеней свободы является единственной числовой характеристикой таких случайных величин, следовательно, все числовые характеристики случайной величин ²(k) (функция распределения, математическое ожидание, дисперсия и т.д.) должны зависеть от единственного параметра k.

Функция распределения случайной величины

имеет довольно сложный вид:

. (2.57)

Функция распределения позволяет написать плотность вероятности, которая оказывается элементарной функцией:

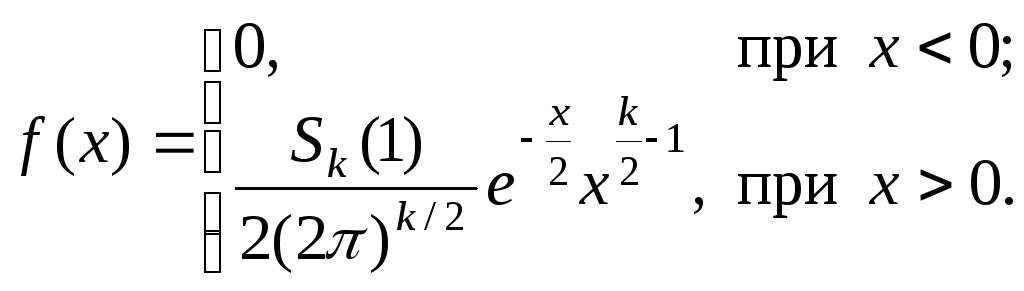(2.58)

Графики плотности вероятности для разных значений k представлены на рис. 24.

Рис.24

Из рис. 24 и уравнения (2.61) видно, что распределения с k=1 и k=2 являются особенными, т.к. не обращаются в ноль при x=0. При k=1 распределение не имеет моды вообще, при k=2 мода расположена в нуле: Mo(²(2))=0.

Свойства распределения :

1) ²(k)0;

2) M(²(k))=k;

3) D(²(k))=2k;

4) Mo(²(k))=k2;

5) асимметрия A(²(k))=;

6) эксцесс Е(²(k))=;

7) если СВ ²(k₁) и ²(k₂) независимые, то их сумма имеет «хи-квадрат» распределение с числом степеней свободы k₁+ k₂, т.е.

²(k₁) +²(k₂)=²( k₁+k₂).

Т.о., ²(k) – распределение, зависящее лишь от числа степеней свободы k, причем с увеличением k это распределение, согласно центральной предельной теореме (п. 2.12), медленно стремится к нормальному. Так, при k>30 распределение случайной величины Z= приближается к стандартному нормальному распределению N(0,1).

2.11.2 Распределение Стъюдента

Пусть Z и V независимые случайные величины, причем ZN(0,1), а V[²(k)].

Тогда распределение случайной величины называютt–распределением Стъюдента с k степенями свободы. С возрастанием числа степеней свободы это распределений быстро приближается к нормальному. График плотности вероятности распределения Стъюдента похож на нормальный и имеет вид (рис.25):

Рис.25

Свойства распределения Стьюдента:

1) М(T_k)=Мо(T_k)=Ме(T_k)=0;

2) D(T_k )= и существует только при k>2;

3) A(T_k)=0;

4) Е(T_k)=и существует только приk>4.

Значения ²-распределения и t-распределения (Стъюдента), зависящие лишь от степени свободы, затабулированы.