Глава 1. Основные понятия и теоремы теории вероятностей

Под событием принято понимать всякий факт, который может произойти в данных условиях. Совокупность условий, при которых событие может произойти, а может не произойти, назовем заданным комплексом условий S. Под испытанием, опытом или экспериментом понимают реализацию (воспроизведение) этого комплекса условий S. Случайным называется такое событие, которое может произойти, а может не произойти при заданном комплексе условий S. Каждое событие является совокупностью элементарных событий. Элементарным событием (исходом) назовем каждый из возможных результатов случайного испытания.

Множество всех возможных в результате испытаний элементарных событий называется пространством элементарных событий и обозначается .

В зависимости от результата исходов многократного воспроизведения заданного комплекса условий S, события можно классифицировать:

	События
Детерминированные (исход однозначен)	Случайные (исход неоднозначен)	Неопределенные (нельзя проводить многократные испытания)

Заранее известен исход во многих явлениях классической физики. Поэтому классическую физику и называют детерминированной, т.к. исходы тех или иных событий и явлений определены однозначно.

В то же время нельзя определить результат исхода войны или матча, т.к. их невозможно повторить, сохранив все начальные условия без изменений.

Если при повторении некоторого начального комплекса условий будущее состояние системы определено не однозначно, а лишь с некоторой вероятностью, то рассматривают случайные события: выявление бракованной детали, результат стрельбы по мишени и т.д.

Теория вероятностей изучает свойства массовых случайных событий, способных многократно повторяться при воспроизведении определенного комплекса условий, а также при взаимодействии большого числа случайных факторов.

1.1 Виды случайных событий. Операции над событиями

Обозначать события принято заглавными буквами латинского алфавита: A, B, C и т.д. Рассмотрим отдельные виды событий и отношения между ними.

1. Достоверным называется событие “” (или U), если оно обязательно произойдет в данном испытании в результате выполнения комплекса условий S.

2. Невозможным называется событие “” (или V), если это событие никогда не произойдет в данных испытаниях в результате выполнения совокупности условий S.

Например, монета не может одновременно выпасть орлом и решкой.

3. Суммой (или объединением) событий A и B называется событие 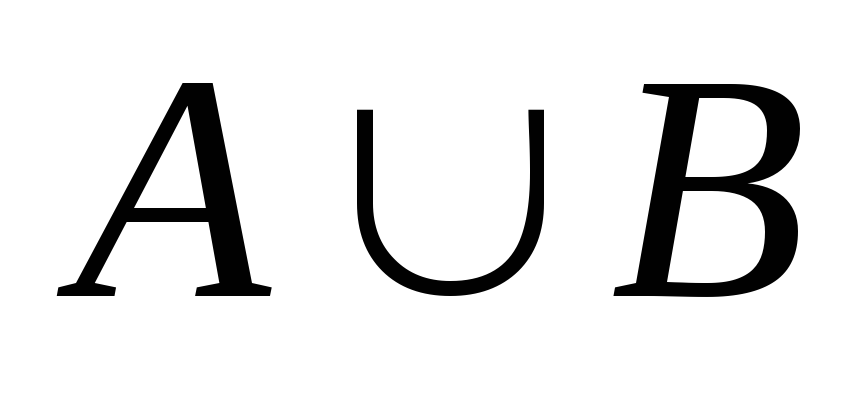(A+B), состоящее в наступлении хотя бы одного из событий A или B. Для применения правила суммы используют “ключевое” слово «или».

4. Произведением событий A и B называется событие 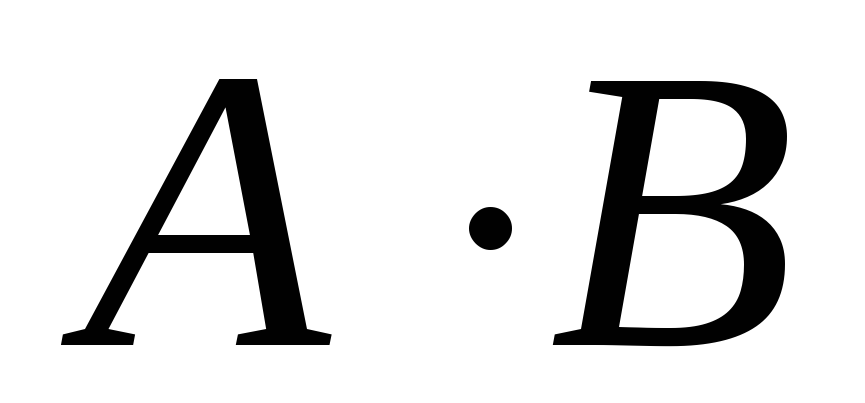, AB, состоящее в совместном выполнении одновременно и события A, и события B. Варианты записи: АВ, ВА, 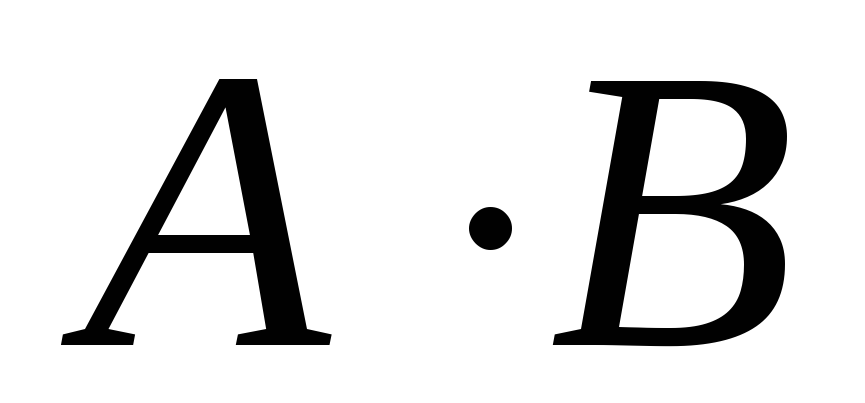. Для применения правила произведения используют “ключевое” слово «и».

5. Несовместными называют события, если наступление одного из них в том же испытании исключает наступление другого.

Например, несовместными будут события «деталь – стандартная» и «деталь является бракованной». Т.о., два события A и B несовместны, если их произведение есть невозможное событие: AB=.

6. Несколько событий образуют полную группу событий, если в результате испытаний произойдет хотя бы одно из них. В частности, совокупность несовместных событий A_i образует полную группу событий, если в результате единичных испытаний произойдет обязательно одно из этих событий:

, где nR, A_iA_j для ij.

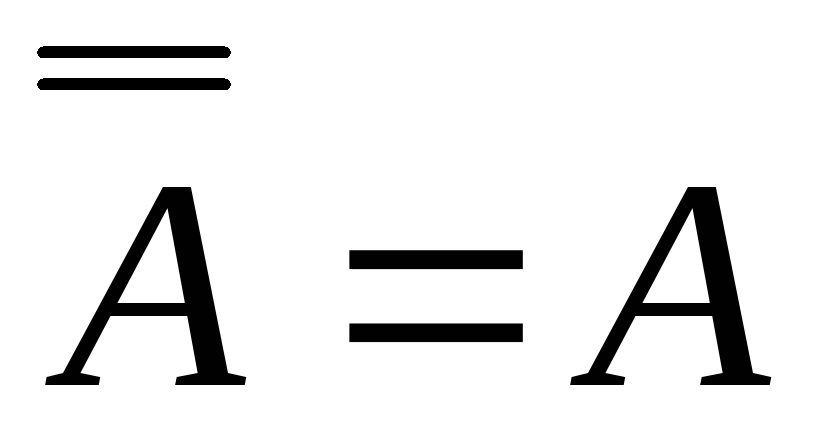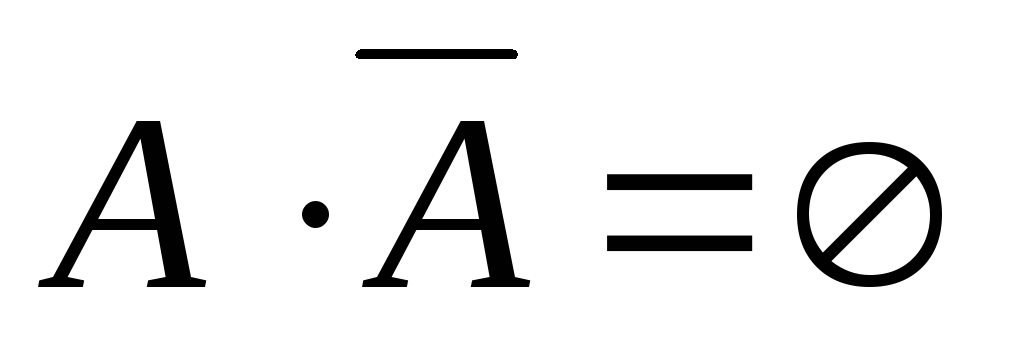7. Противоположными называются два несовместных события A и , образующие полную группу событий (– отрицаниеA, читается – “неA”). Для противоположных событий справедливо тождество (двойное отрицание снимается). Произведение противоположных событий– есть событие невозможное. Сумма противоположных событий – есть событие достоверное:.

Так, противоположными являются события «поражение мишени» и «промах» («третьего не дано»).

8. Благоприятствующими событию A называют те элементарные исходы, при которых наступает изучаемое событие A.

9. Равновозможными называют такие элементарные события, которые при создании комплекса условий S имеют одинаковые шансы для их наступления.

Так, равновозможны выпадения цифр 5 и 3 при одноразовом бросании симметричного кубика (игральной кости).

1.2 Определения вероятности

Количественной мерой степени возможности осуществления события в заданном комплексе условий S служит вероятность. Вероятность события A обозначается Р(A) или Р{A}. Дадим классическое определение вероятности.

Вероятностью события A называется отношение числа исходов m, благоприятствующих наступлению события A, к числу n всех несовместных равновозможных элементарных исходов, образующих полную группу событий:

P(A) = . (1.1)

Из определения вероятности следует, что вероятность удовлетворяет условиям

0  P(A)  1, P( )1, P()0.

Ограниченность применения классического определение вероятности связана с тем, что оно применяется только тогда, когда:

1. число элементарных исходов конечно;

2. результаты всех испытаний или наблюдений равновозможны;

3. все равновозможные события образуют полную группу попарно несовместных событий.

Если не удается подсчитать m и n для вычисления вероятности из-за нарушения перечисленных условий, то можно воспользоваться или геометрическим, или статистическим определением вероятности.

Геометрическое определение вероятности связано с вероятностью попадания точки в некоторую область, являющуюся геометрическим объектом (множество точек отрезка, части плоскости или пространства). Пусть событие A представляет собой попадание точки в область gG, а попадание в измеримую область G достоверно. Вычислим вероятность попадания произвольно взятой точки в некоторую область (событие A), которая пропорциональна мере этой части и не зависит от ее формы и расположения. Это может быть или мера длины, или площади, или объема и т.д., в зависимости от пространства элементарных событий. Обозначим это понятие меры через mes. Например, для подмножества плоскости gGR², мера (mes) есть площадь (Рис. 1).

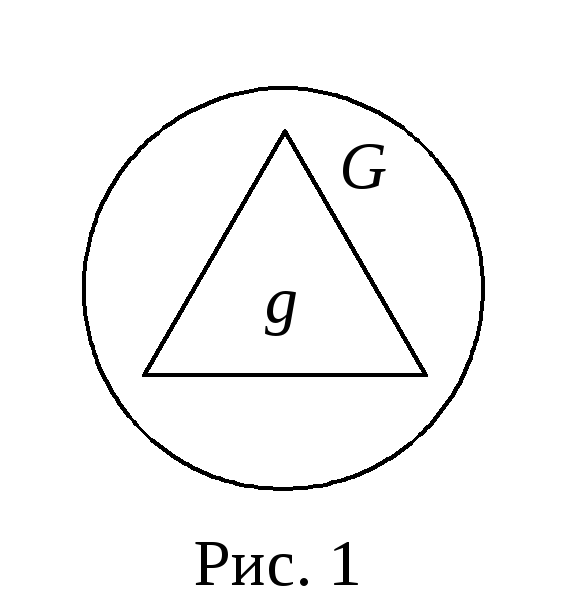
Тогда геометрической вероятностью назовем отношение меры подмножества g к мере множества G:

Р(A)= . (1.2)

Статистическое или частотное определение вероятности связано с понятием частоты событий. В отличие от классического определения вероятности, для подсчета относительной частоты необходимо выполнить серии реальных испытаний.

Относительной частотой события A называется отношение числа m испытаний, при которых событие A произошло (или m(A)), к общему числу всех фактически произведенных испытаний n, при проведении которых событие A могло произойти или не произойти.

Обозначается относительная частота или .

При достаточно большом числе испытаний, вероятность появления события A почти совпадает с частотой появления A, т.е. Р(A)W(A), что проявляется в законе больших чисел Якоба Бернулли (п. 2.12). Массовые случайные события обладают свойством статистической устойчивости частоты: т.е. значения частоты появления события A, полученные в результате многократных испытаний, колеблются около некоторого постоянного числа, которое и является вероятностью этого события. Поэтому относительную частоту и называют статистической вероятностью. Отличие статистического определения вероятности от классического заключается в том, что по классическому определению вероятность вычисляется до проведения эксперимента, а согласно статистическому определению – по результату опытного исследования.

Для построения теории вероятностей как строгой (дедуктивной) науки необходимо познакомиться с аксиоматическим определением вероятности.

Аксиоматическое определение вероятности было предложено А.Н.Колмогоровым в 30-е годы XX века. Неопределяемым понятием является произвольное множество , называемое пространством элементарных исходов. На  построим множество всех его подмножеств F, которое назовем пространством событий. На F определена алгебра событий, т.к. выполняются требования:

1. F, F.

2. Если AF и BF, то A+BF, ABF, F.

Определение вероятности сформулируем в виде аксиом:

1) Каждому случайному событию A пространства событий F ставится в соответствие неотрицательное число Р(A)0, называемое вероятностью (т.е. всюду на F определена числовая функция P: FR₊).

2) Вероятность достоверного события равна единице: Р()=1.

3) Если события А₁, А₂, ... А_i,.. – попарно несовместны, то вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий:

. (1.3)

Благодаря введению аксиоматического определения, удалось представить теорию вероятностей в виде стройной математической науки.

1.3 Некоторые теоремы теории вероятностей

Сформулируем и докажем некоторые свойства вероятности. Частным случаем аксиомы сложения является вероятность суммы несовместных событий.

1. Вероятность суммы несовместных событий (Рис.2) равна сумме вероятностей этих событий: (ключевое слово “или”):

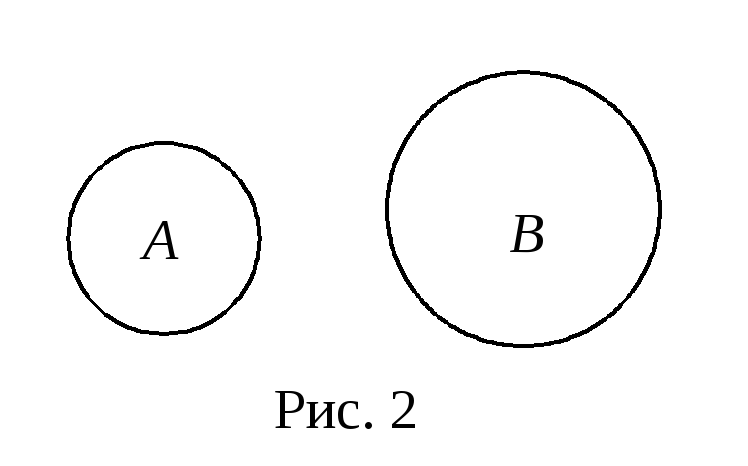
P(A+B) = Р(A)+Р(B).

2. Вероятность полной группы событий равна единице: .

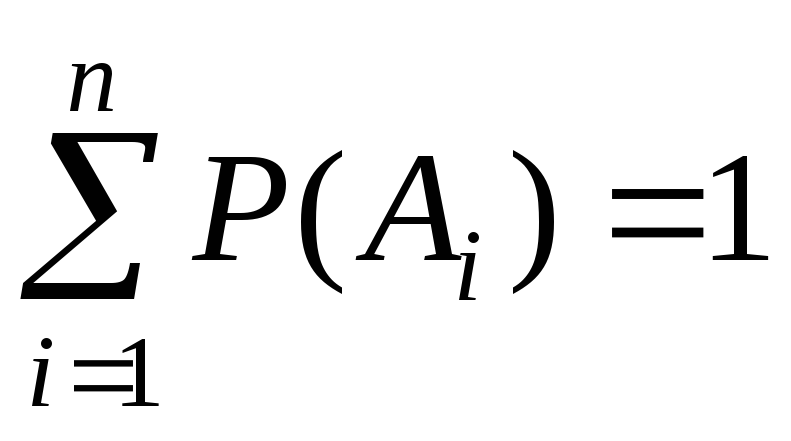3. Вероятность суммы противоположных событий равна единице:

,

так как сумма противоположных событий есть событие достоверное и P()=1. Тогда вероятность события , противоположного событию A, равна

Р()=1–Р(A). (1.4)

Очевидно, что вероятность произведения противоположных событий равна 0, т.е. Р()=0, так как это событие невозможное: .

4. Если событие A влечет за собой событие B, т.е. AB, то P(A)≤P(B).

Действительно, если AB, то P(A)+P(B|A)=P(B) как вероятность суммы несовместных событий. Тогда, согласно аксиоме 1, Р(A)0; отсюда P(A)≤P(B).

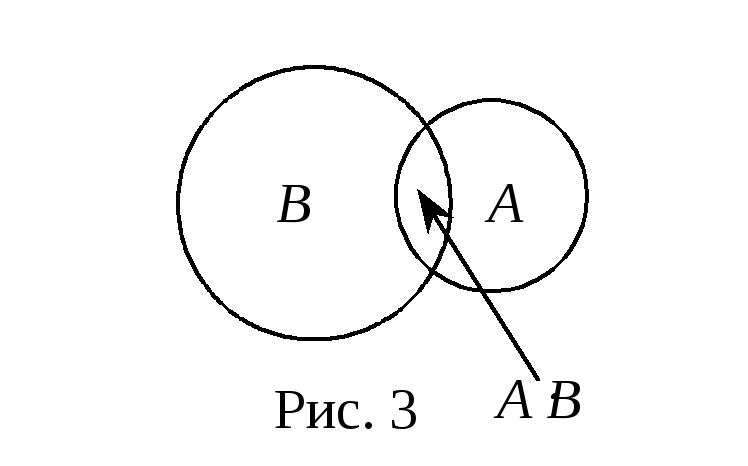
5) Вероятность суммы двух совместных событий (Рис.3) вычисляется по формуле:

P(A+B)=P(A)+P(B)–P().(1.5)

Доказательство. Известно, что так как события A и B совместные, то по определению сумма “A+B” означает или “A”, или “B”, или оба вместе, т.е. событие A+B произойдет при наступлении одного из трех несовместных событий либо , либо, либоAB. Тогда по теореме сложения вероятности несовместных событий имеем

Событие A произойдет при наступлении одного из двух несовместных событийилиAB. Тогда по теореме сложения вероятности несовместных событий имеем Отсюда выразим вероятность

Аналогично, событие B произойдет при наступлении одного из двух несовместных событийилиAB. Тогда по теореме сложения вероятности несовместных событий имеем: Отсюда выразим вероятность

Подставив полученные выражения в формулу вероятности суммы несовместных событий, имеем

P(A+B)=(P(A)–P(AB))+(P(B)–P(AB))+P(AB)=P(A)+P(B)–P(AB).

Замечания.

1. Формула вероятности суммы несовместных событий является частным случаем полученной формулы, т.к. для несовместных событий вероятность их одновременного осуществления равна нулю. Т.о., при P(AB)=0 эта формула принимает вид: P(A+B)=P(A)+P(B).

2. Для трех событий A, B и C справедлива формула:

Р(A+B+C)=Р(A)+Р(B)+Р(C) –Р()–Р()–Р()+Р().

Условная вероятность. Для событий A и B введем условную вероятность Р(A|B) (альтернативное обозначение P_B(A)) – вероятность того, что событие A произойдет при условии, что произошло событие B.

Условная вероятность того, что произойдет событие A, при условии, что событие B произошло, вычисляется по формуле

, где P(B)≠0. (1.6)

Тогда справедлива теорема: Вероятность совместного появления событий A и B равна произведению вероятности одного события на условную вероятность другого, при условии, что первое событие произошло (ключевое слово “и”) и находится по формуле

Р(АВ)=Р(A|B)=Р(B|A). (1.7)

Событие A называется независимым от события B, если появление события B не изменит вероятность появления события A, т.е. Р(A|B)=Р(A). Если A не зависит от B, то согласно формуле 1.7 событие B не зависит от A, т.е. они попарно (взаимно) независимы.

Тогда вероятность произведения независимых событий A и B равна произведению их вероятностей:

Р()=Р(A). (1.8)

Полученное равенство может служить определением независимых событий. Если два события не являются независимыми, то они называются зависимыми. Заметим, что если событие A зависит от исхода B, то Р(A|B)Р(A).

Пусть дано некоторое множество событий A={A₁,…, A_k}. Элементу A_pA поставим в соответствие множество B_p, составленное из произвольных комбинаций (произведений) из числа оставшихся событий, где каждое представлено не более одного раза. Тогда события A₁,…, A_k, называются независимыми в совокупности, если для любого pk и любого события CB_p события A_p и C попарно независимы.

Следствия.

1. Если события A₁,…, A_k независимы в совокупности, любое их подмножество независимо в совокупности.

2. Если события A₁,…, A_k независимы в совокупности, вероятность их совместного осуществления равна произведению их вероятностей, т.е.

Р()=P(A₁)(A₂). (1.9)

3. Вероятность совместного осуществления нескольких событий равна произведению вероятности одного из них на условную вероятность всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошли:

.

Задача 1. В денежно-вещевой лотерее из 1000 билетов 24 денежных и 10 вещевых выигрыша. Вы приобрели два билета. Какова вероятность, что выиграют не менее одного билета?

Решение. Пусть A - выигрыш по I билету, B - по II билету. Так как выигрышных 24+10=34 билета, то P(A)=0.034, а вероятность проигрыша по I билету P()=1P(A)=0.966. Чтобы найти вероятность выигрыша хотя бы по одному из двух билетов, мы от единицы вычитаем вероятность проигрыша сразу по двум билетам P() (и по первому, и по второму). Так как приобретены два билета, то вероятность проигрыша по второму билету, при условии, что первый проиграл, есть условная вероятность (т.к. теперь могут выиграть 34 билета из 999). Поэтому , а.

Тогда: P=1P()=1P()=1.

Задача 2. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0.95; второй - 0.9. Какова вероятность того, что при аварии сработает только один сигнализатор?

Решение. Обозначим буквой A событие ”сработает только один сигнализатор”, B – ”сработает первый”, C – ”сработает второй сигнализатор”. Тогда,

P(B)=0.95; P()=1P(B)=10.95=0.05,

P(C)=0.9; P()=1P(C)=10.9=0.1

Получить желаемый результат можно двумя способами: или сработает первый, а второй при этом не работает, или сработает только второй, и при этом первый не сработает. Операции между событиями при этом имеют вид: . Тогда вероятность того, что сработает только один сигнализатор:

Р(A)=Р(B)Р()+Р()Р(C)=0.950.1+0.90.05=0.14.

Задача 3. Вероятность правильного оформления счета составляет 0.8. Во время аудиторской проверки были взяты для анализа два счета. Какова вероятность, что хотя бы один счет оформлен правильно?

Решение: а) Пусть событие A – правильно оформлен как минимум один счет, события B₁ и B₂ – правильно оформлены соответственно первый и второй счет. Известно, что P(B₁)=P(B₂)=0.8; тогда . Так как могут быть правильно оформленыили первый, или второй, или оба счета вместе (), то вероятность правильно оформить хотя бы один счет складывается из суммы трех несовместных событий:

.

Итак, P(A)=0.96.

б) Второй способ решения задачи связан с полной группой событий, т.к. кроме перечисленных вариантов существует четвертый – оба счета с ошибками. Вероятность допустить ошибки в оформлении двух счетов равна вероятности произведения этих независимых событий . Тогда вероятность противоположного события – правильно оформить оба счета – равна P(A)=10.04=0.96.

в) Эту задачу можно было решить и третьим способом – по правилу суммы совместных событий. Очевидно, A=B₁+B₂ Согласно формуле 3.5, имеем:

P(A)=P(B₁)+P(B₂)-P(B₁)P(B₂)=0.8+0.8-0.80.8=0.96.

Очевидное преобразование при переходе от второго способа к третьему – закон двойственности де Моргана,

,

справедливый для любых множеств.

Задача 4. Прибор, работающий в течение суток, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность любого из узлов выводит из строя весь прибор. Вероятность исправной работы в течение суток первого узла равна 0.9, второго – 0.85, третьего – 0.95.

а) С какой вероятностью прибор будет работать в течение суток безотказно?

б) Какова вероятность выхода из строя в течение суток хотя бы одного узла?

в) Какова вероятность выхода из строя в течение суток одного узла?

г) Какова вероятность, что в течение суток не менее одного узла будут работать безотказно?

д) Какова вероятность, что в течение суток не менее двух узлов выйдут из строя?

Решение: Обозначим через A, B и C события, состоящие из того, что соответственно узлы I, II, и III исправно проработают в течение суток, через D - вероятность того, что прибор безотказно работает в течение суток.

Известно, что P(A)=0.9, P(B)=0.85, P(C)=0.95.

а) Так как события A, B и C независимые, то вероятность того, что и первый, и второй, и третий узел в течение суток будут работать безотказно, находится с помощью теоремы о произведении независимых событий (1.9):

P(D )=Р()=Р(A)=0.90.850.95=0.726750.727.

б) События - «выход из строя в течение суток хотя бы одного узла» иD - «безотказная работа в течение суток» - противоположные.

Тогда Р=1 0.727=0.273.

в) Вероятности выхода из строя I, II, и III узла соответственно равны Р=1– 0.9=0.1;P; P. Тогда выход из строя в течение суток одного узла – событие E =, состоящее из суммы трех несовместных событий (один из узлов отказал, а остальные два работают), каждое из которых есть произведение независимых событий (работа одного из узлов).

Тогда Р(Е)=0.9 0.85 0.05+0.1 0.85 0.95+0.9 0.15 0.95=0.246.

г) Событие К - «не менее одного узла будут работать безотказно» противоположно событию - «менее одного узла будут работать безотказно», т.е. выходу из строя всех трех узлов одновременно. Поэтому находим его вероятность по формуле

Р(К)=1– Р(=1–Р РР=1– 0.1 0.15 0.05= 0.9992.

На основании полученных данных можно сделать вывод, что событие «не менее одного узла будут работать безотказно» «практически достоверное».

д) Событие М - «не менее двух узлов выйдут из строя» противоположно событию - «менее двух узлов выйдут из строя», т.е. или один окажется неисправным (Е), или менее одного узла будут неисправны, т.е. все работают безотказно (D). Поэтому надо либо непосредственно найти вероятность события М – выход из строя двух (H) или трех узлов (, либо находить вероятность противоположного события – «менее двух узлов выйдут из строя».

I вариант: Р(М)= Р(H)+Р(, где событие

H=

II вариант: Р(М)=1Р()= 1(Р(Е)+ P(D ))=1(0.246+0.727)=0.027.

Мы выбрали формулу решение задачи вторым вариантом как более рациональным.