1.7 Формула Байеса. Вероятность оценки гипотез

Пусть в ходе испытания событие A осуществилось вместе с одним из n попарно несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу событий то есть . Найти вероятность каждой отдельной гипотезыH₁, H₂, ..., H_n, при условии выполнения события A, можно по формуле Байеса.

Вероятность гипотезы H_i при условии, что событие A произошло, обозначим P(H_i|A).

По теореме произведения зависимых событий вероятность одновременного осуществления и события A, и гипотезы H_i равна:

P(AH_i)=P(H_i|A)P(A)=P(A|H_i)P(H_i).

Тогда вероятность гипотезы H_i при условии, что событие A произошло, найдем, выразив из последних двух произведений неизвестный множитель P(H_i|A) по формуле

. (1.14)

Заменяя P(A) суммой произведений по формуле полной вероятности, получим:

.

Формула Байеса дает возможность переоценивать вероятности гипотез, принятых до испытаний, по результатам вновь произведенных испытаний (уточнение гипотез).

Задача 19. Рассмотрим подробно ключевую задачу:

Имеются три урны с шарами: в первой - 4 белых и 6 красных, во второй – 7 белых и 3 красных, в третьей – 8 белых и 2 красных. Бросают игральную кость. При выпадении одного, двух, трех очков вынимают шар из первой урны, если выпали четыре очка – из второй, другое количество очков – из третьей урны.

а) Найти вероятность того, что вынутый шар – белый.

б) Вынутый шар оказался белым. Из какой урны наиболее вероятно он мог быть извлечен?

Решение. Примем в качестве гипотез событие Hi – извлечь шар из i-ой урны, где i={1,2,3}.

а) Найдем вероятности гипотез.

Вероятность выпадения одной из трех граней с одним, двумя и тремя очками P(H₁)=3/6=1/2 – вероятность первой гипотезы (H₁).

Вероятность второй гипотезы (H₂) выпадения четырех очков равна P(H₂)=1/6.

Вероятность третьей гипотезы (H₃) – выпадение других очков, т.е. пяти или шести, равна P(H₃)=2/6=1/3. Т.к. гипотезы составляют полную группу событий, то сумма их вероятностей равна единице:

P(H₁)+P(H₂)+P(H₃)=1/2+1/6+1/3=1.

Заметим, что условие выбора гипотезы могло быть записано отношением 3:2:1. Вероятность извлечения белого шара (A), при условии, что он вынут из i-ой урны, равна P(A|H_i). Тогда полная вероятность события A – извлечения белого шара из одной из трех урн равна:

P(A)=∑P(A|H_i)P(H_i)=2/51/2 + 7/101/6 + 4/51/3 = 7/12.

б) Для того, чтобы установить из какой урны наиболее вероятно извлечь белый шар, надо сравнить вероятности извлечения белого шара из каждой урны. Вычислим вероятность гипотез Hi, где i={1,2,3}, при условии, что событие A произошло по формуле 1.14, и занесем все данные в таблицу и вычислим вероятности гипотез при условии, что событиеA произошло, по формуле (1.14).

События	Вероятности
Гипотезы	P(Hi)	P(A|Hi)	P(Hi|A)
H1	P(H1)=1/2	P(A|H1)=2/5	P(H1|A)==12/35
H2	P(H2)=1/6	P(A|H2)=7/10	P(H2|A)==1/5=7/35
H3	P(H3)=1/3	P(A|H3)=4/5	P(H3|A)==16/35
P(A)	P(A)==1/22/5+1/67/10+1/34/5=35/60=7/12

Из трех вариантов наибольшая вероятность извлечь белый шар из третьей урны, т.к. вероятность P(H₃|A)=16/35 – максимальная. Поэтому можно сделать вероятностный вывод, что белый шар скорее всего извлечен из третьей урны.

Задача 20. Статистика запросов кредитов в банке такова: 10% - государственные органы, 30% - другие банки, остальные – физические лица. Вероятности невозврата взятого кредита соответственно равны: 0.01; 0.05 и 0.2. Найти вероятность невозврата очередного запроса на кредит. Начальнику кредитного отдела доложили, что получено сообщение о невозврате кредита, но в факсовом сообщении имя клиента было плохо пропечатано. Какова вероятность, что данный кредит не возвращает какой-то банк?

Решение. 1) Вероятность невозврата найдем по формуле полной вероятности. Пусть H₁ означает, что запрос поступил от государственного органа, H₂ – от банка, H₃ – от физического лица и событие A – невозврат рассматриваемого кредита. Тогда

=

=0.10.01+0.30.05+0.60.2=0.136.

2) Вероятность того, что данный кредит не возвращает какой-то банк, найдем по формуле Байеса:

.

Задача 21. Из 10 учеников, пришедших на экзамен по математике, 3 ученика подготовились отлично, 4 – хорошо, 2 – удовлетворительно, а 1 – не готовился вообще. Из 20 экзаменационных вопросов первые 3 ученика могут ответить на все 20 вопросов, хорошо подготовившиеся на 16 вопросов, удовлетворительно – на 10, не подготовившийся ученик помнит лишь 5 вопросов с лекций, на которых присутствовал.

Экзаменующийся ученик ответил на все 3 вопроса. Какова вероятность того, что он отличник?

Решение. Введем обозначения:

Пусть A - ученик ответил на N_i вопроса,

событие Н₁ – ученик подготовился на “5”,

событие Н₂ – ученик подготовился на “4”,

событие Н₃ – ученик подготовился на “3”,

событие Н₄ – ученик к экзамену не готов.

Тогда Р(Н₁)=0.3; Р(Н₂)=0.4; Р(Н₃)=0.2; Р(Н₄)=0.1

Вероятность ответить на все три вопроса для тех, кто подготовился

на “5” – Р(A|Н₁)=1,

на “4” – Р(A|Н₂)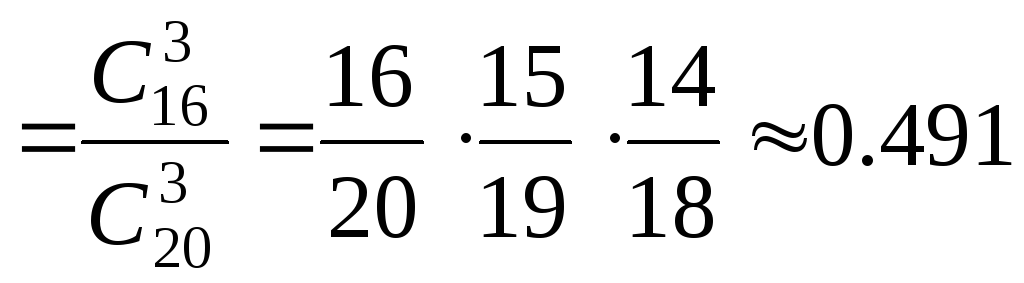(ответили на 1, и на 2, и на 3 вопрос, а после каждого ответа, количество предлагаемых вопросов на один уменьшалось).

Для троечника Р(A |Н₃)=.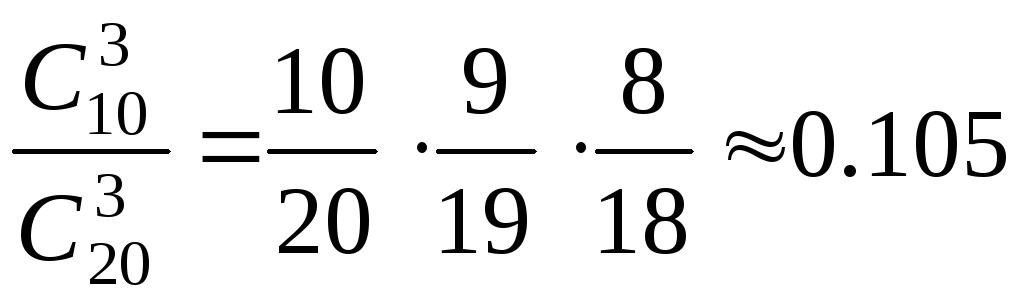

Для лентяя Р(A |Н₄).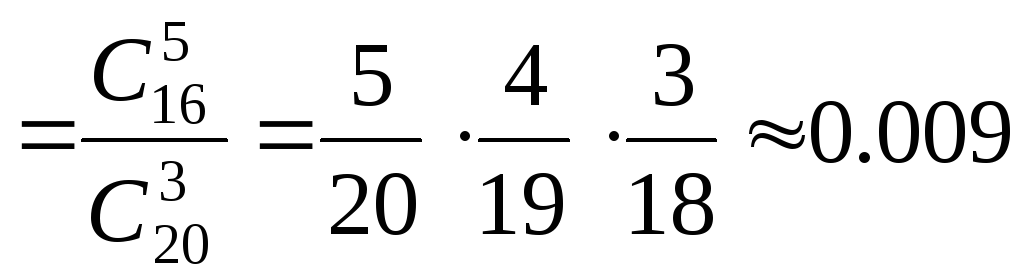

По формуле Байеса найдем вероятность, что ответивший – отличник:

Р(Н₁|A)=.

Так как вероятность невелика, учитель не сразу ставит «отлично», а задает дополнительные вопросы.

Задача 22. При обследовании больного у врача возникли подозрения на одно из двух близких по характеру заболеваний Н₁ и Н₂. Их вероятность в данной ситуации Р(Н₁)=0.6 Р(Н₂)=0.4, т.е. больной действительно болен или Н₁, или Н₂. Для уточнения диагноза больной дообследуется, сдав анализы. Если результат дообследования положительный, то вероятность первого заболевания 0.9, если отрицательный, то 0.1. В случае второго заболевания положительная и отрицательная реакции равновероятны.

В результате двукратного проведения дообследования, реакция дважды оказалась отрицательной. Необходимо найти вероятность каждого заболевания Н₁ и Н₂ после дообследования.

Решение. Обозначим через A событие, заключающееся в отрицательном результате дообследования.

Для заболевания Н₁ вероятность Р(A|Н₁)=0.10.1=0.01 (и в I, и во II случаях результат анализа отрицательный). Аналогично, для Н₂ вероятность Р(A|Н₂)=0.50.5=0.25. Найдем вероятность первого заболевания в случае, если произошло событие A, по формуле Байеса:

.

Аналогично

.

Поэтому врач остановился на гипотезе, что у больного второе заболевание.