
- •Введение
- •Глава 1. Основные понятия и теоремы теории вероятностей
- •1.4 Элементы комбинаторики
- •1) Правило суммы.
- •2) Правило произведения.
- •3) Перестановки.
- •1.5 Применение комбинаторики для подсчета вероятностей
- •1.7 Формула Байеса. Вероятность оценки гипотез
- •1.8 Независимые повторные испытания. Формула Бернулли
- •1.9 Наивероятнейшее число наступления события
- •1.10 Формула Пуассона
- •1.11 Локальная и интегральная теоремы Муавра-Лапласа
- •Глава 2. Случайные величины
- •2.1.2 Дискретные случайные величины
- •2.1.3 Числовые характеристики дискретной случайной величины
- •Свойства математического ожидания:
- •2.2 Биномиальное распределение дсв
- •Закон распределения такой дсв имеет вид:
- •2.3 Геометрическое распределение дсв
- •2.4 Закон распределения Пуассона
- •2.5 Непрерывные случайные величины и их числовые характеристики
- •2.5.1 Плотность распределения вероятностей
- •2.5.2 Числовые характеристики непрерывной случайной величины
- •2.6 Нормальное распределение и его числовые характеристики
- •2.8 Показательное распределение
- •2.9 Числовые характеристики случайной величины (продолжение). Моменты
- •2.10 Случайные векторы. Закон распределения
- •2.10.1 Случайные векторы
- •2.10.2 Зависимые и независимые случайные величины
- •2.11 Распределения, связанные с нормальными
- •2.11.1 Распределение 2 (распределение к. Пирсона)
- •Функция распределения случайной величины
- •2.11.3 Распределение Фишера-Снедекора (или f-распределение)
- •2.12 Понятие о законе больших чисел
- •2.12.1 Неравенство Маркова
- •2.12.2 Неравенство Чебышева
- •2.12.3 Теорема Чебышева
- •Но т.К. Вероятность не превышает единицы, то справедливо
- •2.12.4 Теорема Бернулли
- •2.12.5 Центральная предельная теорема
- •2.13 Марковские цепи
- •2.13.2 Марковские цепи
- •2.13.3 Пуассоновский процесс
- •Приложения
2.9 Числовые характеристики случайной величины (продолжение). Моменты
Рассмотрим два вида моментов – начальные и центральные.
Начальным
моментом
порядка k
случайной величины X
называют математическое ожидание для
случайной величины
![]() :
:
k=M(Xk), где k R. (2.46)
При k=1 имеем первый начальный момент 1=MX=m, который, как известно, есть математическое ожидание случайной величины X.
Отклонение для случайной величины X от своего математического ожидания X–MX называется центрированной случайной величиной X. Центрирование случайной величины аналогично переносу начала координат в среднюю точку – центр распределения.
Центральным моментом порядка k для случайной величины X называется математическое ожидание степени k соответствующей центрированной случайной величины X:
![]() ,
где k
R (2.47)
,
где k
R (2.47)
Можно доказать, что зависимость между начальным и центральным моментом порядка s выражается формулами:
![]()
![]()
![]()
![]() и
т.д.
и
т.д.
В связи с их особой ролью в исследованиях методами математической статистики, ограничимся рассмотрением первых четырех центральных моментов:
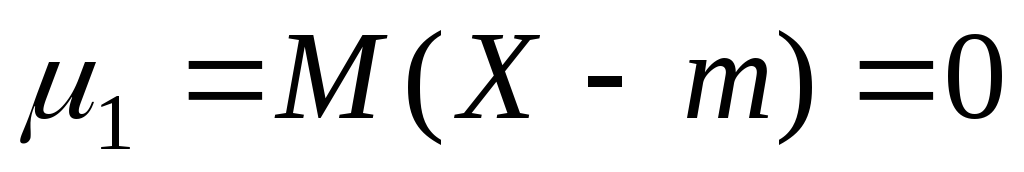 –есть
математическое
ожидание центрированной
случайной
величины X
или первый
центральный
момент;
–есть
математическое
ожидание центрированной
случайной
величины X
или первый
центральный
момент;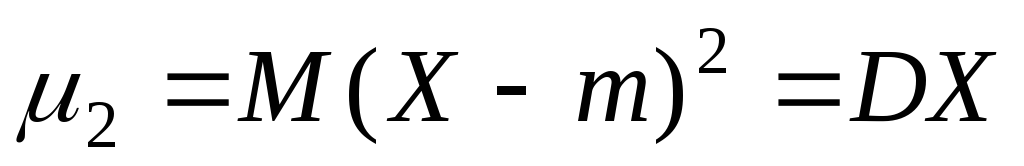 –есть
дисперсия
случайной величины X
или второй центральный момент;
–есть
дисперсия
случайной величины X
или второй центральный момент; –третий
центральный момент;
–третий
центральный момент;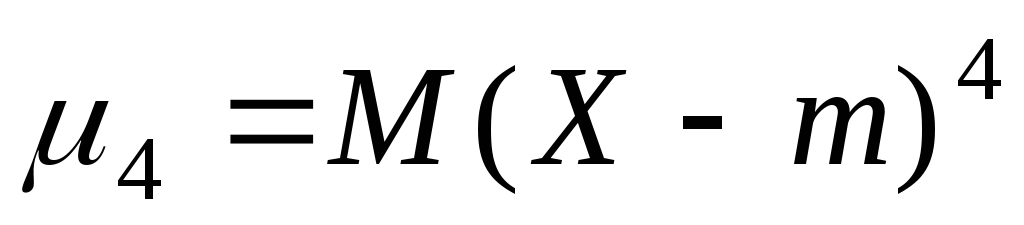 –четвертый
центральный момент.
–четвертый
центральный момент.
Моменты зависят от характера распределения СВ. Формулы, по которым они вычисляются для ДСВ и НСВ, сведем в таблице.
|
Виды моментов |
Виды распределений | |
|
ДСВ |
НСВ | |
|
Начальный момент порядка k |
|
|
|
Центральный момент порядка k |
|
|
«Центром»,
относительно которого вычисляется
центральный момент, служит первый
начальный момент
![]() ,
причем, суммирование выполняется по
всем принимаемым значениям, интегрирование
– по всей области определения.
,
причем, суммирование выполняется по
всем принимаемым значениям, интегрирование
– по всей области определения.
Моменты как характеристики распределения, дают дополнительную информацию об исследуемом распределении. Так, математическое ожидание – первый начальный момент – это средняя точка распределения, тот «центр», вокруг которого и вычисляются центральные моменты. Дисперсия – второй центральный момент – характеризует разброс вокруг математического ожидания. Третий центральный момент, деленный на третью степень среднеквадратического отклонения, есть асимметрия распределения:
![]() . (2.48)
. (2.48)
Если, распределение симметрично относительно своего центра, то A=0.
Четвертый центральный момент, деленный на четвертую степень среднего квадратического отклонения – эксцесс – характеризует «плосковершинность» распределения и вычисляется по формуле:
![]() . (2.49)
. (2.49)
Т.к.
для нормального распределения
![]() ,
тоE=0.
Для распределений, близких к нормальному,
отличный от нуля эксцесс показывает
степень различия между имеющимся
распределением и нормальным. Если
,
тоE=0.
Для распределений, близких к нормальному,
отличный от нуля эксцесс показывает
степень различия между имеющимся
распределением и нормальным. Если
![]() ,
то
кривая
распределений имеет более
,
то
кривая
распределений имеет более
![]() вершину.
вершину.
Значения асимметрии и эксцесса для различных распределений представим в таблице:
|
Вид распределения |
Асимметрия |
Эксцесс |
|
Нормальное XN(m, ) |
A=0 |
E=0 |
|
Равномерное XU(a, b) |
A=0 |
E= 1.2 |
|
Показательное XE() |
A=2 |
E=6 |
|
Биномиальное XBi(n, p) |
|
|
|
Геометрическое XG(p) |
A= |
E= |
|
Пуассона XП() |
|
|
