1.11 Локальная и интегральная теоремы Муавра-Лапласа

На практике часто возникает потребность вычислять вероятность Р_n(m) при достаточно больших значениях параметров.

Задача 31. Вероятность выхода из строя кодового замка в течение месяца равна 2%. Какова вероятность, что в партии из 600 кодовых замков, установленных фирмой на входных дверях домов, 20 кодовых замков выйдут из строя в течение месяца?

Решение. По условию n=600; m=20, p=0.02, q=0.98. Если применять формулу Бернулли,, то подсчет вероятности будет весьма сложен.

В таких случаях применяют «локальную приближенную формулу Муавра-Лапласа».

Локальная формула Муавра-Лапласа. Если в n независимых испытаниях событие A происходит с постоянной вероятностью р, которая не очень близка к 0 и 1, то при достаточном большом количестве испытаний вероятность того, что событие A произойдет m раз, приближенно равна

, (1.18)

где ,.

Причем, для функции (x) составлена таблица ее значений, которая публикуется в справочной литературе (Табл. 2 Приложений).

Тогда задача 31 может быть решена с помощью локальной формулы Муавра-Лапласа. При n=600, m=20, p=0.02, q=0.98 найдем:

1) .

2) .

4. Значение функции (x)= 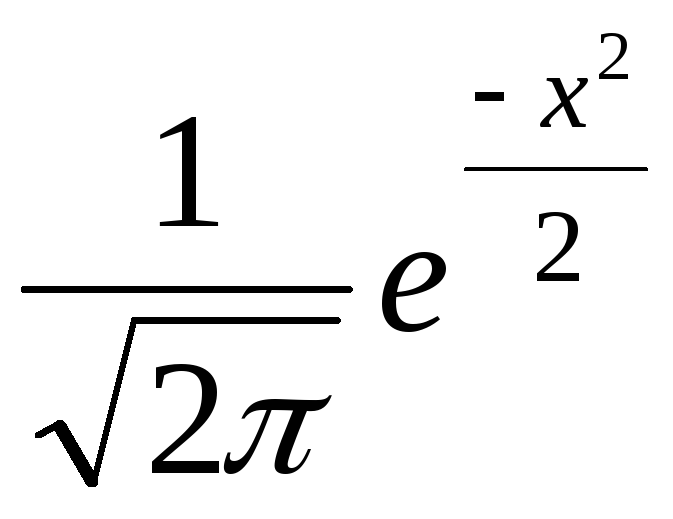для x=2.33 найдем из таблицы (Табл. 2 Приложений):

(2.33)

Тогда искомая вероятность Р₆₀₀(20) равна

.

Свойства локальной формулы Муавра-Лапласа:

1. функция (x) – четная;

2. x=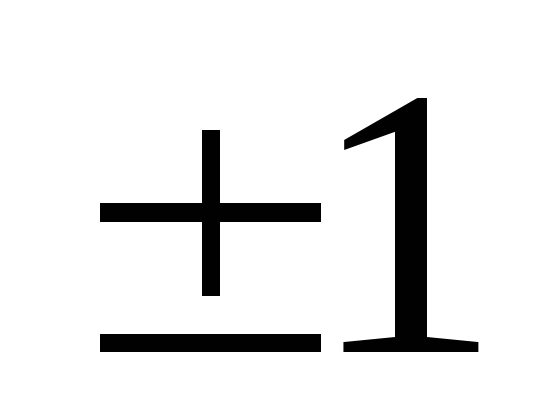– точки перегиба графика функции;

3. таблица значений функции (x) составлена для 0x5, т.к. при x5, (x)0;

4. формула применяется при npq10.

Интегральная формула Лапласа. Пусть требуется найти вероятность суммы 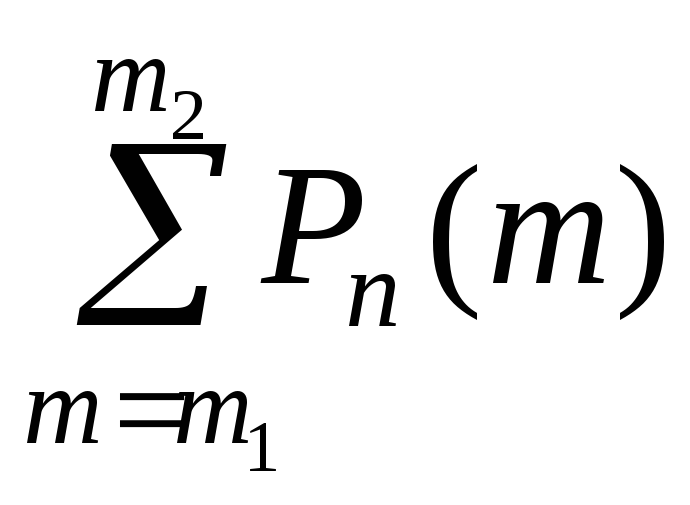на некотором интервале [m₁, m₂]. Для подсчета такой вероятности применяют интегральную формулу Лапласа.

Если в n независимых испытаниях событие A происходит с постоянной вероятностью р, которая отличается от 0 и 1, то при достаточно большом значении n вероятность того, что частота m события A находится в интервале [m₁,m₂], приближенно равна

Р_n(m₁  m  т₂)Ф(х₂)Ф(х₁), (1.19)

где 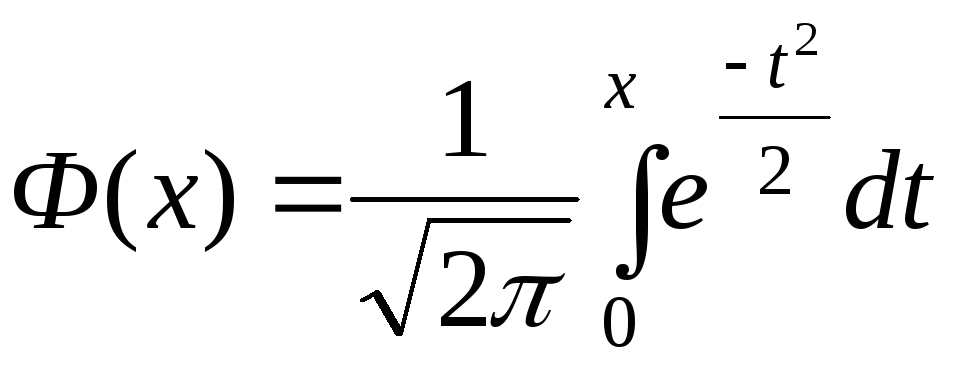, (1.20)

причем .

Функция Ф(x) является первообразной функции (x)= из локальной формулы Муавра-Лапласа и называется функцией (интегралом) Лапласа. Она принимает значения в интервале (0.5; 0.5), причем Ф(x)=Ф(x) – т.е. функция Лапласа  нечетная, Ф(+)=0.5, Ф(0)=0.

Задача 32. В каждом из 700 независимых испытаний на брак, появление стандартной лампочки происходит с постоянной вероятностью 0.65. Найти вероятность того, что при таких условиях, появление бракованной лампочки произойдет чаще, чем в 230 испытаниях, но реже, чем в 270 случаях.

Решение. Событие A  появление бракованной лампочки; по условию задачи n=700, p=10.65=0.35, q=0.65. Найти Р₇₀₀(230<m<270), если m₁=230, m₂=270. Применим интегральную формулу Лапласа:

1. .

2. х₁=,х₂=.

3. Значения функции Ф(x) при 1.19 и х₂=1.98 находим из таблиц (Табл. 3 Приложений).:

Ф(х₁)=Ф(1.19)Ф(1.19)0.383,

Ф(х₂) Ф(1.98)0.476.

4. Искомая вероятность

Р₇₀₀(230<m<270)Ф(х₂)Ф(х₁)0.476+0.3830.859.

Задача 33. В каждом из 500 независимых испытаний на всхожесть, событие A  прорастание исследуемого семени  происходит с постоянной вероятностью 0.4. Найти вероятность того, что среди 500 посаженных семян взойдет меньше 235.

Решение. По условию задачи n=500, p=0.4, m₁=0, m₂=235, q=10.4=0.6. Найти: Р₅₀₀(m<235).

1. .

2. х₁=,х₂=.

3. Ф(х₁)Ф(18)Ф(18) 0.5; Ф(х₂) Ф(3.18) 0.499.

4. Р₅₀₀( m<235)=Р₅₀₀ (0<m<235)Ф(х₂)Ф(х₁) 0.499(0.5)=0.999.

В таблице 3 даны значения функции Ф(x) только до лишь до x=5, т.к. для любых x5 функция Ф(x) принимает все значения Ф(x)=0.5.

Задача 34. Прибор выходит из строя при отказе (неисправности) его микросхемы. Вероятность отказа в речение одного часа работы прибора 0.02. С какой вероятностью за 100 часов эксплуатации прибора микросхему придется менять три раза?

Решение. По условию задачи: p=0.02, n=100, m=3, q=0.98. Тогда =np=1000.02=2<10, поэтому применим формулу Пуассона для редких явлений: , и, воспользовавшись таблицей 1, сразу получим приближенный ответ:

P₁₀₀(3)  P(3; 2)  0.18045  0.18.

Сравним этот ответ с ответом при использовании формулы Лапласа:

.

Тогда значение (x)  (0.714)0.31  найдем по таблице 2. Отсюда:

.

Разница в значениях вероятности связана с различиями в условиях применения формул Пуассона и Лапласа. Формула Лапласа обычно применяется при np >10, и поэтому она дала менее точный результат.

Приближенная формула гарантирует только малую абсолютную погрешность |x| =x , а относительная погрешность может быть сколь угодно велика.