2.12.5 Центральная предельная теорема

В теории вероятностей известна большая группа утверждений, объединенных названием: «Центральные предельные теоремы». Смысл этих теорем: при достаточно общих условиях, налагаемых на независимые случайные величины, функция распределения суммы n независимых случайных величин (или нормированной суммы) сходится по вероятности к нормальной функции распределения при n.

Теорема 1. Если Х₁, Х₂, …, Х_n – независимые случайные величины, распределенные одинаково, то в пределе при n функция распределения случайной величины неограниченно приближается к нормальной функции распределения.

Теорема 2. Если Х₁, Х₂, …, Х_n – независимые случайные величины, распределенные одинаково и имеющие математическое ожидание m и дисперсию  ², то в пределе при n функция распределения случайной величины неограниченно приближается к нормальной функции распределения:

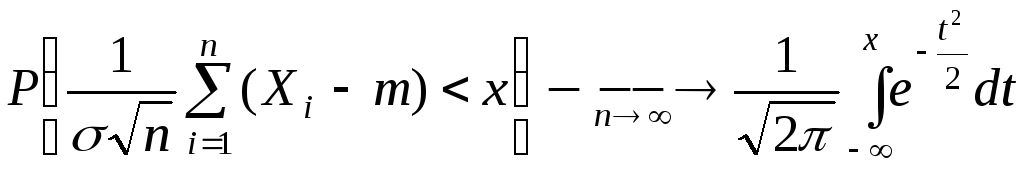. (2.67)

Закон больших чисел позволяет теоретически обосновывать устойчивость, т.е. практически - неслучайность основных эмпирических характеристик случайных величин: выборочных математического ожидания и дисперсии, асимметрии, эксцесса, выборочной функций распределения и т.д.

Пусть для изучения некоторого явления проводится серия экспериментов, порождающих случайную величину X. В первом эксперименте случайная величина X приняла значение x₁ , во втором – x₂,…, в n-ом – x_n.

Такие наблюдения (x₁, x₂, …, x_n) образуют выборку, представляющую собой независимые и одинаково распределённые случайные величины. Тогда к ним применимы теоремы Чебышева и Бернулли, с помощью которых можно обосновать статистическую устойчивость основных выборочных характеристик.

2.13 Марковские цепи

2.13.1 Понятие случайного процесса

Функцию X(t) называют случайной, если ее значения при любом аргументе t являются случайной величиной.

Случайным процессом называется случайная функция X(t), аргумент которой будем называть временем.

Рассмотрим некоторую систему, в которой протекает изучаемый случайный процесс. Назовем состоянием системы (состоянием случайного процесса) возможные значения случайных величин, образующих этот случайный процесс. Под испытаниями системы будем понимать изменения ее состояний. Процесс перехода системы из одного состояния в другое, протекающий случайным образом, является случайным процессом. Т.о., случайный процесс есть семейство случайных величин, заданных на одном и том же пространстве элементарных событий , зависящих от параметра t.

Частным видом случайных процессов являются марковские процессы, позволяющие описывать поведение разнообразных систем.

Случайный процесс, протекающий в некоторой системе, называют марковским процессом, если он обладает характерным свойством: для каждого фиксированного момента времени t₀ вероятность любого состояния системы в будущем (при t>t₀) зависит только от ее состояния в настоящем (при t=t₀) и не зависит от того, как развивался этот процесс в прошлом. Т.о., в марковских процессах не имеет значение «предыстория» модели, а существенно лишь ее нынешнее состояние.

В зависимости от характера множества значений функции X(t) и переменной t, различают отдельные виды случайных процессов:

– с дискретным состоянием и дискретным временем (цепь Маркова);

– с дискретным состоянием и непрерывным временем (непрерывная цепь Маркова);

– с непрерывным состоянием и дискретным временем (марковские последовательности);

– с непрерывным состоянием и непрерывным временем.