2.12.3 Теорема Чебышева

Если Х₁, Х₂, … , Х_n – последовательность попарно независимых СВ, имеющих конечные математическое ожидание и дисперсию, ограниченную некоторой постоянной величиной C: D(X₁)≤C, D(X₂)≤C, …, D(X_n)≤C,…, то среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий

, или для любого  >0,

.

Пусть Х₁, Х₂, … , Х_n – последовательность независимых СВ, имеющих конечные математическое ожидание и дисперсию, ограниченную некоторой постоянной величиной C. Тогда используем неравенство Чебышева для оценки вероятности отклонения среднего значения СВ от среднего значения их математического ожидания. Это значит, что для любого  >0 справедливо утверждение:

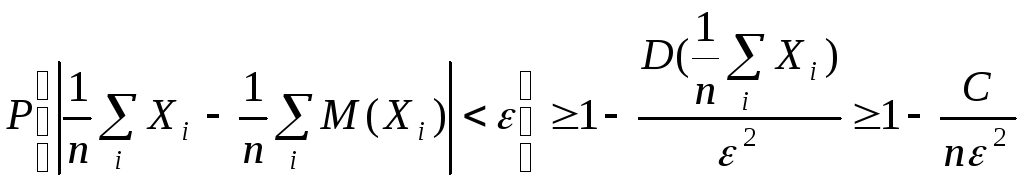. (2.62)

Действительно, если в неравенстве Чебышева учесть, что i имеет место неравенство D(Xi)≤C и, значит D(Xi)≤nC, то

.

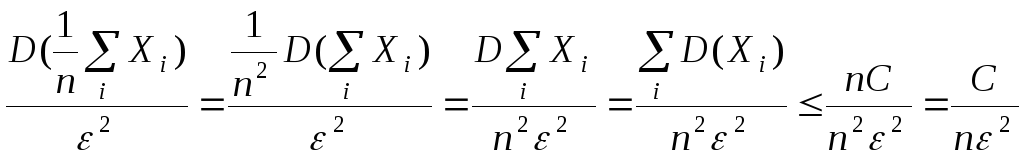Переходя к пределу при n, имеем .

Но т.К. Вероятность не превышает единицы, то справедливо

.

Это означает, что среднее арифметическое случайных величин Х₁, Х₂,…, Х_n, при n мало отличается от среднего арифметического их математических ожиданий M(X₁), M(X₂), …, M(X_n), т.е. обладает свойством устойчивости.

Для одинаково распределенных случайных величин с конечной дисперсией D обозначим математическое ожидание M(x_i)=m. Тогда теорема Чебышева принимает более простой вид:

. (2.63)

В математической статистике теорема Чебышева обосновывает тот самый выборочный метод, который дает возможность по характеристикам выборки изучать всю генеральную совокупность (п. 3.1).

Задача 21. Для определения средней продолжительности горения лампы в партии из 200 одинаковых ящиков взяли выбор по 1 лампочке из каждого ящика. Оценить вероятность того, что продолжительность горения выборки (200 ламп) отличается от средней продолжительности горения всех ламп (партии) по модулю меньше, чем на 5ч., если по ГОСТу стандартное отклонение не превышает 7ч.

Решение: Пусть X_i – продолжительность горения электролампы, взятой из i-го ящика, т.к. 7ч, D_i=(7ч)² = 49ч²=C.

Общая средняя продолжительность горения в выборке – (х₁+х₂+…+х₂₀₀)/200. Средняя продолжительность горения одной лампы в партии m=(Mх₁+Mх₂+…M+х₂₀₀)/200. Оценим снизу вероятность .

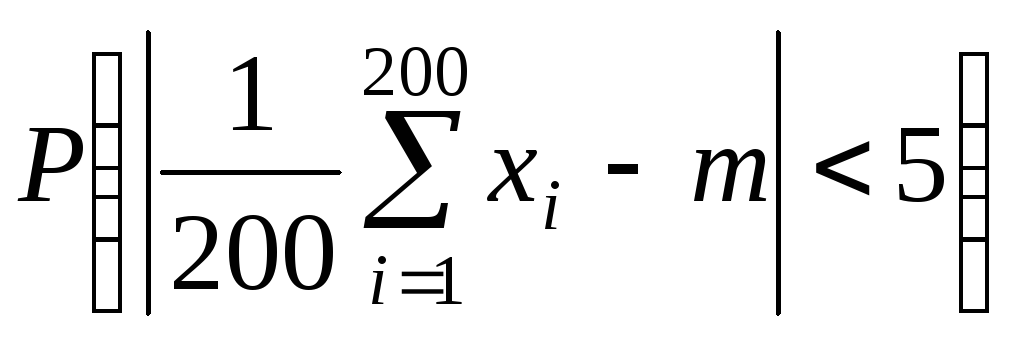Поскольку лампы стандартные, поэтому по теореме Чебышева со значениями параметров C=49ч²,  =5ч, n=200 получаем:

Р149ч²/2005² = 10.0098= 0.9902.

Задача 22. Сколько раз надо измерить данную величину, истинное значение которой а, чтобы с вероятностью Р0.95 можно было утверждать, что среднее арифметическое значение этих измерений отличается от а по модулю меньше чем 2, если прибор позволяет измерять со средним квадратичным отклонением меньше10?

Решение: Пусть X_i результат измерения i, по условию D(x)<10²=C. Тогда надо найти n, при котором Р (|(x₁+…+x_n)/n–a|<2) 0.95.

Т.к., где C=100,  =2, то

1-100/4n0.95, .

Т.о., надо произвести минимум 500 измерений.

2.12.4 Теорема Бернулли

Теорема Бернулли является частным случаем теоремы Чебышева.

Пусть вероятность успеха некоторого события A из серии n независимых повторных испытаний равна P(A)=p, среди которых m  число успешных испытаний, тогда для любого  > 0 имеет место предел

.

Доказательство. Оценим вероятность того, что отклонение числа m появления события в n испытаниях от математического ожидания не превосходит некоторого  >0. Т.к. испытания независимы, то ДСВ X подчиняется закону распределения Бернулли и имеет числовые характеристики: MX=np, DX=np()=npq.

Рассмотрим другую величину Y=X/n, имеющую соответственно характеристики:

MY=M(X/n)=1/n(X)=p;

D(Y)=D(X/n)=1/n²(X)=pq/n.

Применим неравенство Чебышева для ДСВ Y . Тогда

или . (2.64)

При увеличении числа экспериментов (n) величина вероятности отклонения частоты от математического ожидания стремится к нулю:

, а для противоположного события

. (2.65)

Эти записи являются разными формами записи теорема Бернулли. Переходя к пределу, имеем .

Задача 23. Из 1000 микрокалькуляторов, поступивших на базу, 200 было реализовано. Среди этих 200 микрокалькуляторов оказалось 25 бракованных. По этим данным как по случайной выборке определить вероятность того, что во всей партии бракованных микрокалькуляторов окажется не более 15% и не менее 10%.

Решение: 1) Найдем статистическую вероятность (частоту) бракованных микрокалькуляторов: .

2. Найдем наибольшее отклонение частоты появления бракованных микрокалькуляторов от вероятности по модулю, если число :.

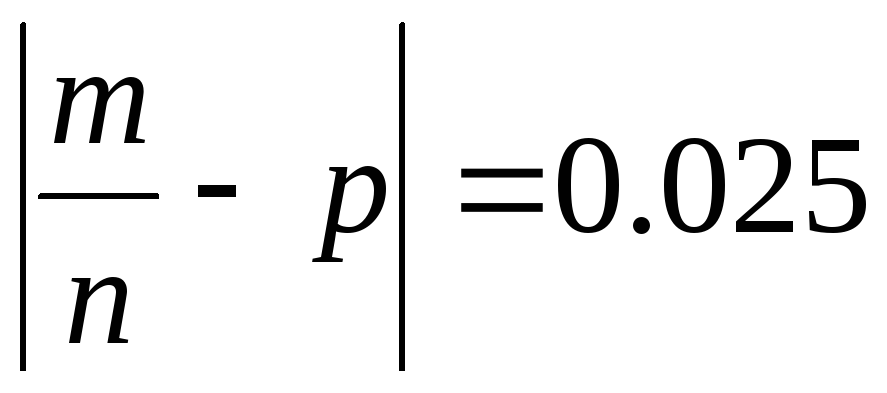3. Найдем искомую вероятность по формуле

.

Тогда .

То есть с вероятностью, большей, чем 0.825, можно утверждать, что бракованных микрокалькуляторов будет от 10% до 15%.

Теорема Бернулли означает, что относительная частота числа успехов m в n испытаниях Бернулли обладает свойством статистической устойчивости, то есть мало отличается от вероятности, полученной с помощью расчетов. На этом свойстве основаны надежность доверительных оценок вероятности в математической статистике.

Эта теорема дает возможность использовать известные формулы для расчета числовых характеристик СВ и применять соответствующие таблицы (функции Лапласа). А так как действие множества различных других законов распределения, при их неограниченном увеличении, так же подчиняется закону нормального распределения, то центральная предельная теорема приобретает широкое практическое значение. Благодаря выводу из этой теоремы, для взаимно независимых СВ при можно найти числовые характеристики по формулам, соответствующим данному виду распределений, а оценивать вероятность их суммарное действие по формулам, соответствующим закону нормального распределения (через функцию Лапласа).

Пусть повторные испытания происходят с постоянной вероятностью p. Найти вероятность выполнения неравенства , то есть в серии изn испытаний частота m/n отличается по модулю от вероятности не более чем на .

Итак, надо найти значение вероятности . Из неравенстваимеем. Умножая на, тогда:

.

Используя интегральную теорему Лапласа и нечетность функций Лапласа Ф(x)= Ф(x), имеем

. (2.66)

Задача 24. Вероятность появления нестандартного элемента питания равна 0,05. Найти вероятность того, что среди случайно отобранных 500 батареек относительная частота появления нестандартной батарейки отклонится от вероятности не более чем на 0,03.

Решение: По условию задачи имеем ,,. Тогда.

Оценим неизвестную вероятность по формуле:

.

Тогда .

По таблицам 3 приложений найдем значение , тогда.

Задача 25. (Опыт Бюффона). Один из первых математиков, изучавших вероятности событий, француз Бюффон (XVIII век), для выявления действия «Закона больших чисел» подбрасывал монету 4040 раз, причем герб появлялся в 2048 случаях.

Найти вероятность того, что при повторении опыта Бюффона, относительная частота появления герба отклонится от вероятности по модулю не более чем в опыте Бюффона.

Решение: По условию задачи относительная частота появления герба в опыте Бюффона , где,, а теоретическая вероятность появления гербаp=1/2. Тогда оценим

или

.

Полученный результат еще раз показывает, что для большей уверенности в результатах нужно проводить большее число независимых испытаний.

Действительно, в истории науки известны результаты английского статистика Пирсона по подсчету числа выпадения герба в опытах с монетой. Сравним их с результатами опыта Бюффона:

Опыты	Число испытаний	Относительная частота	Отклонение относительной частоты от вероятности
Опыт Бюффона	4040	0.5069	0.0069
Первый опыт Пирсона	12000	0.5016	0.0016
Второй опыт Пирсона	24000	0.5005	0.0005

Эти опыты служат эмпирическим доказательством теоретического вывода о существовании статистической устойчивости частот как уникального свойства случайных событий.

Задача 26. На опытном участке посажено 1000 семян пшеницы с вероятностью прорастания каждого семени p=0.9. Оценить отклонение частоты всхожести семян от их вероятности при вероятности этого события P=0.995.

Решение: Пусть n=1000 – число независимых испытаний, A – событие, состоящее в том, что модуль отклонений частоты всхожести семян от их вероятности не превышает некоторого числа . Найдем это число:

Итак, , где.

Тогда

или .

По таблице функции Лапласа Ф(x) найдем соответствующее значение x. Получаем соотношение , откуда и найдем значение:

.

Этот ответ означает, что с вероятностью 0.995 частота прорастания семян отличается от вероятности по модулю на 0.027.

Задача 27. Вероятность появления события в каждом из независимых испытаний равна 0.5. Найти число испытаний n, при котором с вероятностью 0.7698 можно ожидать, что относительная частота появления события отклонится от его вероятности по модулю меньше, чем на 0.02.

Решение: p=0.5, q=0.5, =0.02,

.

Отсюда ; по таблицам функции Лапласа находим аргумент, где значение функции Лапласа наиболее близко к 0.3949. Тогда . Отсюдаn=900.