2.5 Непрерывные случайные величины и их числовые характеристики
Итак, функция распределения ДСВ изменяется скачкообразно и выражает, например, количество взошедших семян, бракованных изделий, попаданий в мишень и т.д. Но может оказаться, что функция распределения изменяется непрерывно и вообще не имеет скачков: рост или вес ребенка как функция времени, напряжение электрического тока в городской сети, поломка электроприборов и т.д. В таком случае случайная величина принимает не только отдельные определенные значения, но и все действительные значения в интервалах между ними.
2.5.1 Плотность распределения вероятностей
Случайная
величина
называется непрерывной,
если функция ее распределения
,x
R,
представима в виде
, (2.21)
т.е. является непрерывной кусочно-дифференцируемой функцией с непрерывной производной.
Каждому промежутку (a;b) из области значений непрерывной случайной величины (НСВ) соответствует определенная вероятность P(ax<b) того, что значение этой случайной величины попало в указанный полуинтервал.
На промежутке (a;b) невозможно перечислить все значения случайной величины, т.к. множество его точек несчетно, но можно утверждать, что вероятность каждого отдельно взятого значения НСВ есть бесконечно малая величина (из геометрического определения вероятности). Поэтому для НСВ имеет смысл говорить о вероятности не конкретного значения, а попадания в некий интервал значений.
Свойства функции распределения НСВ
1) Функция распределения непрерывна на R как функция верхнего предела в несобственном интеграле с «закрепленным», хотя и бесконечным, нижним пределом.
2)
,
но т.к. >0
Рx=b}<
для НСВ,
то
. (2.22)
Свойства плотности вероятности f(x)
1)
. (2.23)
Эта формула, также как и определение функции распределения, устанавливает связь между функцией распределения и плотностью вероятности.
2) f(x) определена почти всюду (множество К точек, где функция распределения не дифференцируема, не более, чем счетно).
3) f(x)0, т.к. F(x) неубывающая функция.
4) f(x) интегрируема на R.
5) функция распределения есть та первообразная плотности вероятности, что обращается в ноль на бесконечности.
6)
как вероятность достоверного события.
вероятность нахождения величины в интервале ab равна
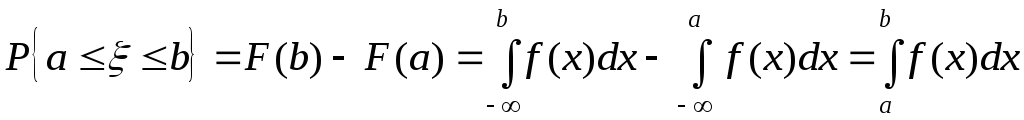(2.24)
(по формуле Ньютона-Лейбница).
Закон распределения НСВ принято задавать с помощью функции плотности вероятности f(x), так как функция распределения F(x) не всегда выражается в элементарных функциях.
2.5.2 Числовые характеристики непрерывной случайной величины
К основным числовым характеристикам непрерывной случайной величины относятся мода, медиана, математическое ожидание, дисперсия и среднеквадратическое отклонение.
Модой непрерывной случайной величины X называется такое ее значение, при котором плотность вероятности максимальная. Случайная величина может иметь несколько мод.
Обозначается мода М или Мо. С геометрической точки зрения мода – значение аргумента x, при котором график функции плотности распределения принимает максимальное значение.
Нахождение моды известная задача дифференциального исчисления поиска экстремума на множестве. Если функция f(x) дифференцируема на интервале, то ищутся “подозрительные” на локальный экстремум точки {x0i}, а из них выбирается max f(x0i), который нужно сравнить со значениями f(x) на границах интервала.
Медианой Me непрерывной случайной величины x называется такое ее значение , для которого равновероятно, что случайная величина x больше или меньше :
P(X<)=P(X>)=1/2.
В случае, когда ось симметрии кривой распределения y=f(x) совпадает с прямой x=m, то выполняется соотношение равной вероятности для x= в точке m, и тогда Me==m.
В
общем случае медиана есть корень
алгебраического уравнения F(x)=1/2
или интегрального уравнения
.
С геометрической точки зрения медиана делит площадь под графиком функции плотности вероятности на две равные части.
Математическим ожиданием непрерывной случайной величины называется интеграл
. (2.25)
Для функции от НСВ справедливо утверждение, что она распределена так же, как и сама НСВ. Поэтому математическим ожиданием функции G от НСВ X называется интеграл
. (2.26)
С геометрической точки зрения математическое ожидание случайной величины равно абсциссе центра тяжести площади, ограниченной кривой распределения и осью абсцисс. В рассматриваемом случае, когда кривая распределения симметрична относительно прямой x=m, математическое ожидание также совпадает с этой абсциссой. Тогда математическое ожидание, мода и медиана равны между собой:
m=М(X)=Me=.
Дисперсия непрерывной случайной величины X находится по формуле
. (2.27)
Дисперсия характеризует степень рассеяния значений случайной величины от своего среднего значения. Все свойства математического ожидания и дисперсии, сформулированные для ДСВ, сохраняются и для НСВ. Как и для ДСВ, формула дисперсии имеет и другой вид:
. (2.28)
Задача 13. Плотность вероятности случайной величины X задана функцией распределения:
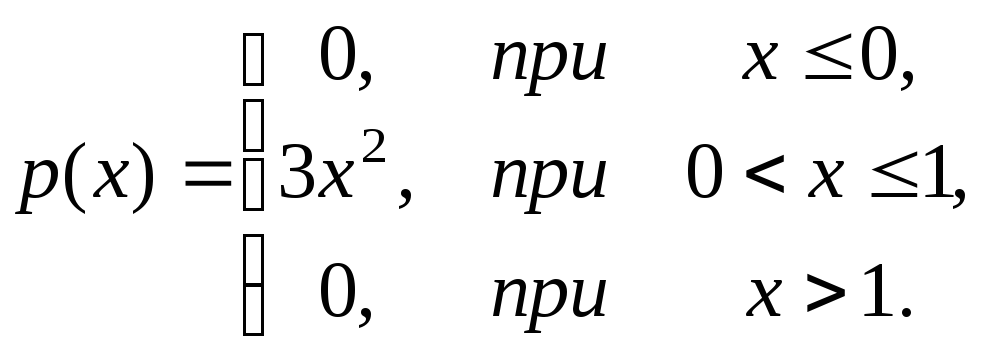
Найти:
Функцию распределения и ее график.
Числовые характеристики НСВ X.
Построить график плотности вероятности.
Найти вероятность попадания на интервал
.
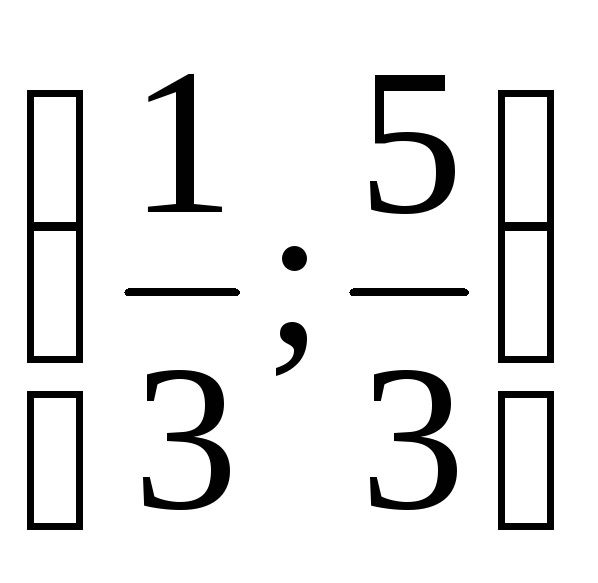Решение. 1. 
, т.е.
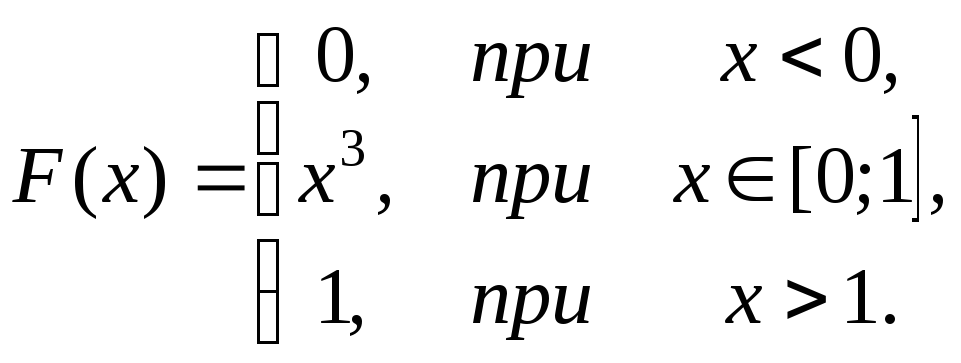
3. График функции распределения и график плотности вероятности имеют вид (рис.14):
f(x)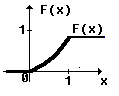
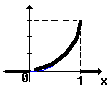
а) б)
Рис.14
Найдем числовые характеристики:
,
.
Мода
находится в процессе исследования на
экстремум плотности вероятности
по известному алгоритму, причем приx<0
и x>1
моды заведомо нет, т.к. отрицательная
плотность вероятности равна нулю.
Согласно алгоритму исследования на экстремум плотности вероятности выполним действия:
Найдем производную
.Приравняем производную к нулю и найдем критические точки: 6x=0, т.е. x=0. Следовательно, внутри интервала (0;1), где ПВ дифференцируема, моды нет.
Сравним значения ПВ в точках, где она не дифференцируема, т.е. при x=0 и x=1: р(0)=0, а р(1)=3. Следовательно, Мо(X)=3.
Для вычисления медианы решим уравнение F(x>)=F(x<)= 0.5: очевидно, его корень должен находиться в интервале (0;1) т.е.
.
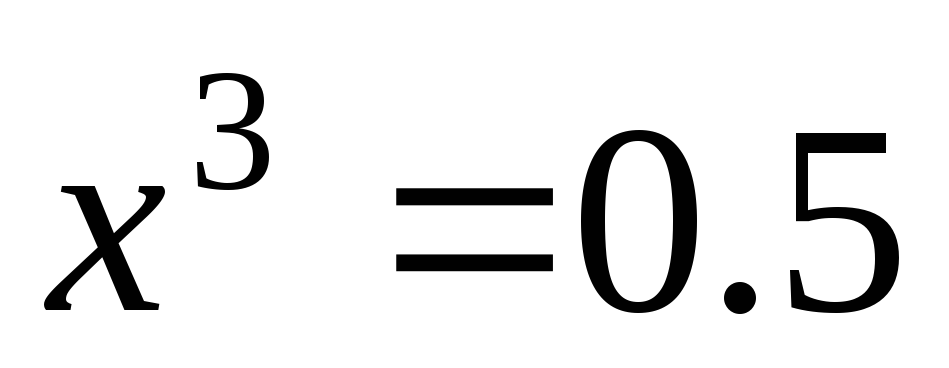Отсюда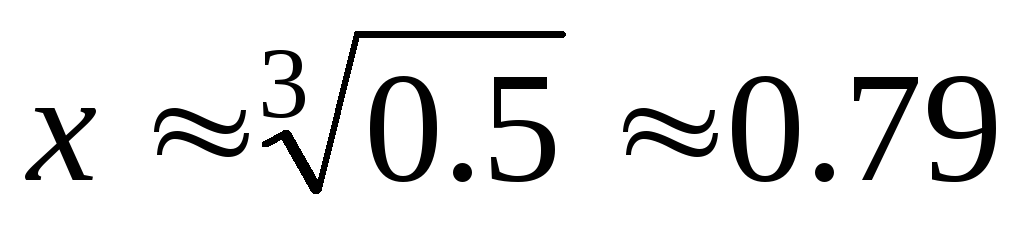
.
Поэтому медиана равнаМе(X)=0.79.
4. Вероятность
попадания случайной величины X
на интервале
находится с учетом, что
.
Тогда
.
К важнейшим непрерывным распределениям относятся нормальное, равномерное и показательное распределения.