1.4 Элементы комбинаторики

Комбинаторикой называется раздел математики, в котором решаются задачи на составление различных комбинаций из конечного числа элементов, подчиненных тем или иным условиям, и подсчет числа всех возможных таких комбинаций.

1) Правило суммы.

Обозначим число элементов конечного множества A через n(A). Если множества A и B конечны и A∩B = Ø, то n(AB)= n(A)+n(B).

На практике будем применять другой вариант правила суммы: если из некоторого множества элемент A можно выбрать k способами, а элемент B – m способами, причем любой способ выбора A отличается от любого способа выбора B, то выбор «A или B» можно сделать k+m способами.

Ключевое слово для применения правила суммы – слово или.

2) Правило произведения.

Если из некоторого множества элемент A можно выбрать k способами и после каждого такого выбора элемент B может быть выбран m способами, то упорядоченную пару (A,B) можно выбрать способами.

Т.к. в такое (декартово) произведение входят и элементы первого, и элементы второго множества, то при решении задач важно помнить ключевое слово и.

Назовем кортежем длины m из элементов множества A упорядоченную последовательность а₁, а₂,..., а_m  элементов этого множества.

Частным случаем правила произведения является число так называемых «размещений с повторениями» =m^k для подсчета кортежей длины k, составленных из m элементов множества X (среди которых могут быть повторяющиеся). Т.е., если n(X)=m, то .

Задача 5. В институте есть три варианта занятий по интересам: творческие объединения спортивные секции и научное студенческое общество. Каждое направление содержит по четыре вида коллективов: театральный, музыкальный, танцевальный и КВН – творческие коллективы, легкая атлетика, лыжи, спортивные игры и плавание – спортивные секции. В состав НСО входят естественно-математическое, гуманитарное, техническое и информационное объединения. Сколькими способами студенты могут разнообразить свой досуг в институте после занятий, выбрав одно занятие по интересам?

Решение. Пусть A – количество вариантов направлений по интересам, B – количество вариантов в каждом направлении.

Т.к. надо учесть и три основных направления – множество A, и то, что в каждом из них по четыре коллектива – множество B, то для подсчета общего числа вариантов применим правило произведения: n(A)=3, n(B)=4, тогда n(AB)= n(A) n(B)=34=12.

Задача 6. Сколько различных двоичных чисел длиною 6 можно записать с помощью цифр 0 и 1?

Решение. Размещаем две цифры (0, 1) на шесть возможных мест, т.е. на каждом из шести мест (n=6) может быть одна из двух двоичных цифр. А всех таких вариантов будет = 2⁶=64 двоичных чисел: на каждом из шести мест по два варианта цифр, т.е. шесть кортежей длины 2.

3) Перестановки.

Рассматривая различные подмножества множества X, состоящего из n элементов, выделим три принципиально разные задачи для подсчета числа элементов подмножеств:

1. Сколькими способами можно представлять элементы множества, чтобы получить различные кортежи длины n?

2. Сколькими способами из всего множества можно выбрать различные кортежи (упорядоченные подмножества) длиной m, (m<n)?

3. Сколькими способами из всего множества можно выбрать различные подмножества длиной m, (m<n)?

Для решения первой задачи необходимо найти число перестановок длины n.

Упорядоченные множества, состоящие из n элементов, т.е. кортежи длины n, называются перестановками (без повторений). Их число обозначается Р_n.

Формула перестановок имеет вид

P_n=n!, причем, P_n=n!=nP_n-1. (1.10)

Последняя формула называется рекуррентной и дает возможность подсчитывать число перестановок во множестве n+1 элемента через перестановки во множестве n элементов:

Заметим, что P₁=1!=1, а P₀=0!=1.

4) Размещения (без повторений).

Упорядоченное подмножество m элементов, т.е. кортеж длины m, составленное из всего множества, содержащего n элементов, называется размещением (без повторения). Полученные комбинации отличаются друг от друга либо составом элементов, либо их порядком. Число таких размещений обозначают или (n,m) и вычисляют по формуле:

. (1.11)

Задача 7. Сколькими способами из различных нечетных цифр можно составить различные трехзначные числа?

Решение. Нечетных цифр пять: 1, 3, 5, 7, 9, тогда количество различных трехзначных чисел найдем по формуле .

5) Сочетания (без повторений).

Сочетания из n элементов отличаются от размещений тем, что в подмножестве, состоящем из m элементов, для размещений порядок определен, а для сочетаний – не важен. Полученные комбинации отличаются друг от друга лишь составом элементов.

Поэтому сочетаниями из n элементов по m называется неупорядоченное подмножество, состоящее из m элементов, взятых из множества, состоящего из n элементов. Число таких сочетаний обозначается и вычисляется по формуле:

. (1.12)

При решении комбинаторных задач (без повторений) удобно использовать алгоритм (Рис.4), в котором необходимо найти ответы на два «ключевых» вопроса:

– во всем ли множестве необходимо найти число возможных вариантов?

– важен ли порядок расположения отдельных элементов в исследуемом множестве (подмножестве)?

Алгоритм решения комбинаторных задач:

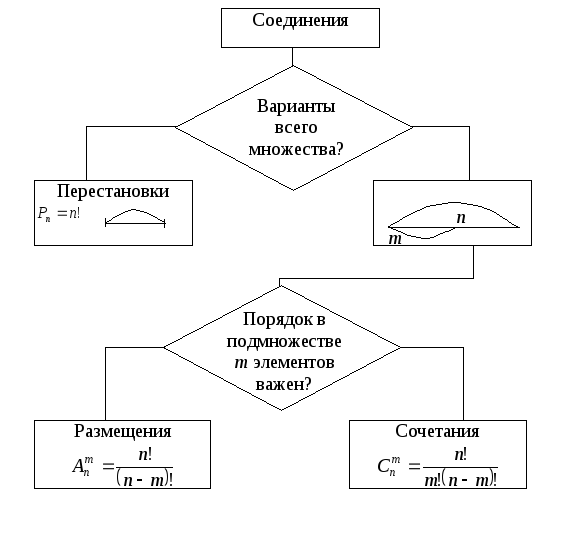
Рис.4

Задача 8. Сколькими способами могут пришвартоваться к причалу 3 судна, если в порт прибыло 7 кораблей?

Решение. По условию задачи из элементов всего множества (семи кораблей) надо найти число способов их объединить в подмножества по три элемента, т.е. :

.

Задача 9. Найти число точек пересечения диагоналей выпуклого n-угольника, если никакие три из них не пересекаются в одной точке.

Решение. Минимальный многоугольник с диагоналями имеет четыре вершины (n=4). Если взять любые 4 вершины многоугольника, то через них можно провести четыре диагонали, имеющие по две точки пересечения, но только одна из них лежит внутри многоугольника. Поставим этой точке пересечения диагоналей в соответствие четверку выбранных вершин многоугольника. Такое соответствие является взаимно однозначным, однако, порядок вершин не важен. Поэтому число внутренних точек пересечения диагоналей многоугольника (и число четверок-вершин) можно найти с помощью сочетаний .