2.6 Нормальное распределение и его числовые характеристики

Самым распространенным в природе, в экономике, социологии и других науках является нормальное распределение непрерывной случайной величины. С помощью нормального распределения можно описать плотность вероятности непрерывных случайных величин в тех случаях, когда отклонения от средней случайной величины появляются за счет различных явлений, воздействующих независимо одно от другого, но примерно в одинаковой степени, причем, чем больше суммируется таких случайных величин, тем результат точнее. Все эти явления не зависят друг от друга, но, воздействуя на процесс изготовления примерно с одинаковой силой, обуславливают то, что закон, по которому изменяется непрерывная случайная величина (размер конкретной детали), описывается нормальным распределением.

Самое точное изготовление детали с заданными размерами – “эталон” – будет соответствовать математическому ожиданию m, разброс фактических значений случайной величины размера детали будет соответствовать понятию дисперсии (точнее – среднеквадратическому отклонению).

Случайная величина с нормальным распределением существует в интервале (-; ) и описывается законами:

– плотности вероятности f(x), называемой «кривая Гаусса» (рис. 15а)

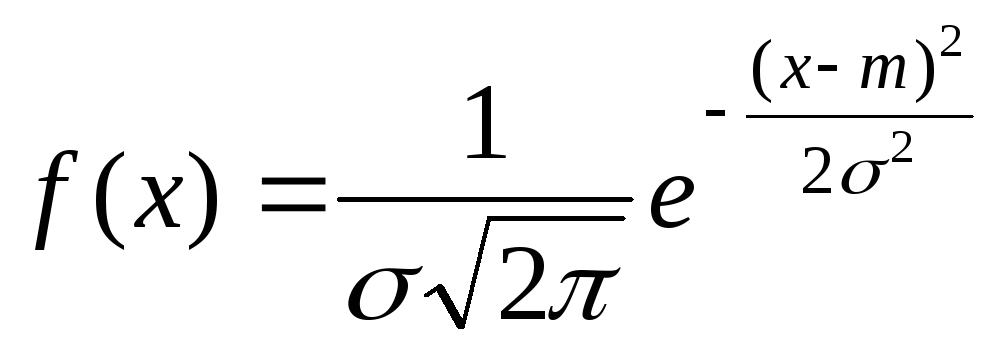, (2.29)

где  и m – параметры нормального распределения, причем  >0,

– функцией распределения F(x) (рис. 15б):

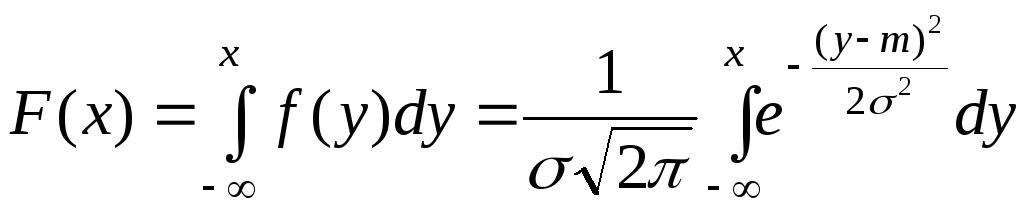. (2.30)

Подстановкой интеграл приводится к виду:

.

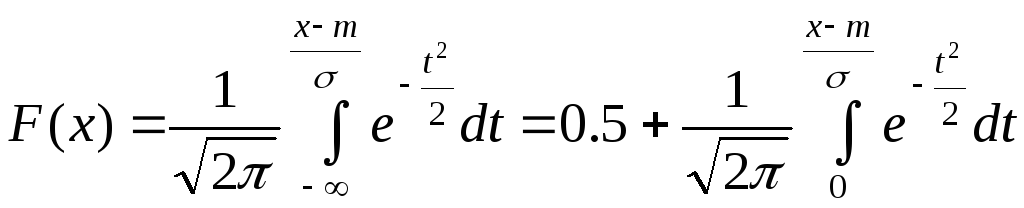Поэтому для удобства вводится нечетная функция 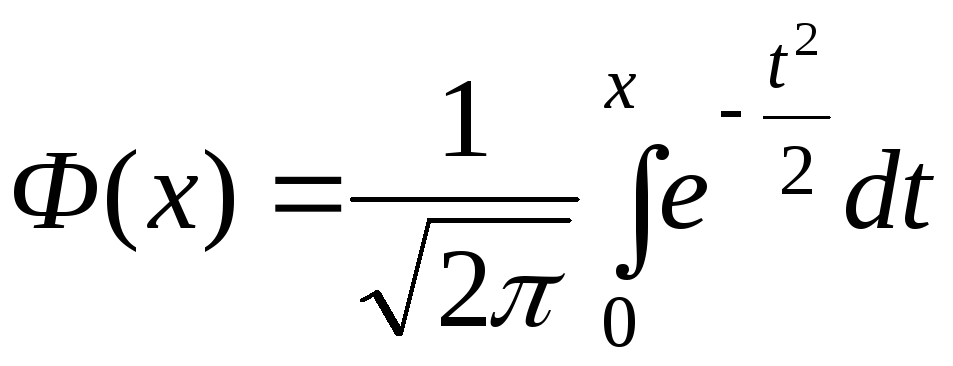, называемаяфункцией Лапласа. Функцию Лапласа называют также “интегралом вероятности” или “функцией ошибок”. Очевидно, что Ф(0)=0, Ф(+)=1/2, Ф(– x)= – Ф(x).

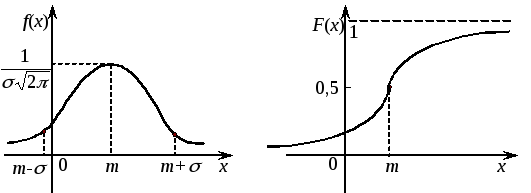
а) б)

Рис. 15

Математическое ожидание МХ случайной величины X, распределенной нормально, равно

, (2.31)

а дисперсия равна

, (2.32)

поэтому параметр  – есть среднеквадратическое отклонение.

Случайную величину X, распределенную нормально с параметрами  и m, обозначают XN(m,).

На практике для вычисления значений функции Лапласа используются специально составленные таблицы, которые приводятся в справочной литературе (Таблица 3 Приложений).

Вероятность попадания в интервал НСВ, распределенной по формульному закону, можно найти с помощью функции Лапласа по формуле:

Величины параметров нормального распределения СВ X непосредственно влияют на форму кривой : приона принимает свое максимальное значение, равное. Поэтому смаксимальная ординатаи кривая становится более пологой, приближаясь к осиОх.

Величина математического ожидания m влияет на расположение кривой относительно оси ординат: приm кривая смещается .

Поэтому с помощью подстановки можно получить функциюплотности вероятности, график которой симметричен относительно осиОу. Такая кривая соответствует нормированному закону нормального распределения с параметрами и, т.е.N(0,1). Его график имеет вид:

Величину XN(0,1) иногда называют стандартно нормальной. Ее функция распределения имеет вид (интеграл Лапласа, табл. 3 Приложений).

2.7 Равномерные распределения

Равномерным называется распределение таких случайных величин, все значения которых лежат на некотором отрезке a; b и имеют постоянную плотность вероятности на этом отрезке.

Плотность вероятности задается формулой:

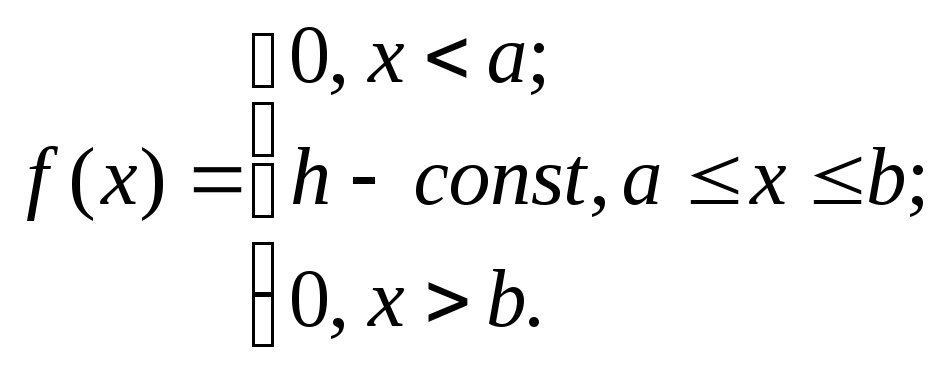(2.33)

При равномерном распределении график плотности вероятности имеет вид (рис.16):

0

Рис.16

Поскольку площадь прямоугольника равна (b–a)=1, то . Тогда функцию плотности вероятности можно записать в другом виде:

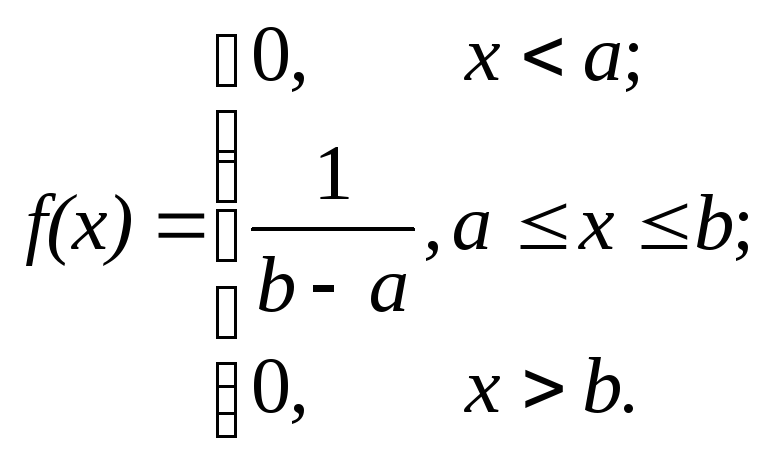(2.34)

Видно, что равномерное распределение задается указанием соответствующего отрезка, поэтому СВ X, распределенная равномерно на [a, b], обозначается XU[a, b] (от англ. uniform – равномерный).

Для равномерного распределения нельзя указать моду, так как все вероятности принимают одинаковые значения.

Математическое ожидание случайной величины при равномерном распределении равно

, (2.35)

т.е. среднему арифметическому концов отрезка: МX=.

Дисперсию равномерного распределения найдем по формуле

DX=М(X ²)М ²(X).

Действительно, М(X²)=. Тогда дисперсия равна:

. (2.36)

Среднеквадратическое отклонение

(X)= , (2.37)

(так как b>a по условию).

Случайные величины с равномерным распределением встречаются в тех случаях, когда по условиям эксперимента случайная величина X принимает значения в конечном промежутке a; b, причем все значения равновероятны:

– «X» – время ожидания автобуса на остановке (случайная величина x равномерно распределена на отрезке 0; b, где b – интервал движения между автобусами);

– «X» – ошибка при взвешивании некоторого предмета, полученная при округлении результата до целого значения (в этом случае x-0.5; 0.5), если цена деления шкалы весов равна единице) и др.

Функция распределения случайной величины, равномерно распределенной на отрезке a; b, имеет вид:

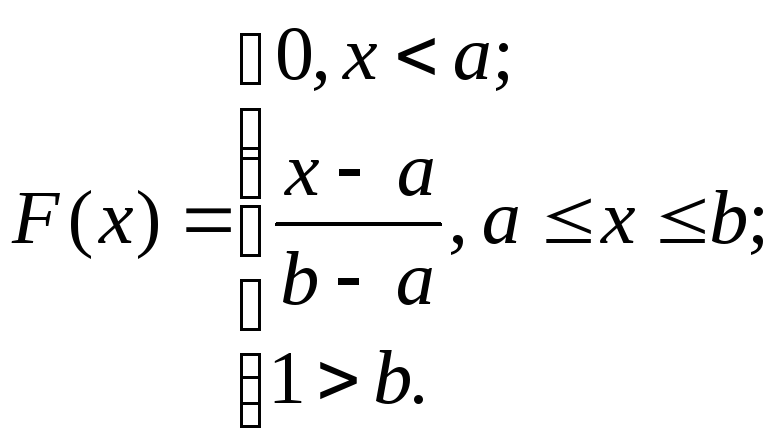(2.38)

Е

0

е график изображен на рис.17:

Рис.17

Если некоторый отрезок   длиной целиком содержится в отрезкеa; b, то вероятность попадания в него случайной величины XU[a, b], распределенной равномерно, находится по формуле

, (2.39)

где l – длина отрезка  . Это значит, что вероятность попадания в любую фиксированную область отрезка a; b пропорциональна длине этой области. Вероятность попадания в область   можно записать и в виде:

Р(x)=,

что соответствует геометрическому определению вероятности. Отсюда можно сделать вывод, что непрерывное равномерное распределение влечет за собой геометрические вероятности.

Задача 14. НСВ X задана функцией распределения

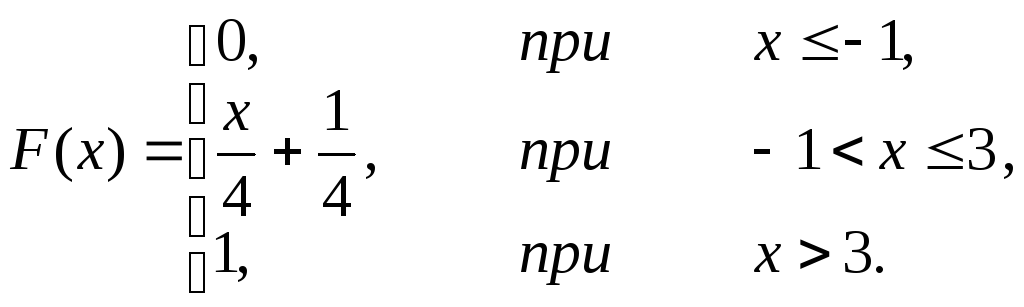
Найти:

1. Вероятность того, что в результате испытания X примет значение в интервале (0; 2).

2. Плотность вероятности f(x).

3. Числовые характеристики НСВ X.

Решение. 1. Найдем вероятность попадания значения X в интервал (0;2):

.

2. Плотность вероятности f(x)=: Поэтому, т.е.

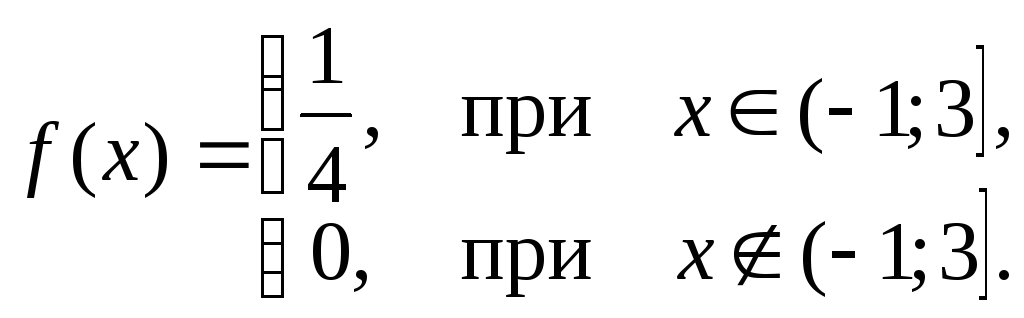
3. Математическое ожидание , т.е.

,

Тогда среднеквадратическое отклонение Для того чтобы найти моду, надо исследовать на экстремумf(x): т.к. , то моды нет.

По виду заданной плотности вероятности можно было сразу понять, что задана равномерно распределенная СВ. Тогда, очевидно, ее мода не существует, а математическое ожидание – МX=.

Для того чтобы найти медиану Me, надо решить уравнение . Тогда.

Медиану найдем из уравнения . Значит.

График функции распределения F(x) представлен на рис.18a, а плотность вероятности на рис.18б):

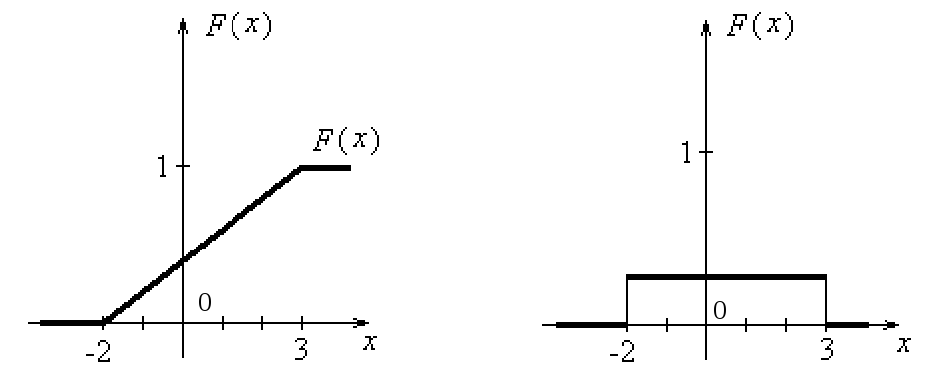
а) б)

Рис.18