
Navch._posibnuk_Ivaschyk
.pdf
T |
T |
T |
T T |
||
∑αj |
Kt− j = ∑αj ∑βτit− j−τ = ∑∑αjβτit− j−τ . (17.68) |
||||
j=1 |
j=1 τ=1 |
j=1 τ=1 |
|||
Оскільки праві частини (17.67) і (17.68) рівні, то рівні і їхні ліві |
|||||
частини, тобто: |
|
|
|
|
|
T |
T |
|
|
|
|
∑βj It− j = ∑αj |
Kt− j , t = |
|
. |
(17.69) |
|
1,T |
|||||
j=1 |
j=1 |
|
|
|
|
Рівняння (17.69) зв’язує між собою змінні Іt-j i Кt-j із різними значеннями лага j. Воно називається рівнянням загального (чи змішаного) розподіленого лага. Відповідно до цієї моделі приріст капіталу в t-му році пов'язаний із приростами капіталу та інвестиційними вкладеннями попередніх (Т–1) років і інвестиційними вкладеннями поточного року:
|
1 |
T |
T |
|
|
|
Kt = |
|
∑βj It− j+1 −∑αj |
Kt− j+1 |
. |
(17.70) |
|
|
||||||
|
αt j=1 |
j=1 |
|
|
|
|
Рівняння (17.70) можна розглядати як рівняння множинної лінійної регресії. Однак оцінювання його параметрів є трудомістким процесом. По-перше, число оцінюваних параметрів, яке тут становить 2Т, може бути досить великим. По-друге, повинна виконуватися
T |
T |
умова 0 ≤ αj ≤1;0 ≤ βj ≤1;∑αj =1;∑βj =1. Але автоматичне |
|
j=1 |
j=1 |
виконання цієї умови не є гарантованим. По-третє, рівняння (17.70) не містить вільного члена, що може погіршити якість оцінки. Почетверте, досить велика небезпека наявності мультиколінеарності. Через це рівняння (17.70) перетворюють, спрощують, а вже потім оцінюють. Розглянемо найбільш важливі часткові випадки моделі
(17.69-17.70).
Для двох часткових випадків загальної моделі розподіленого лага існують певні моделі стосовно структури коефіцієнтів {ατ} і {βτ}.
Модель L. Усі інвестиції для чергової групі об’єктів вкладаються на початковому етапі досліджуваного періоду, а прирости капіталу надалі розподілені на Т етапів (років), тобто
α1 =1,αj = 0, j = 2,T . Тоді модель (17.69) набуває вигляду:
T |
|
Kt = ∑βj It− j+1 . |
(17.71) |
j=1
Цю модель часто називають моделлю з ліворозподіленим лагом (L) через те, що в причинно-наслідковому співвідношенні ( I → K )
591
розподілена в часі його ліва частина. В співвідношенні з цією моделлю фіксовані частки {βj} інвестицій окресленого року t переходять у прирости капіталу даного та кожного наступного року.
Модель R. Увесь приріст капіталу для чергової групи проектів відбувається на завершальному етапі досліджуваного періоду;
інвестиції розподілені по Т етапах |
(роках), тобто |
βТ=1, βj=0, |
||
|
|
|
||
j =1,T −1. У цьому випадку модель (17.69) матиме вигляд: |
||||
|
|
T |
|
|
|
|
It = ∑αj |
Kt+T − j . |
(17.72) |
j=1
Таку модель називають моделлю з праворозподіленим лагом (R). В ній у причинно-наслідковому співвідношенні ( I → K ) розподілена в часі його права частина. Відповідно до цієї моделі фіксовані частки {αj} приросту капіталу поточного та наступних років здійснюється за рахунок інвестицій року t. Використання співвідношення (17.72) в економічних моделях ускладнюється тим, що для розрахунку інвестицій поточного року потрібно знати необхідні прирости капіталу наступних Т років. У той же час початкова передумова моделі (17.72) про розподіл у часі інвестицій і приросту капіталу по часовій групі проектів більш реальна, ніж для моделі (17.71).
Моделі (17.71) і (17.72) мають вдвічі менше параметрів, аніж модель (17.70). Однак це число також може бути досить великим. Внаслідок цього виникають проблеми при оцінці параметрів моделі (17.70). Наступним кроком спрощення загальної моделі розподіленого лага є перехід до малопараметричних розподілів.
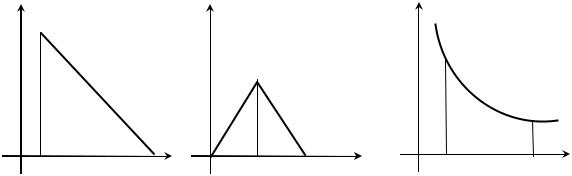
Малопараметричні моделі розподіленого лага. Моделі (17.7017.72) будуть малопараметричними, якщо для них додається умова про конкретний вид розподілу коефіцієнтів {αj} або {βj}. Ці коефіцієнти можуть зростати чи спадати за лінійною, експоненціальною, поліноміальною або будь-якими іншими функціями. Різні автори (Л. Койк, І. Фішер, Д. Лью та інші) пропонували різноманітні коефіцієнти розподілу цих коефіцієнтів. На рис. 17.6.2 представлені типи малопараметричних розподілів лага.
При знаходженні відповідних коефіцієнтів для змішаного, «лівого» чи «правого» розподілів лага необхідно враховувати співвідношення:
T |
T |
|
∑αj |
=1;∑βj |
=1. |
j=1 |
j=1 |
|
592
αj |
αj |
αj |
0 1 2 3 T T+1 j 0 |
K |
T+1 j |
0 1 |
T j |
Рис. 17.6.2. Типи малопараметричних розподілів лага
Розглянемо детальніше одну з малопараметричних моделей, зокрема модель геометричного лага.
Для геометрично розподіленого «лівого» лага прийнято, що в співвідношенні (17.71) коефіцієнти βj є членами нескінченно спадної геометричної прогресії. Знаменник такої прогресії буде 0 < ρ <1, тому
будь-який член |
– |
β |
j |
= β ρj−1 . |
При цьому |
період |
Т |
вважається |
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
=1, |
|
T |
|
|
||
нескінченним. |
Враховуючи, |
що |
∑βj |
маємо |
β∑ρj−1 =1 і, |
|||||||||
|
|
|
|
|
|
|
j=1 |
|
|
j=1 |
|
|||
відповідно, отримуємо: |
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
βj |
= |
|
. |
|
|
|
|
|
||
|
|
|
|
T |
|
|
|
|
|
|
||||
|
|
|
|
|
|
∑ρj−1 |
|
|
|
|
|
|||
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
Скориставшись формулою для визначення суми нескінченно |
||||||||||||||
спадної геометричної прогресії маємо: |
|
|
|
|
|
|||||||||
|
|
|
|
T |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
∑ρj−1 = |
|
|
. |
|
|
|
|
|||
|
|
|
|
1−ρ |
|
|
|
|
||||||
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|||
Звідси, остаточно βj =1−ρ. Тоді з формули (17.77) отримуємо: |
||||||||||||||
Kt = (1−ρ) It +(1−ρ)ρ It−1 +(1−ρ)ρ2 It−2 +…+(1−ρ)ρk It−k +…= |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k −1 |
|
|
(17.73) |
|
|
|
+(1−ρ)ρ It−2 |
+…+(1−ρ)ρ It−k |
= |
|
||||||||
= (1−ρ) It +ρ (1−ρ) It−1 |
+… |
|
||||||||||||
= (1−ρ) It +ρΔKt−1 .
Таким чином, ми отримали однопараметричний розподіл, де ρ – єдиний параметр цього розподілу. В цьому розподілі приріст
капіталу Кt залежить від свого попереднього значення та поточного обсягу інвестицій. Для зручності оцінювання параметра ρ представимо (17.73) так:
It − Kt = ρ(It − Kt−1 ). |
(17.74) |
593
Перетворення (17.74) називають перетворенням Койка. Рівняння (17.74) можна оцінити як рівняння парної лінійної
регресії, вільний член якої рівний нулю. Для цього спочатку по рядах |
|
вихідних даних Іt та Кt розраховуємо такі ряди: |
|
yt = It − Kt , |
|
xt = It − Kt−1 . |
|
При оцінюванні (17.74) виникає проблема специфікації |
|
помилок. Можна припустити, що випадковий член ut у рівнянні |
|
Kt = (1−ρ)It +(1−ρ)ρI1−t +(1−ρ)ρ2 It−2 |
+…+ |
+(1−ρ)ρk It−k +…+ut |
(17.75) |
|
|
задовольняє умови Гауса-Маркова. Після перетворення Койка маємо: |
|
Kt = (1−ρ) It +ρ( Kt−1 −ut−1 )+ut . |
(17.76) |
У рівнянні (17.74) ми отримуємо сукупний випадковий член |
|
ut′ = −ut +ρut−1. Очевидно, що він зв’язаний з пояснювальною змінною ( It − Kt−1 ), оскільки Кt-1 містить ut-1 . Це призводить до порушення
четвертої умови Гауса-Маркова (про статистичну незалежність пояснювальної змінної та випадкового члена). Оцінювання в цьому випадку дасть нам зміщені та неспроможні оцінки.
Існує два шляхи вирішення цієї проблеми.
По-перше. Можна оцінити рівняння (17.75) безпосередньо як рівняння нелінійної регресії. Будь-який сучасний пакет обробки даних дає можливість оцінити таке рівняння, зберігаючи при цьому всі зв’язки між параметрами. Однак у це рівняння можна включити тільки скінченне число членів нескінченного ряду. Зазвичай рекомендується визначити число необхідних членів емпірично (число визначається тоді, коли перестають змінюватися отримувані оцінки). Практично ця рекомендація може застосовуватися тільки для стаціонарних процесів, які продовжуються нескінченно. Дійсно, збільшення числа членів у правій частині рівняння потребує залучення додаткових минулих спостережень пояснювальної змінної або зменшення числа спостережень залежної змінної до моделі. При роботі з реальними даними, тобто з процесами, що відбуваються не зовсім стаціонарно, це призводить до суттєвих змін оцінок на кожному кроці. Такий процес ніколи не закінчується. Таким чином, хороша теоретична рекомендація на практиці не працює.
Другим можливим способом уникнути проблеми можливості порушення умов Гауса-Маркова є припущення про те, що ці умови
594
виконуються не для початкової моделі геометрично розподіленого лага, а для рівняння (17.74). Насправді, може бути так, що умови повністю не виконуються для жодної моделі, але масштаб порушень цих умов незначний і не надто різниться для (17.74) і (17.75). Надалі ми будемо оцінювати перетворені рівняння, вважаючи при цьому, що умови Гауса-Маркова виконуються для рівняння типу (17.74).
Параметр ρ оцінений за формулою (17.74) має задовольняти умову 0 < ρ <1. Автоматично ця умова не є гарантованою, проте
найчастіше вона виконується. Якщо інвестиції перевищують приріст капіталу (Іt> Кt ), то останні зростають, і Кt > Кt-1, і, відповідно, має місце 0< Іt - Кt < Іt - Кt-1 і 0 < ρ <1 в (17.74).
Двопараметрична модель. Існують випадки, при яких загальна тенденція зміни залежної змінної досить добре описана моделлю. Однак при цьому коливання фактичних і розрахункових значень довкола лінії цієї тенденції постійно перебувають у протифазі. Це можна пояснити тим, що однопараметрична геометрична структура лага надто жорстка і не зовсім точно відображає співвідношення вкладу поточних і минулих інвестицій у приріст капіталу. Перехід від однопараметричної до двопараметричної моделі «лівого» геометричного лага дає можливість позбутися такої ситуації. В цій моделі коефіцієнт β1 у виразі (17.71) «відривається» від інших βj, які й надалі створюють нескінченно спадну геометричну прогресію. В результаті цього вираз (17.71) стає таким:
Kt = β1 It +β2 It−1 +β2 ρ It−2 +β2 ρ2 It−3 +… |
+ |
|
|
(17.77) |
||||
+β2 ρk −1 It−k +…. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
Відповідно до перетворень (17.77) маємо: |
|
|
|
|
|
|||
Kt −β1 It = β2 It−1 +β2 ρ It−2 +β2 ρ2 It−3 +…+ |
|
|
|
|
||||
+β2 ρk −1 It−k +…. |
|
Kt−1 −β1 It−1 ). |
|
|
|
|
|
|
|
Kt = β1 It +β2 It−1 +ρ( |
|
|
|
|
(17.78) |
||
|
|
|
|
|
|
∞ |
|
|
При |
цьому необхідне виконання умови |
∑βj =1, |
тобто |
|||||
β1 +β2 (1+ρ+ρ2 +…)=1. |
|
|
|
|
j=1 |
|
|
|
Використавши формулу |
суми |
нескінченно |
||||||
спадної |
геометричної |
прогресії, |
отримуємо |
β + |
β2 |
=1. |
Звідси, |
|
|
|
|
|
1 |
|
ρ |
|
|
β2 = (1−ρ)(1−β1 ). Підставивши значення β2 в (17.78), маємо:
595
Kt = β1 It +(1− ρ)(1− β1 ) It−1 + ρ ( Kt −1 − β1 It−1 )= |
(17.79) |
= β1 It +(1− ρ − β1 ) It−1 − ρ Kt −1. |
|
Після спрощення (17.78) матиме вигляд: |
|
Kt − It−1 = β1 (It − It−1 )+ρ( Kt−1 − It−1 ) . |
(17.80) |
Модель (17.80) містить два параметри 0<β1<1 і 0<ρ<1, тому її називають двопараметричною.
Далі розглянемо модель геометрично розподіленого «правого» лага. Для неї приймаємо, що у співвідношенні (17.72) коефіцієнти αj є членами нескінченно спадної геометричної прогресії, знаменник якої
|
|
∞ |
|
|
ρ. Враховуючи виконання умови ∑αj =1, отримуємо: |
|
|||
|
|
j=1 |
|
|
It = (1− ρ) Kt + ρ(1− ρ) |
Kt+1 + ρ2 (1− ρ) |
Kt+2 +…= |
|
|
= (1− ρ) |
Kt + ρ [(1− ρ) |
Kt+1 + (1− ρ) ρ |
Kt+1 +…]= |
(17.81) |
= (1− ρ) |
Kt + ρ It+1. |
|
|
|
Перетворимо вираз (17.81) у зручну для оцінювання форму: |
||||
|
It − Kt = ρ(It+1 − Kt ). |
|
(17.82) |
|
Дійсно, якщо обсяги інвестицій зростають у часі, то вони більші |
||||
від приростів капіталу, і значення коефіцієнта |
ρ задовольняє умову |
|||
0<ρ<1. Ця умова буде виконуватися і тоді, коли приріст інвестицій спадає в часі, адже при цьому приріст капіталу для відповідних років
спадає ( Kt–It< Kt–It+1).
При оцінюванні рівнянь «правого» розподіленого лага ми не відзначили якихось неточностей. Проте спробуємо перейти від однопараметричної моделі до двопараметричної, як це було здійснено для моделі «лівого» лага. Коефіцієнт α1 у виразі (17.72) «відривається» від інших коефіцієнтів αj. Вони утворюють нескінченно спадну геометричну прогресію. В результаті цих міркувань маємо співвідношення:
It = α1 Kt + α2 Kt+1 + α2ρ Kt+2 |
+ α2ρ2 |
Kt+3 +… |
(17.83) |
Стає очевидним, що |
|
|
|
It −α1 Kt = α2 Kt+1 + α2ρ Kt+2 + α2ρ2 Kt+3 +… |
|
||
∞ |
|
|
|
При цьому з урахуванням умови ∑αj =1 |
отримуємо: |
|
|
j=1 |
|
|
|
It = α1 Kt + (1−ρ)(1−α1 ) Kt+1 +ρ(It+1 −α1 |
Kt+1 ). |
(17.84) |
|
Перетворивши (17.84) до зручного для оцінювання вигляду рівняння лінійної регресії і замінивши (t+1) на t, отримуємо:
596
Kt − It−1 = α1 ( Kt − Kt−1 )+ρ( Kt − It ). |
(17.85) |
Ця модель, як і модель (17.80), буде двопараметричною, оскільки вона містить два параметри (0<α1<1 і 0<ρ<1).
Поліноміальний лаг. Однією з широко відомих моделей розподіленого лага вважається модель поліноміального лагу, інакше лага Алмон. Ідея поліноміального лага полягає в тому, що з допомогою полінома можна апроксимувати поведінку будь-якої функції. Для нашого випадку це означає, що поведінку декількох найважливіших коефіцієнтів розподілу лага (початкових коефіцієнтів) можна описати за допомогою полінома досить малого степеню. Тобто у цьому випадку ми маємо справу з малою кількістю параметрів для оцінювання.
Розглянемо «лівий» розподілений поліноміальний лаг інвестиційного процесу. Його можна записати таким чином:
Kt = α +β0 It +β1It−1 +…+βn It−n +ut . |
(17.86) |
Коефіцієнти β є значеннями полінома степені m: |
|
βs = γ0 + γ1s + γ2 s2 +…+ γm sm . |
(17.87) |
Коефіцієнт β0 буде значенням окресленого полінома при s=0, β1
– при s=1 і т.д. Тут спеціально вводимо вільний член α в рівняння регресії, хоч він уже був включений до загальної моделі інвестиційного лага, і при цьому не вимагаємо виконання умови
∞
∑βj =1. Ці властивості обов’язково мають перевірятися при
j=1
оцінюванні.
Покладемо n=3 i m=2. Тоді |
|
|
|
|
Kt = α + γ0 It + (γ0 + γ1 + γ2 )It−1 |
+ (γ0 + 2γ1 + 4γ2 )It−2 |
+ |
|
|
+ (γ0 +3γ1 +9γ2 )It−3 +ut = α + γ0 |
(It + It−1 |
+ I−2−t + It−3 )+ |
(17.88) |
|
+ γ1 (It−1 + 2I−2−t +3It−3 )+ γ2 (It−1 + 4I−2−t + |
9It−3 )+ut = |
|
||
|
|
|||
= α + γ0 x0 + γ1 x1 + γ2 x2 +ut .
Для того, щоб оцінити параметри моделі вводимо нові змінні: x0 = It + It−1 + It−2 + It−3 ,
x1 = It−1 + 2It−2 +3It−3 ,
x2 = It−1 + 4It−2 +9It−3.
Далі оцінимо параметри α,γ0 ,γ1 ,γ2 і розраховуємо їхні значення:
β0 = γ0 ; |
β2 = γ0 + 2γ1 + 4γ2 ; |
β1 = γ0 + γ1 + γ2 ; |
β3 = γ0 +3γ1 +9γ2 . |
597
17.7. Питання для самоконтролю
1.Дайте визначення часового ряду.
2.Сформулюйте основні задачі, які розв’язуються з допомогою рядів.
3.Охарактеризуйте процедуру прогнозування тренду.
4.Опишіть процедуру кореляційного аналізу часових рядів.
5.Охарактеризуйте основні етапи спектрального аналізу.
6.Призначення методів згладжування та фільтрації, їх основні характеристики.
7.Опишіть основні характеристики авторегресійних моделей.
8.Що являє собою ARIMA, її основні характеристики.
9.Яке призначення методу Фур’є-моделі та його основні кроки?
10.Наведіть приклади економічних задач, для яких при економетричному моделюванні будуть застосовуватися моделі з розподіленим лагом або моделі автокореляції.
11.Яка інтерпретація параметрів моделі з розподіленим лагом? Перерахуйте абсолютні та відносні показники сили зв’язку моделі з розподіленим лагом.
12.Яка інтерпретація параметрів моделі авторегресії? У чому специфіка довготермінового лага в цій моделі?
13.У чому полягає суть методу Алмон? При якій структурі лага його використовують?
14.Опишіть методику застосування підходу Койка при побудові моделі з розподіленим лагом. При якій структурі лага його використовують?
15.У чому суть моделі неповного корегування? Яка методика оцінки її параметрів?
16.У чому суть моделі адаптивних очікувань? Яка методика оцінки її параметрів?
17.Наведіть методику використання методу інструментальних змінних для оцінки параметрів моделі авторегресії.
18.Викладіть методику тестування моделей авторегресії на автокореляцію в залишках. Чому для цього не рекомендують застосовувати критерій Дарбіна-Уотсона?
19.Наведіть основну ідею моделей векторної авторегресії. Які переваги та недоліки цих моделей?
20.У чому суть моделей раціональних очікувань? Яка специфіка оцінки параметрів цих моделей?
598
Розділ 18. Узагальнені економетричні моделі
18.1. Ознаки класифікації економетричних моделей
В економічних дослідженнях, пов’язаних із функціонуванням і розвитком макроекономічних систем, використовуються різноманітні економетричні моделі, які відрізняються цільовим призначенням, характером задачі, ступенем агрегованості, рівнем адекватності, математичним апаратом та ін.
Основною класифікаційною ознакою економетричних моделей є час, згідно з яким моделі діляться на довгострокові, середньострокові та короткострокові. Довгострокові та середньострокові моделі призначені для дослідження найбільш загальних закономірностей економічного росту, виражених з певним ступенем достовірності зміни основних показників розвитку. У результаті отримують усереднену траєкторію, тобто узагальнену тенденцію розвитку деякої системи. Більш детальний розгляд дослідження певного об’єкта можливий на основі дезагрегування моделі, що в свою чергу забезпечить адекватність процесів, які вивчаються. Розклад моделі характеризується збільшенням числа рівнянь і змінних, ускладненням видів зв’язків, форматів функціонування моделі.
Короткотермінові моделі (прогноз до двох років) у цілому спрямовані на визначення тактики стабілізації економіки. Вони повинні правильно передбачати фази циклічного розвитку, зокрема, точки перегину. Короткотермінові моделі мають відображати поточний стан кон’юнктури та найближчі перспективи розвитку економіки, коливання фінансового ринку і стану зовнішньої торгівлі. На сучасному етапі короткотермінові моделі оцінюються в основному на базі квартальної статистичної інформації та підлягають переоцінці через певні інтервали часу.
Відмінною ознакою класифікації короткотермінових моделей (порівняно з довгота середньотерміновими) є відносно висока вимога до формування їх структури, коли значне число змінних переходить у клас позасистемних. У той же час їм, поза сумнівом, властива велика деталізація окремих секторів економіки (наприклад, фінансово-кредитного).
Короткотермінові моделі в основному відображають найбільш рухомі елементи економічної системи, наприклад, попит, і будуються за схемою витрати-дохід-витрати.
599
Довготермінові моделі, як правило, відображають динаміку пропозиції і містять оцінку економічного потенціалу з урахуванням ряду факторів.
Суттєвою класифікаційною ознакою економетричних моделей є принцип вибору екзогенних змінних макроекономічних систем. Введення екзогенних змінних пояснюється природнім обмеженням можливостей моделей і сукупністю питань, які вимагаються при їх побудові.
Виділення множини екзогенних змінних є необхідною умовою навіть у рамках однієї моделі. Дійсно, залежно питань, які ставляться на етапі побудови моделі, одна й та сама змінна може переходити із виду екзогенних у ендогенні і навпаки.
До ендогенних величин системи відносяться і запізнені змінні. За своїм призначенням вони повинні допомагати наближенню дискретного опису моделі до неперервної зміни параметрів реальної економічної системи, тобто забезпечувати стійкий взаємозв’язок у часі як при аналізі окремих змінних, так і при аналізі всієї системи залежностей у цілому, і тим самим надавати моделі динамічного характеру. Використання запізнених змінних дає можливість більш адекватно описати динаміку багатьох характеристик моделі. Так, у більшості економетричних моделях часто використовуються лагові змінні.
Наступна класифікаційна ознака пов’язана з характером взаємозв’язків між змінними у моделях. Більшість моделей мають лінійний або лінеаризований вид рівнянь. Основна перевага лінійних зв’язків полягає в тому, що вони дають можливість оцінити всі рівняння разом, як систему, чого неможливо досягнути при нелінійних рівняннях.
Економетричні моделі також можна класифікувати за ступенем деталізації аналізу економічних систем. Ознака розмірності є нестрогою та вимагає об’єктивної оцінки порогових значень числа зв’язків або змінних моделі. Малорозмірні моделі дозволяють більш наглядно прослідкувати механізм функціонування системи, дають точний прогноз основних характеристик економічного розвитку.
В економетричних моделях великої розмірності складний аналіз параметрів рівнянь. Крім того, в них проходить процес акумуляції помилок, що знижує ступінь достовірності щодо прогнозів, розрахованих за цими моделями.
600
